有M??N 维度的矩阵,将它转化为MN??1的矩阵
import numpy as np
from numpy import squeeze
M, N = 4, 3
h_mat = np.random.randn(M, N)
h_new = squeeze(h_mat.T.reshape(-1, 1))
print(h_new, h_mat, h_new.shape, h_mat.shape)
[-1.06950402 0.57459646 0.41926508 3.20023608 -0.8934199 -1.48817502
-1.46684445 1.04572083 -0.2769263 0.83589263 0.34593235 0.34324631]
[[-1.06950402 -0.8934199 -0.2769263 ]
[ 0.57459646 -1.48817502 0.83589263]
[ 0.41926508 -1.46684445 0.34593235]
[ 3.20023608 1.04572083 0.34324631]]
(12,) (4, 3)
将虚数矩阵转化为实数矩阵
这里m为N*1维矩阵
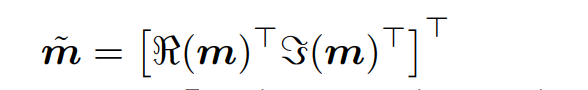
from numpy import real, imag
import numpy as np
mat = np.array([1, 2, 3, -1, -2, -3]) + 1j * np.array([1, 1, 1, 2, 2, 2])
real_mat = squeeze(real(mat).reshape(-1, 1))
img_mat = squeeze(imag(mat).reshape(-1, 1))
all_mat = np.hstack((real_mat, img_mat))
print(mat, "\n", all_mat, "\n", all_mat.shape)
vec_size = int(len(all_mat)/2)
real_part = all_mat[:vec_size,]
img_part = all_mat[vec_size:,]
recon_mat = real_part + 1j * img_part
np.array_equal(mat, recon_mat)
输出:
[ 1.+1.j 2.+1.j 3.+1.j -1.+2.j -2.+2.j -3.+2.j]
[ 1. 2. 3. -1. -2. -3. 1. 1. 1. 2. 2. 2.]
(12,)
True
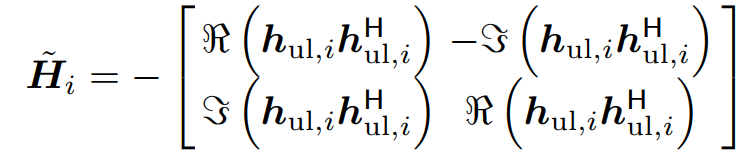
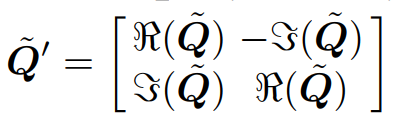
两个类似的,一个负号的区别
import numpy as np
from numpy import real,imag
mat = np.array([1, 2, 3, -1, -2, -3]) + 1j * np.array([1, 1, 1, 2, 2, 2]).reshape(-1,1)
mat = mat * mat.T
real_mat = real(mat)
img_mat = imag(mat)
up = np.hstack((real_mat, -img_mat))
down = np.hstack((img_mat, real_mat))
all_mat = np.vstack((up, down))
print(all_mat)
#%%
mat_size = int(all_mat.shape[0]/2)
real_part = all_mat[:mat_size,:mat_size]
img_part = all_mat[mat_size:,:mat_size]
final_mat = real_part + 1j * img_part
np.array_equal(final_mat, mat)