[人工智能]Learning Spatial Fusion for Single-Shot Object Detection

论文地址：https://arxiv.org/pdf/1911.09516v2.pdf
源码链接：https://github.com/ruinmessi/ASFF
金字塔特征表示是解决目标检测中尺度变化问题的常用方法。然而，不同特征尺度之间的不一致性是基于特征金字塔的检测器的主要限制。在这项工作中，作者提出了一种新的数据驱动的金字塔特征融合策略，称为自适应空间特征融合（ASFF）。它学习了空间过滤冲突信息以抑制不一致性的方法，从而提高了特征的尺度不变性。以解决单级检测器特征金字塔中的不一致性
所提出的方法使网络能够直接学习如何在其他层次上对特征进行空间过滤，从而只保留有用的信息进行组合。对于某一级别的特征，其他级别的特征首先被集成并调整为相同的分辨率，然后进行训练以找到最佳融合。在每个空间位置，不同级别的特征会自适应地融合，也就是说，一些特征可能会被过滤掉，因为它们在该位置携带矛盾的信息，而一些特征可能会以更具辨别力的线索占据主导地位。
ASFF具有以下优点：
（1）由于搜索最优融合的操作是差分的，因此可以方便地在反向传播中学习；
（2） 它与主干模型无关，适用于具有特征金字塔结构的单级探测器；
（3）实现简单，增加的计算量很小。

一、Strong Baseline

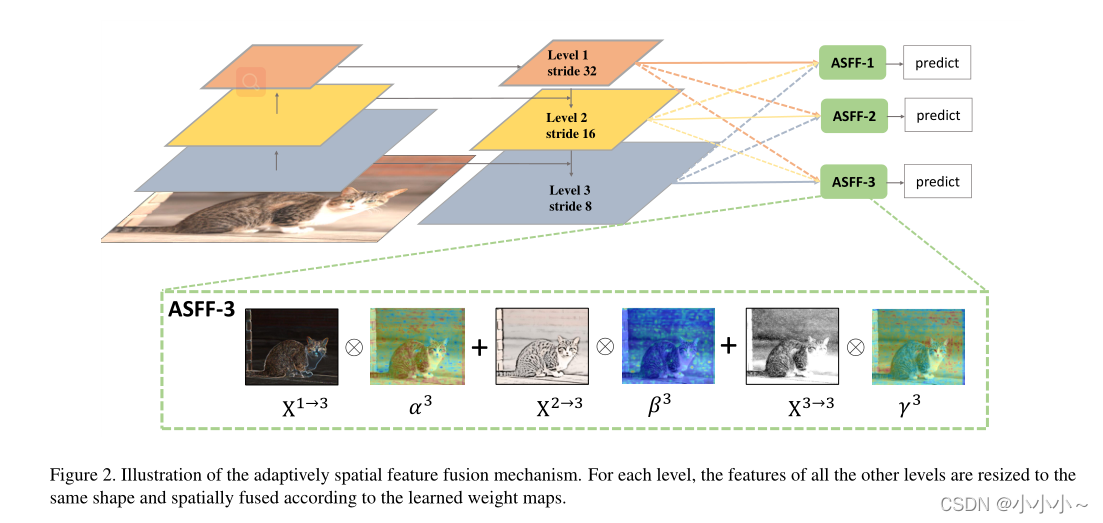
与以往的基于元素求和或级联的多层次特征融合方法不同，本文的关键思想是自适应地学习各尺度特征图融合的空间权重。如↑图所示，它包括两个步骤：相同的尺度缩放和自适应融合。
用$x^l$表示l级分辨率的特征(l∈ {1,2,3}）。对于l级，将另一个n级（N不等于l）的特征$x^n$调整为与$x^l$相同的形状。由于YOLOv3中三个级别的特征具有不同的分辨率和不同的通道数，因此相应地修改了每个级别的上采样和下采样策略。对于上采样，首先使用1×1卷积层将特征的通道数压缩到l级，然后通过插值分别提高分辨率。对于1/2比率的下采样，只需使用3×3卷积层，步幅为2，即可同时修改通道数和分辨率。对于1/4的比例，在步长为2的卷积之前添加了一个步长为2的最大池层。
自适应融合让$x_{ij}^{n\to l}$表示从n级调整到l级的特征图上位置（i，j）处的特征向量。建议在相应的l级融合特征，如下所示：

其中，$y_{ij}^l$表示通道之间输出特征映射yl的第（i，j）个向量。${\alpha }_{ij}^l$、${\beta }_{ij}^l$和${\gamma }_{ij}^l$是三个不同级别到l级别的特征图的空间重要性权重，由网络自适应学习。注意，α和γ都是简单的变量。受的启发，令${\alpha }_{ij}^l$+${\beta }_{ij}^l$+${\gamma }_{ij}^l$=1和${\alpha }_{ij}^l$，${\beta }_{ij}^l$，${\gamma }_{ij}^l$∈ [0,1]，并定义：

这里，${\alpha }_{ij}^l$、${\beta }_{ij}^l$和${\gamma }_{ij}^l$分别以${\lambda }_{{\alpha }_{ij}}^l$、${\lambda }^l{\beta }_{ij}$和${\lambda }_{{\gamma }_{ij}}^l$作为控制参数，通过使用softmax函数来定义。使用1×1卷积层从$x^{1\to l}$、 $x^{2\to l}$和$x^{3\to l}$计算权重标量映射${\lambda }_{\alpha }^l$、${\lambda }_{\beta }^l$和${\lambda }_{\gamma }^l$，因此可以通过标准的反向传播来学习。
通过这种方法，在每个尺度上自适应地聚合所有级别的特征。输出{y1，y2，y3} 用于目标检测.

二、Consistency Property

根据链式规则，ASFF梯度计算如下：

值得注意的是，特征尺寸调整通常使用插值进行上采样，使用池化进行下采样。因此，假设${?}_{x_{ij}}^{1\to l}/{?}_{x_{ij}}^1\approx 1$.为了简单起见。那么等式（3）可以写成：

对于基于金字塔特征的检测器（即元素求和和级联）中使用的两种常见融合操作，可以使用${?}_{y_{ij}}^1/{?}_{x_{ij}}^1=1$和${?}_{x_{ij}}^1/{?}_{x_{ij}}^{1\to l}=1$

假设根据一定的比例匹配机制，将level1处的位置（i，j）指定为对象的中心并且$?L/?y_{ij}^1$是来自阳性样本的梯度。由于相应的位置在其他级别被视为背景，$?L/?y_{ij}^2$和$?L/?y_{ij}^3$是来自负样本的梯度。这种不一致性扰乱了梯度$?L/?y_{ij}^1$并降低原始特征映射$x^1$的训练效率。

处理此问题的一种典型方法是将其他级别的相应位置设置为忽略区域（即。$?L/?y_{ij}^2$=$?L/?y_{ij}^3=0$。然而，尽管$x_{ij}^1$中的冲突已被消除，但$y_{ij}^2$和$y_{ij}^3$的消散往往会导致更差的预测。
对于ASFF，如下所示：

式中${\alpha }_{ij}^1，{\alpha }_{ij}^2，{\alpha }_{ij}^3\in [0,1]$. 利用这三个系数，如果${\alpha }_{ij}^2$→ 0和${\alpha }_{ij}^3$→ 0.由于融合参数可以通过标准的反向传播算法学习，经过良好调整的训练过程可以产生有效系数。同时，监管信息的背景在$y_{ij}^2$和$y_{ij}^3$被保留，避免产生更多误报。

三、参数训练策略

设$\Theta$表示网络参数集（例如卷积滤波器的权重），$\Phi ={\lambda }_{\alpha }^l，{\lambda }_{\beta }^l，{\lambda }_{\gamma }^l|l=1，2，3$是控制每个尺度的空间融合的融合参数集。通过最小化损失函数$L（\Theta ，\Phi$）来联合优化这两组参数，其中$L$是原始YOLOv3目标函数加上anchor shape预测和bounding box回归的IoU回归损失。对DarkNet53的分类预训练应用了 mixup，所有新的卷积层都采用了MSRA权重初始化方法。为了减少过度拟合的风险并提高网络预测的泛化，采用了YOLOv3中的多尺度训练方法。更具体地说，将N个训练图像的小批量调整为N×3×H×W，其中H＝W在{320、352、384、416、448、480、512、544、576、608}中随机选取。
消融实验：


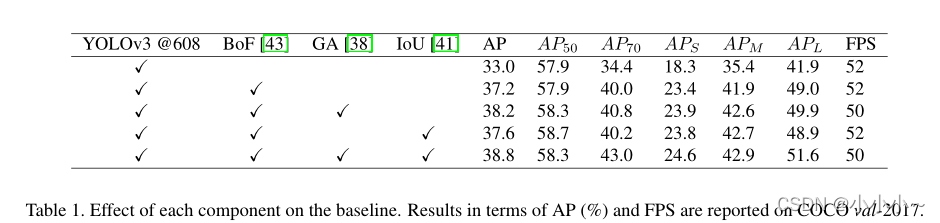
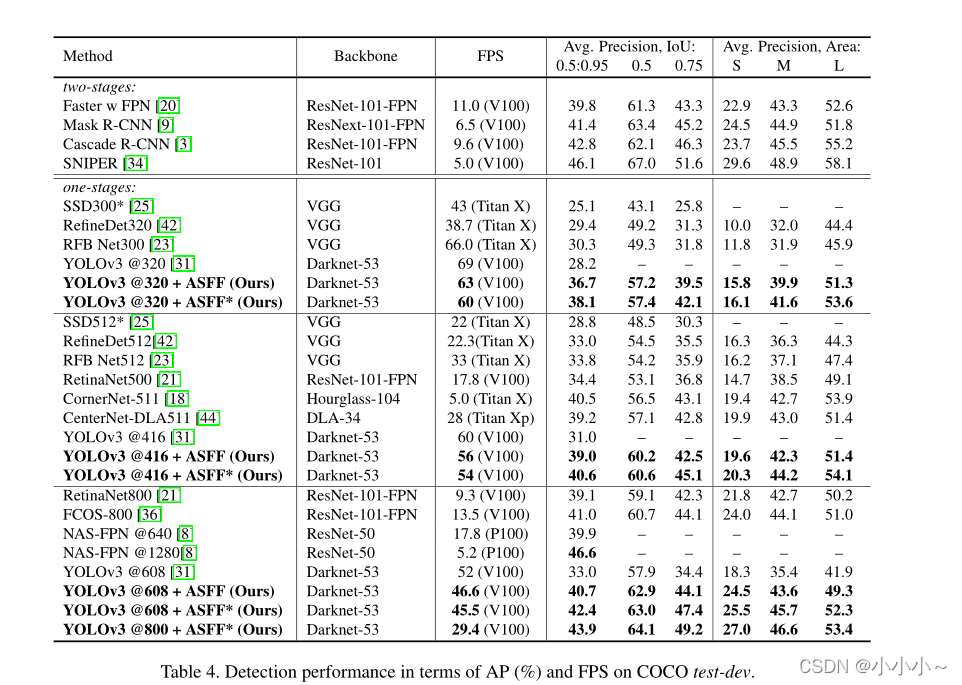
ASSF源码：

class ASFFmobile(nn.Module):
    def __init__(self, level, rfb=False, vis=False):
        super(ASFFmobile, self).__init__()
        # 定义ASSF的尺度级别
        self.level = level
        # 定ASFF不同级别的通道数量
        self.dim = [512, 256, 128]
        # 指定特定级别的通道数量
        self.inter_dim = self.dim[self.level]
        if level==0:
        #先通过3*3步长为2的卷积核进行下采样并且降维后通过3*3的卷积对通道进行调整
            self.stride_level_1 = add_conv(256, self.inter_dim, 3, 2, leaky=False)
            self.stride_level_2 = add_conv(128, self.inter_dim, 3, 2, leaky=False)
            self.expand = add_conv(self.inter_dim, 1024, 3, 1, leaky=False)
        elif level==1:
            self.compress_level_0 = add_conv(512, self.inter_dim, 1, 1, leaky=False)
            self.stride_level_2 = add_conv(128, self.inter_dim, 3, 2, leaky=False)
            self.expand = add_conv(self.inter_dim, 512, 3, 1, leaky=False)
        elif level==2:
            self.compress_level_0 = add_conv(512, self.inter_dim, 1, 1, leaky=False)
            self.compress_level_1 = add_conv(256, self.inter_dim, 1, 1, leaky=False)
            self.expand = add_conv(self.inter_dim, 256, 3, 1,leaky=False)

        compress_c = 8 if rfb else 16  #when adding rfb, we use half number of channels to save memory
		#1*1的卷积为不同等级的权重
        self.weight_level_0 = add_conv(self.inter_dim, compress_c, 1, 1, leaky=False)
        self.weight_level_1 = add_conv(self.inter_dim, compress_c, 1, 1, leaky=False)
        self.weight_level_2 = add_conv(self.inter_dim, compress_c, 1, 1, leaky=False)

        self.weight_levels = nn.Conv2d(compress_c*3, 3, kernel_size=1, stride=1, padding=0)
        self.vis= vis


    def forward(self, x_level_0, x_level_1, x_level_2):
        if self.level==0:
            level_0_resized = x_level_0
            level_1_resized = self.stride_level_1(x_level_1)  #下采样并降低通道

            level_2_downsampled_inter =F.max_pool2d(x_level_2, 3, stride=2, padding=1)  
            level_2_resized = self.stride_level_2(level_2_downsampled_inter)

        elif self.level==1:
            level_0_compressed = self.compress_level_0(x_level_0)
            level_0_resized =F.interpolate(level_0_compressed, scale_factor=2, mode='nearest')
            level_1_resized =x_level_1
            level_2_resized =self.stride_level_2(x_level_2)
        elif self.level==2:
            level_0_compressed = self.compress_level_0(x_level_0)
            level_0_resized =F.interpolate(level_0_compressed, scale_factor=4, mode='nearest')
            level_1_compressed = self.compress_level_1(x_level_1)
            level_1_resized =F.interpolate(level_1_compressed, scale_factor=2, mode='nearest')
            level_2_resized =x_level_2

        level_0_weight_v = self.weight_level_0(level_0_resized)
        level_1_weight_v = self.weight_level_1(level_1_resized)
        level_2_weight_v = self.weight_level_2(level_2_resized)
        levels_weight_v = torch.cat((level_0_weight_v, level_1_weight_v, level_2_weight_v),1)
        levels_weight = self.weight_levels(levels_weight_v)
        levels_weight = F.softmax(levels_weight, dim=1)

        fused_out_reduced = level_0_resized * levels_weight[:,0:1,:,:]+\
                            level_1_resized * levels_weight[:,1:2,:,:]+\
                            level_2_resized * levels_weight[:,2:,:,:]

        out = self.expand(fused_out_reduced)
		#是否对结果进行可视化
        if self.vis:
            return out, levels_weight, fused_out_reduced.sum(dim=1)
        else:
            return out