Introduction

?CNN存在问题：对于变换后输入的编码能力有限，问题出在了Maxpooling方面，使用池化固然可以为网络带来更好的鲁棒性与平移不变性，但这种不变性是以丢失信息为代价的，且随着网络深层的感受野扩大，这种信息的丢失愈发严重。CapsuleNet通过用向量作为基本单位表征实体解决这一问题，向量的模用来表征特征存在的概率，相位用于描述实体特征。CapsuleNet两个关键点是动态路由算法和激活函数的设计，本文试图对它们做出改进：

对于动态路由算法，作者将原本的迭代过程修改为前向传播的卷积，从而加快网络的速度同时保留了空间信息；
CapsuleNet的激活函数有两个重要特质，一是保证了输入向量的角度信息；二是计算时以cap(向量)为基本单位，前人对激活函数的改进都集中在保留角度信息方面，本文则试图从cap-wise性质入手，首先对cap进行仿射变换再进行element-wise的激活，如此丢失角度不变性但保证cap为激活基本单位；

methodology

?首先记胶囊网络中某一层为 $u^l_{w,h,d,n}$ ，其中 $l, w, h$ 为层数和空间尺寸， $d, n$ 描述为每个空间位置上用于描述的胶囊尺寸 $d$ 和通道数 $n$ （感觉这里用 $n$ 个 $d$ 维的胶囊来解释更为准确，因为按照hinton的说法胶囊就是一个向量，不知道本文作者为什么要加入dimension和channle这种描述）， $u^l_{:,:,:,n}$ 表示某个通道的所有胶囊（实际上就是每个空间位置都用一个胶囊描述的情形， $\in R^{w*h*d}$ ），这里定义某个通道所有胶囊是因为后续许多的定义都是同通道胶囊为基本单位。

激活函数

?本文给出的胶囊激活函数如下：
$u^l_{:,:,:,n_0}=tanh(Conv_{1\times1}\ (s^l_{:,:,:,n_0}))$
实质就是对输入的capsule的每个元素进行 $d$ 次线性变换后通过tanh()函数输出，对于每个输入cap该式可以改写为：
$Cap'=Relu([\sum _{i} w^1_iCap_i+b^1,\sum _{i} w^2_iCap_i+b^2],...,\sum _{i} w^1d_iCap_i+b^d])$ .
同时作者假定在同一通道上的所有Cap共享线性变换权重，这就意味着实际上我们只需对输入做 $n$ 次输出通道数为 $d$ 的1*1卷积再通过Relu激活即可得到最终输出。
?作者认为过往研究对于激活函数的改进都过于执着于保证胶囊的方向特征，而对激活函数的基本单位是“向量”这一点视而不见，因此作者以向量的元素为基进行线性变换从而强调这一特性，但也因此丢失原输入向量的方向。同时为了避免胶囊的模值发生较大差异，使用了tanh()函数映入非线性因子的同时将模值限定在合理范围内。直觉上理解的化相当于将胶囊所代表实体的特征进行混合输出，在后续实验中也证明了cap的每个元素的改变都会使得重构图片的某些特征如粗细、角度发生变化，这一理念也是有迹可循的。但为何要同一通道胶囊共享变换参数不是很理解，同一通道并不意味着什么，相反同一空间位置的胶囊共享变换参数反倒更好解释，可能仅仅是为了节省参数？

路由方法

?作者认为原始的路由方法存在着两个重要缺陷，一是参数量过大（应该是指的权重变换矩阵部分），二是使用了迭代过程拖慢计算速度。为此引入了一种attention模式的解决方案。

首先对于 $l ? 1$ 层某个通道的所有Cap我们先计算一次输出通道数为 $D^{l}$ 的卷积以使得胶囊的维度发生变化，得到初始变换后的胶囊值（类似于原始算法中的变换矩阵，但参数共享，conv的概念又和matrix capsule类似）
$\widetilde{s}^{l,n_0}_{(:,:,:,m_0)}=Conv_{3\times3}(u^{l-1}_{(:,:,:,m_0)})$
第 $l$ 层该通道某个位置的胶囊值由相同位置的所有通道的变换后胶囊值加权得到（与原始方法一致）：
$s^l_{(w_0,h_0,:,n_0)}=\sum_{m=1,2,...,N^{l-1}}c^{l,n_0}_{(w_0,h_0,m)}\cdot \widetilde{s}^{l,n_0}_{(w_0,h_0,:,m)}$
权重的获取方式类似于胶囊层面的注意力机制，为了计算底层某空间位置处某个胶囊的权重首先将该一位置的所有胶囊进行拼接，得到 $\widetilde{u}^{l,n_0}_{(w_0,h_0,:,1)}, \widetilde{u}^{l,n_0}_{（w_0,h_0,:,2)},..., \widetilde{u}^{l,n_0}_{(w_0,h_0,:,N^{l-1})}]$ 大小为 $R^{D^{l}\times N^{l-1}}$ 的矩阵，通过与参数矩阵 $W\in R^{D^l\times N^{l-1}}$ 点乘实现初步变换得到初步权重参数 $b^{l,n_0}_{(w_0,h_0,m_0)}$ ，如此计算完该位置所有胶囊的权重后沿着cap通道层面实现权重的归一化获得最终的权重 $C$ 。
同时我们加假定所有位置的参数矩阵是共享的，则这一过程可以简化为对 $U\in R^{W^l\times H^l\times D^l\times N^{l-1}}$ 的输出通道为 $N^{l-1}$ 的 $1\times 1\times D^l$ 3D卷积，公式表示如下：
$b^{l,n_0}_{(:,:,:)}=Conv3D_{1\times1\times D^l}(\widetilde{s}^l_{(:,:,:,:)})\\ c^{l,n_0}_{w_0,h_0,m_0}=\frac{exp(b^{l,n_0}_{(w_0,h_0,m_0)})}{\sum_{1\leq m\leq N^{l-1}}exp(b^{l,n_0}_{w_0,h_0,m})}$
分析这个公式我们可以得到，首先是对每个底层胶囊都需要根据对应相同空间位置的所有胶囊的所有元素计算出权重，然后再执行归一化操作。原始方法同样存在着底层胶囊加权，其目的是类似与聚类一般找到底层胶囊的中心，而由于原始的胶囊经过激活仍然可以保持方向，则我们可以使用底层与当前聚类中心的乘积来衡量二者的相似程度，使得越靠近中心的胶囊具有更高的权重，而聚类中心也在下一次迭代过程中更接近与真实中心。（整体就很类似于K-means聚类的思路）而在本文中，由于激活函数没有保持向量的方向，而且作者想要避免多次迭代拖累运行速度，所以抛弃了聚类中心的理解，选择将底层到顶层的映射视作为了一种参数化的组合，由此使用了参数矩阵 $W$ 作为底层到顶层的路由。直觉上而言，这其实有点背离了hinton的初衷，hinton是认为部件聚合在一起才有可能成为一个更高的实体，而不是组合，失去了这种“邻近”的概念，是否符合胶囊设计的初衷，有待商榷。

模型架构

?模型架构就和原始胶囊网络类似，同样是包含了初始的卷积层，过渡的PriamaryCap层，中间的ConvCap层，最终分类的Fully ConvCap层。损失函数同样是分类Margin loss和L2重构误差作为正则。
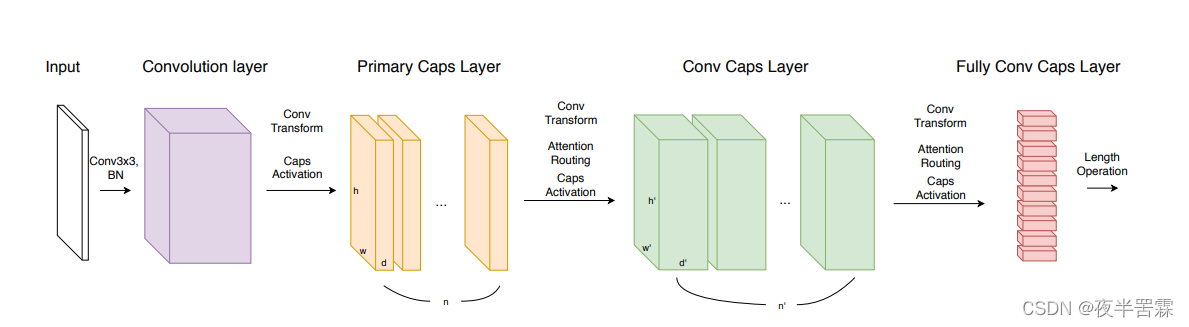
在这里插入图片描述

结果展示

?首先是AR CapsNet在参数更少的情况下与MINIST和CIFA-10分类任务上都取得了比CapSNet更好的结果，同时发现随着Cap层数和维度的增加，网络表现也得到了提升。
?胶囊网络宣称的相对于CNN最显著的改动是在等变性方面，本文同样在这方面进行了验证。

首先是对最后分类Cap的某个元素进行一定程度的扰动（增加或减少），发现重构出的图像随着扰动的逐步变化也在有规律的变化，某些元素的变化会使得重构出数字的角度、粗细等等方面发生变化，说明cap确实能够表征图中实体的某些特征。
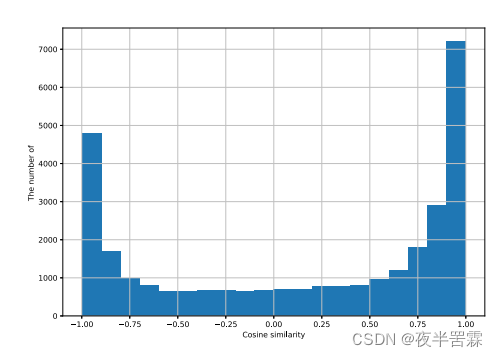
然后是对输入的图像进行了某些仿射变换后再提取最后的胶囊特征，而后对进行相同变换图片得到的特征进行SVD分解得到第一右奇异向量，再计算每个特征和该奇异向量的相关比。发现执行相同变换的图片计算得到的平均相关比呈现出一个较大值，即大家更加的类似，随机变换后图片计算得到的平均相关比则会较小，而且无论模型是在包含或者你不包含autgumention的训练，测试时的平均相关比都很大，从而证明AR capent确实能够将图像的变换体现在最终得到的特征当中。这一结论显然相当的令人振奋，它告诉我们胶囊网路确实满足了它最初的设想。但有个点值得一提，AR capnet似乎并不能分辨出正负变换（指想做或者向右平移这种正负），因为最终相关比的分布显示和奇异向量同方向的特征明显要多余反方向的，见下图，但为什么会这样作者也没有给出解释。