一、背景
神经网络的吸收信息的容量(capacity)受限于参数数目。
条件计算(conditional computation)针对于每个样本,激活网络的部分子网络进行计算,它在理论上已证明,可以作为一种显著增加模型容量的方法。
所以本文引入了稀疏门控专家混合层(Sparsely-Gated Mixture-of-Experts Layer),包括数以千计的前馈子网络。对于每一个样本,有一个可训练的门控网络(gating network)会计算这些专家(指前馈子网络)的稀疏组合。
二、模型结构
本文的条件计算方法,就是引入了一个新的通用神经网络组件类型:稀疏门控专家混合层。
MoE 包含:
- 一些专家,每个专家都是一个简单的前馈神经网络。
- 一个可训练的门控网络,它会挑选专家的一个稀疏组合,用来处理每个输入。
- 所有网络都是使用反向传播联合训练的。
如图所示,我们把 MoE 以卷积的方式(convolutionally)放在多层 LSTM 层之间。在文本的每个位置上,就会调用 MoE 一次,进而可能选择不同的专家组合。不同的专家会倾向于变得高度专业化(基于语法和语义)。



三、平衡专家的利用率
我们观察到,门控网络倾向于收敛到一种不好的状态,即对相同的少量专家,总是会得到较大的权重。这种不平衡是不断自我强化的,随着更好的专家不断训练学习,它们更有可能被门控网络选中。面对这种问题,过去文献有的用硬性约束,有的用软性约束。
而我们采用软性约束方法。我们定义对于一个批次训练样本的专家重要度(the importance of an expert),即该专家在一个批次上的门控输出值的和。并且定义损失项
L
i
m
p
o
r
t
a
n
t
L_{important}
Limportant? ,加入到模型的总损失上。该损失项等于所有专家重要度的方差的平方,再加上一个手工调节的比例因子
w
i
m
p
o
r
t
a
n
t
w_{important}
wimportant?。这个损失项会鼓励所有专家有相同的重要度。
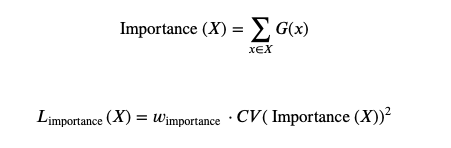
尽管现在的损失函数可以保证相同的重要度,专家仍然可能接收到差异很大的样本数目。例如,某些专家可能接收到少量的大权重的样本;而某些专家可能接收到更多的小权重的样本。为了解决这个问题,我们引入了第二个损失函数:
L
l
o
a
d
L_{load}
Lload? ,它可以保证负载均衡。附录 A 会包含该函数的定义。