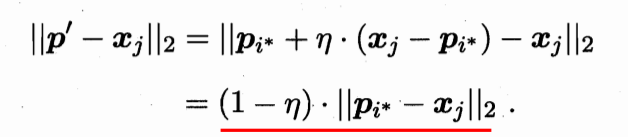1. 聚类任务

（1）目的
聚类试图将样本划分为若干通常不相交的子集。

（2）符号描述

假定样本集 $D=\{x_1,x_2,\cdots,x_m\}$ 包含m个样本。
每个样本 $x_i=\{x_{i1},x_{i,2},\cdots,x_{i,n}\}$ 是一个n维特征向量。
样本被划分为k个不相交的簇 $\{C_l|l=1,2,\cdots,k\}$ 。我们用 $\lambda_j \in \{1,2,\cdots,k\}$ 表示样本 $x_j$ 的簇标记。
因此： $x_j \in C_{\lambda_j}$
聚类结果可以用m个元素的簇标记向量 $\lambda = \{\lambda_1,\lambda_2,\cdots,\lambda_m\}$ 表示

2. 性能度量

（1）目的

正如其名，性能度量能够评估聚类效果的好坏。簇内相似度高、簇间相似度低。
可以将使用的性能度量作为聚类过程的优化目标。

根据是否需要参考模型，可以将指标分为外部指标（external index）和内部指标（internal index）。

2.1 外部指标

标准： 准确率（贴合情况）

对数据集 $D=\{x_1,x_2,\cdots,x_m\}$ 通过聚类给回的簇划分为 $C=\{C_1,C_2,\cdots,C_k\}$ ，参考模型给出的簇划分为 $C^*=\{C^*_1,C^*_2,\cdots,C^*_s\}$ 。令 $\lambda,\lambda^*$ 为对应的样本簇标记向量。
在这里插入图片描述
理解：

a 和 d 表示满足两个样本在 $C$ 获得的簇标签相同（不相同），在 $C^*$ 获得的簇标签也相同（不相同）的数量。
b 和 c 表示满足两个样本在 $C$ 获得的簇标签相同（不相同），在 $C^*$ 获得的簇标签不相同（相同）的数量。
$a+b+c+d=C_2^m=\frac{m(m-1)}{2}$

（1）Jaccard系数
$\frac{a}{a+b+c}$

（2）FM指数
$FMI=\sqrt{\frac{a}{a+b} \times \frac{a}{a+c}}$

（3）Rand指数
$RI=\frac{2(a+d)}{m(m-1)}$

上述三种指数可以表示在 $C,C^*$ 均划分为相同簇的样本对的数量的总量占比。
取值范围为 $[0, 1]$ ，值越大越好。值越大表示聚类越贴合实际情况，划分正确率越高。

2.2 内部指标

标准： 簇内相似度高、簇间相似度低
定义四个簇划分指标，再利用指标度量内部指标。

簇内样本的平均距离
$\frac{2}{|C|(|C-1|)} \sum_{1 \leq i \leq j \leq |C|}dist(x_i,x_j)$
簇内样本的最远距离
$\max_{1 \leq i \leq j \leq |C|} dist(x_i,x_j)$
簇间样本的最短距离
$d_{min}(C_i,C_j) = \min_{x_i \in C_i,x_j \in C_j} dist(x_i,x_j)$
簇间中心点的距离
$d_{cen}(C_i,C_j) = dist(\mu_i,\mu_j)$

（1）DB指数（DBI）
$DBI=\frac{1}{k} \sum_{i=1}^k \max_{j \neq i} \frac{avg(C_i)+avg(C_j)}{d_{cen}(C_i,C_j)}$

DBI值越小，表示簇内越紧密，簇间越分散。

（2）Dunn指数（DI）
$\min_{1 \leq i \leq k} \{\min_{j \neq i}(\frac{d_{min}(C_i,C_j)}{\max_{1 \leq l \leq k}diam(C_l)}) \}$

DI值越大，表示簇内越紧密，簇间越分散。

3. 距离计算

我们通过距离来定义相似度度量。
（1）基本性质
在这里插入图片描述

3.1 有序属性

举例：{1, 2, 3}中1与2比1与3接近。可以根据次序进行距离度量
（1）闵可夫斯基距离
在这里插入图片描述

当P=1时，变成曼哈顿距离
$dist(x_i,x_j) = \sum_{u=1}^n |x_{iu}-x_{ju}|$
当P=2时，变成欧氏距离
$dist(x_i,x_j) =\sqrt{ \sum_{u=1}^n |x_{iu}-x_{ju}|^2}$

3.2 无序属性

举例：{飞机，火车，轮船}中没办法按照次序进行距离度量。
（1）VDM
令 $m_{u,a}$ 表示属性u上取值为a的样本数， $m_{u,a,i}$ 表示在第i个簇中属性u上取值为a的样本数。则a,b两个离散属性的VDM距离为：
$VDM_p(a,b) = \sum_{i=1}^k |\frac{m_{u,a,i}}{m_{u,a}}-\frac{m_{u,b,i}}{m_{u,b}}|^p$

理解：无序属性距离的计算需要提前知道簇划分吗？

3.3 混合属性

假设前 $n_c$ 个为有序属性，后面为无需属性。
在这里插入图片描述

4. 原型聚类

4.1 k-means

未知标签类型的聚类划分。
均值向量、样本划分

（1）优化目标
在这里插入图片描述
解决上述目标为NP难问题，因此通过迭代优化近似求解。

（2）算法
在这里插入图片描述

随机选择k个样本作为中心
根据样本与选择中心点的距离，划分样本的类别
计算簇内均值向量，当向量改变时将新的均值向量作为新簇的中心。当不在更新或到达最大轮数或最小调整阈值时退出循环。

理解： 通过最小化簇内均值选择聚合中心位置。

4.2 学习向量量化（LVQ）

需要预知标签类型，用监督信息辅助聚类。
原型向量、拉近远离

（1）优化目标
对于任意样本x,它将被划入距离最近的原形向量所代表的簇中。需要使标记相同的靠拢，标记不同的远离。
$p'=p_{i^*} + \eta \times (x_j-p_{i^*}) \ 靠近 \\ p'=p_{i^*} - \eta \times (x_j-p_{i^*}) \ 远离 \\ p_{i^*} = p'$