[人工智能]推荐算法之--矩阵分解(Matrix Factorization)

推荐算法之–矩阵分解(Matrix Factorization)

在众多推荐算法或模型的发展演化脉络中，基于矩阵分解的推荐算法，处在了一个关键的位置：

• 向前承接了协同率波的主要思想，一定程度上提高了处理稀疏数据的能力和模型泛化能力，缓解了头部效应；
• 向后可以作为Embedding思想的一种简单实现，可以很方便、灵活地扩展为更加复杂的深度学习模型。

因此，矩阵分解模型虽然简单，但也值得深入理解和思考。

1. 共现矩阵

推荐问题中，不同人对不同物品的倾向/喜欢程度，可表示为共现矩阵，即记录某个人和某个物品共同出现的 频次/频率/概率。

例如，商品推荐|新闻推荐|视频推荐 场景中，矩阵第u行第i列的元素，可以表示第u个人对第i个商品|新闻|视频 的 购买次数|点击次数|观看时长。

直观地，假设有5个用户，5个商品，根据是否存在购买行为（买过为1，否则0），可表示为共现矩阵$Y_{gt}$：

Y_gt = [1, 1, 1, 0, 0], # 用户1
       [1, 1, 1, 0, 0], # 用户2
       [1, 1, 1, 0, 0], # 用户3
       [0, 0, 0, 1, 1], # 用户4
       [0, 0, 0, 1, 1], # 用户5

其中每一行对应一个用户，每一列对应一个商品，即用户123买过商品123，用户45买过商品45。

上面的矩阵中，所有元素都是已知的，然而实际场景中，仅有少数元素是已知的，大部分位置是空缺和未知的，例如，几乎没有人买过某宝/某东商品列表中的所有商品。

因此，推荐算法的应用场景，则是对上述矩阵中存在的未知元素进行预测，例如电商场景中，预测某个用户对某个商品的购买倾向。

一个简单的例子，从上面的矩阵$Y_{gt}$中“挖去”一些元素，得到如下矩阵$Y$，其中问号“？”表示待估计值；

Y = [1, 1, 1, 0, ?], # 用户1
    [1, 1, 1, ?, 0], # 用户2
    [1, 1, ?, 0, 0], # 用户3
    [0, ?, 0, 1, 1], # 用户4
    [?, 0, 0, 1, 1], # 用户5

2. 矩阵分解

“物以类聚，人以群分”，购买过相同物品的人，往往有着相同的购买倾向或兴趣。

例如，根据有“空洞”的共现矩阵$Y$，用户123都买过物品12，有着相同的购买倾向，同时用户12都买过物品3，于是可以推测用户3可能也会喜欢物品3.

人群的“兴趣模式”，通常少于人的个数或物品的个数，且随着人数和物品数量的增多，这种效果会越来越明显，即人群的“兴趣模式”是稀疏的；

从矩阵的角度，也不难看出，对于上面的例子，矩阵$Y_{gt}$的秩只有2，小于矩阵的行数/列数，即矩阵中存在着大量冗余信息。

从谱分析的角度，矩阵分解模型相当于一个低通滤波器：通过对共现矩阵进行低秩分解，滤掉了低能量的高频信息，保留了高能量的低频信息。

3. SVD实现矩阵分解

对于小型矩阵，通过SVD的方式可简单实现矩阵分解。然而，此类方式存在一些问题：

1. 不适用于大矩阵，容易爆内存；
2. 需要预先对缺失值进行填充；
3. 缺失值填充后会和已知数据混淆，不能区分开。

一个简单的例子如下：

import numpy as np
# 参数
num_user = 5     # 用户个数
num_item = 5     # 商品个数
latent   = 2     # 隐向量维度(Embedding)
## Y_gt
Y_gt = np.array([
    [1, 1, 1, 0, 0],
    [1, 1, 1, 0, 0],
    [1, 1, 1, 0, 0],
    [0, 0, 0, 1, 1],
    [0, 0, 0, 1, 1],
], dtype=np.float)
# Y
Y = Y_gt.copy()
Y[0, 4] = Y[1, 3] = Y[2, 2] = Y[3, 1] = Y[4, 0] = None
# 填充为0.5
Y_padding = np.nan_to_num(Y, nan=0.5)
# SVD分解
U, S, Vh = np.linalg.svd(Y_padding, full_matrices=True)
# 把奇异值S平分到用户矩阵P和物品矩阵Q上
P = U[:, :latent] * np.sqrt(S[:latent]).reshape(1, -1)
Q = Vh[:latent, :]* np.sqrt(S[:latent]).reshape(-1, 1)
## 最终得到的 用户矩阵P、物品矩阵Q
print('P = \n', np.around(P,2))
print('Q = \n', np.around(Q,2))
# 对Y进行重建，实现缺失值估计
Y_re = P @ Q
# -------------------------------------输出结果
# P = 
#  [[-0.99  0.27]   # 用户/物品隐向量的 几何特征；
#  [-0.99  0.27]    # 用户123 & 物品123，隐向量基本同向，内积≈1；
#  [-0.78  0.4 ]    # 用户45  & 物品45 ，隐向量基本同向，内积≈1；
#  [-0.48 -0.88]    # 用户123 & 物品45 , 隐向量基本正交，内积≈0；
#  [-0.48 -0.88]]   # 用户45  & 物品123, 隐向量基本正交，内积≈0；
# Q = 
#  [[-0.99 -0.99 -0.78 -0.48 -0.48]
#  [ 0.27  0.27  0.4  -0.88 -0.88]]
# -------------------------------------

这里准备一个作图的函数，简化代码，方便展示结果，后面还会用到：

import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = 'SimHei'
def show_result(curve, curve_name, Y, Y_re, figname, save=False):
    fig, axs = plt.subplots(1, 3, figsize=(15, 5), num=figname)
    axs[0].plot(curve)              # 曲线
    axs[0].grid()
    axs[0].set_title(curve_name)
    axs[1].imshow(Y, cmap='gray')   # 待预测/填充数据
    axs[1].set_title('待填充数据')
    axs[2].imshow(Y_re, cmap='gray')# 填充/预测结果
    axs[2].set_title('预测填充')
    for u in range(num_user):
        for i in range(num_item):
            if np.isnan(Y[u,i]):
                axs[1].text(u-0.1, i+0.1, '?', fontsize=20, color='r')
                axs[2].text(u-0.25, i+0.1, '%1.2f'%Y_re[u,i], fontsize=12, color='r')
            else:
                axs[1].text(u-0.2, i+0.1, str(Y[u,i]), fontsize=12, color='g')
                axs[2].text(u-0.25, i+0.1, '%1.2f'%Y_re[u,i], fontsize=12, color='g')
    if save:
        fig.savefig('./image/%s.png'%(figname))

调用作图函数，展示结果：

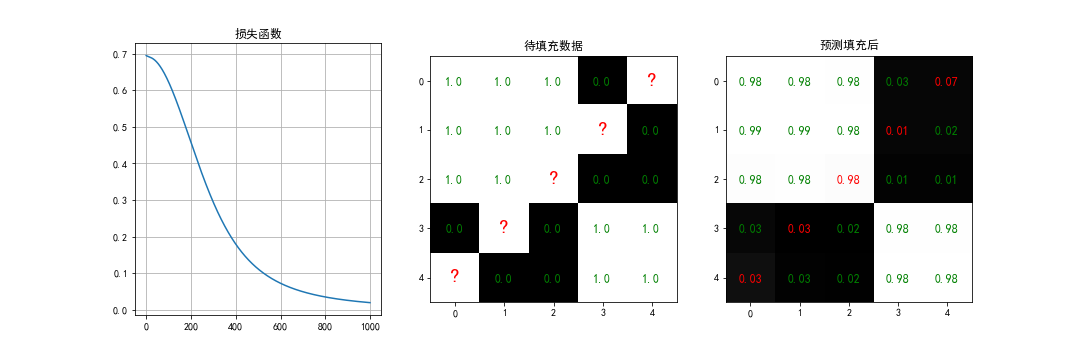
show_result(curve=S, curve_name='奇异值', Y=Y, Y_re=Y_re, figname='SVD', save=True)

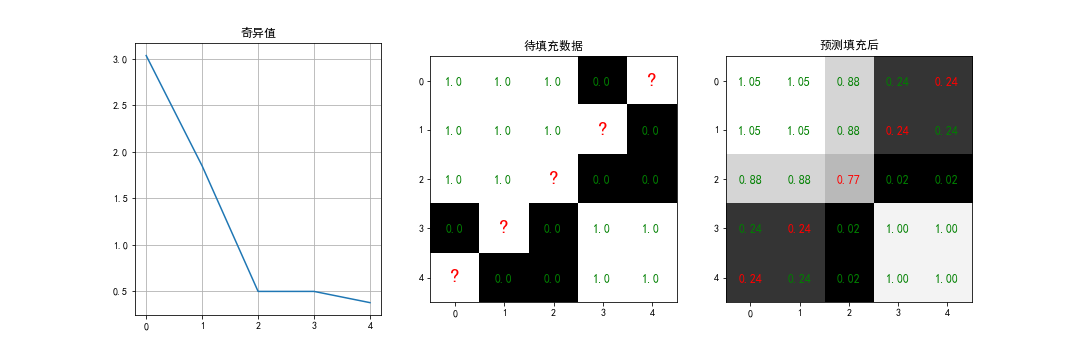
可以看到，SVD后，只有两个较大奇异值，因此信息大多保留在 左/右奇异矩阵的前 2列/行中。丢掉 左/右奇异矩阵的 后3列/行，实现了低通滤波和数据重建；

4. 梯度下降

因为SVD求解时存在的问题，实际场景中一般不用SVD，而是采用数值迭代和梯度下降的方式，实现矩阵分解。

同时，可以为用户、物品、和用户-物品整体 各添加偏置项（有点类似batch normalization的作用），让被分解对象尽量有0均值，降低模型复杂度。

4.1 前向推理 & 符号表示

对于共现矩阵$Y$的第$u$行第$i$列，即第$u$个用户对第$i$个物品的 点击率/购买概率，将模型对它的估计值记作${\hat{y}}_{u,i}$：

$${\hat{y}}_{u,i}=\sum _{k=0}^K{P}_{u,k}?Q_{k,i}+p_u+q_i+c$$

其中，待求解的参数集合 Θ = { P , Q , p , q , c } \Theta= \{ P, Q, p, q, c \} Θ={P,Q,p,q,c}：

$P$ – 用户矩阵，共M行K列，M为用户个数。$P_{u,k}$表示其第$u$行第$k$列的元素；
$Q$ – 物品矩阵，共K行N列，N为物品个数，$Q_{k,i}$表示其第$k$行第$i$列的元素；
$p$ – 用户偏置向量，共M个元素；
$q$ – 物品偏置向量，共N个元素；
$c$ – 整体偏置，标量；
$K$ – 相当于Embeding / 隐向量维度，通常$K$远小于$M,N$；

4.2 损失函数

以$y_{u,i}$为真值(Ground Truth)，误差损失（MSE）：

$$L_e=\Vert \hat{y}?y{\Vert }^2=\sum _{u,i}({\hat{y}}_{u,i}?y_{u,i}{)}^2$$

正则化损失：

$$L_2=\Vert P{\Vert }^2+\Vert Q{\Vert }^2+\Vert p{\Vert }^2+\Vert q{\Vert }^2+\Vert c{\Vert }^2$$

综上，整体损失

$$L=L_e+\lambda L_2$$

4.3 梯度计算

关于损失误差$L_e$：

$$\begin{array}{rl}\frac{?L_e}{?{\hat{y}}_{u,i}}& =2({\hat{y}}_{u,i}?y_{u,i})\\ \frac{?{\hat{y}}_{u,i}}{?P_{u,k}}& =Q_{k,i}\\ \frac{?{\hat{y}}_{u,i}}{?Q_{k,i}}& =P_{u,k}\\ \frac{?{\hat{y}}_{u,i}}{?p_u}& =\frac{?{\hat{y}}_{u,i}}{?q_i}=\frac{?{\hat{y}}_{u,i}}{?c}=1\end{array}$$

于是有：

$$\begin{array}{rl}\frac{?L_e}{?P_{u,k}}& =\frac{?L_e}{?{\hat{y}}_{u,i}}\frac{?{\hat{y}}_{u,i}}{?P_{u,k}}=2({\hat{y}}_{u,i}?y_{u,i})Q_{k,i}\\ \frac{?L_e}{?Q_{k,i}}& =\frac{?L_e}{?{\hat{y}}_{u,i}}\frac{?{\hat{y}}_{u,i}}{?Q_{k,i}}=2({\hat{y}}_{u,i}?y_{u,i})P_{u,k}\\ \frac{?L_e}{?p_u}& =\frac{?L_e}{?{\hat{y}}_{u,i}}\frac{?{\hat{y}}_{u,i}}{?p_u}=2({\hat{y}}_{u,i}?y_{u,i})\\ \frac{?L_e}{?q_i}& =\frac{?L_e}{?{\hat{y}}_{u,i}}\frac{?{\hat{y}}_{u,i}}{?q_i}=2({\hat{y}}_{u,i}?y_{u,i})\\ \frac{?L_e}{?c}& =\frac{?L_e}{?{\hat{y}}_{u,i}}\frac{?{\hat{y}}_{u,i}}{?c}=2({\hat{y}}_{u,i}?y_{u,i})\end{array}$$

关于正则误差$L_2$

$$\begin{array}{rl}\frac{?L_2}{?P_{u,k}}& =2P_{u,k}\\ \frac{?L_2}{?Q_{k,i}}& =2Q_{k,i}\\ \frac{?L_2}{?p_u}& =2p_u\\ \frac{?L_2}{?q_i}& =2q_i\\ \frac{?L_2}{?c}& =2c\end{array}$$

综上，整体梯度：

$$\frac{?L}{?\theta }=\frac{?L_e}{?\theta }+\lambda \frac{?L_2}{?\theta }$$

其中，$\theta \in \Theta$ 表示参数集合 Θ = { P , Q , p , q , c } \Theta= \{ P, Q, p, q, c \} Θ={P,Q,p,q,c} 中每个参数；

4.4 代码测试

首先准备数据集，将上面的共现矩阵$Y$，转换为$(u?i?y_{u,i})$三元组的形式，保存为DataFrame.

## 数据集
import pandas as pd
dataset = pd.DataFrame(columns=['user', 'item', 'score'])
for u in range(num_user):
    for i in range(num_item):
        if np.isnan(Y[u,i]):
            continue
        dataset = dataset.append({
                    'user'   : u,
                    'item'   : i,
                    'score'  : Y[u,i]
                }, ignore_index=True)
print(dataset)

准备好的数据集（5×5的矩阵，除去5个缺失值，还剩20条数据）：

    user  item  score
0    0.0   0.0    1.0
1    0.0   1.0    1.0
2    0.0   2.0    1.0
3    0.0   3.0    0.0
4    1.0   0.0    1.0
5    1.0   1.0    1.0
6    1.0   2.0    1.0
7    1.0   4.0    0.0
8    2.0   0.0    1.0
9    2.0   1.0    1.0
10   2.0   3.0    0.0
11   2.0   4.0    0.0
12   3.0   0.0    0.0
13   3.0   2.0    0.0
14   3.0   3.0    1.0
15   3.0   4.0    1.0
16   4.0   1.0    0.0
17   4.0   2.0    0.0
18   4.0   3.0    1.0
19   4.0   4.0    1.0

为了简化代码，创建两个函数，后面还会用到：

# 初始化模型参数
def initial_para():
    P = np.random.randn(num_user, latent) * 0.01      # 用户矩阵
    Q = np.random.randn(latent, num_item) * 0.01      # 商品矩阵
    p = np.zeros(num_user, dtype=np.float)            # 用户偏置
    q = np.zeros(num_item, dtype=np.float)            # 商品偏置
    c  = 0.0                                          # 整体偏置
    return P, Q, p, q, c
## 打印模型参数
def print_para(P=None, Q=None, p=None, q=None, c=None):
    if P is not None:   print('P = \n', np.around(P,2))
    if Q is not None:   print('Q = \n', np.around(Q,2))
    if p is not None:   print('p = ',   np.around(p,2))
    if q is not None:   print('q = ',   np.around(q,2))
    if c is not None:   print('c = ',   np.around(c,2))

正式开始模型训练：

lr          = 1e-2      # 学习率
lambda_l2   = 1e-2      # 正则化参数
num_epoch   = 500       # 迭代次数
loss        = []        # 记录loss
P, Q, p, q, c = initial_para()          # 初始化模型参数
idx_shuffle = np.arange(len(dataset))   # 训练数据序号，后面会乱序读取
for epoch in range(num_epoch):
    loss_err = 0.0
    np.random.shuffle(idx_shuffle)      # 打乱训练集序号顺序
    for idx in idx_shuffle:
        u = int(dataset.iloc[idx]['user'])
        i = int(dataset.iloc[idx]['item'])
        gt =    dataset.iloc[idx]['score']
        # 前向传播
        score = np.dot(P[u, :], Q[:, i]) + p[u] + q[i] + c
        eui = score - gt
        # 误差损失（均方误差） 
        loss_err += eui ** 2
        # 反向传播，梯度下降        
        P[u, :] -= lr * (2 * eui * Q[:, i] + 2 * lambda_l2 * P[u, :] )
        Q[:, i] -= lr * (2 * eui * P[u, :] + 2 * lambda_l2 * Q[:, i] )
        p[u]    -= lr * (2 * eui           + 2 * lambda_l2 * p[u]    )
        q[i]    -= lr * (2 * eui           + 2 * lambda_l2 * q[i]    )
        c       -= lr * (2 * eui           + 2 * lambda_l2 * c       )
    # L2正则化误差
    loss_l2 = lambda_l2 * np.linalg.norm(P, ord=2) + \
              lambda_l2 * np.linalg.norm(Q, ord=2) + \
              lambda_l2 * np.linalg.norm(p, ord=2) + \
              lambda_l2 * np.linalg.norm(q, ord=2) + \
              lambda_l2 * np.abs(c)
    loss.append(loss_err + loss_l2)
    if epoch % 100 == 0:
        print('Epoch=%03d, Loss=%1.6f, L2=%1.6f, lr=%1.6f'%(epoch, loss_err, loss_l2, lr))

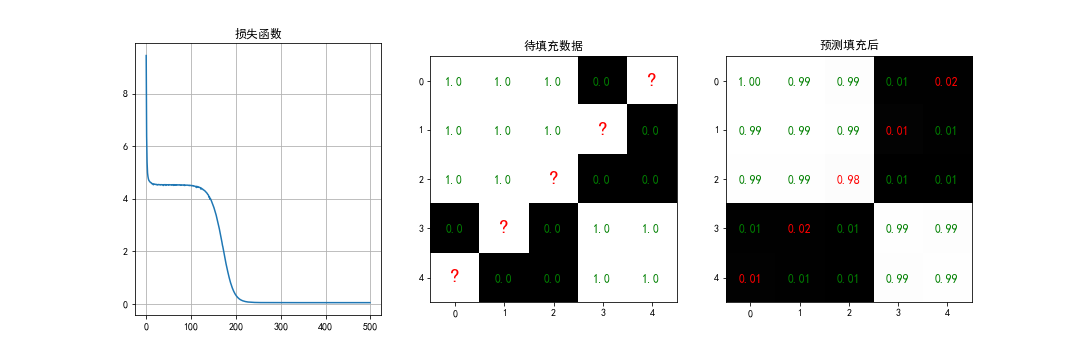
模型训练完成后，对存在缺失元素的共线矩阵$Y$进行重建/填充，实现缺失值预测。并展示结果。

# 预测填充
Y_re = np.matmul(P, Q) + p.reshape((-1, 1)) + q.reshape((1, -1)) + c

## 结果展示
print_para(P, Q, p, q, c)
show_result(curve=loss, curve_name='损失函数', Y=Y, Y_re=Y_re, figname='SGD_linear', save=True)
# -------------------------------------输出结果
# P = 
#  [[ 0.18  0.55]   # 用户/物品 隐向量的 几何特征：
#  [ 0.2   0.55]    # 用户123 & 物品123，隐向量基本同向；
#  [ 0.18  0.55]    # 用户45  & 物品45 ，隐向量基本同向；
#  [-0.28 -0.77]    # 用户123 & 物品45 , 隐向量基本反向；
#  [-0.25 -0.78]]   # 用户45  & 物品123, 隐向量基本反向；
# Q = 
#  [[ 0.19  0.17  0.19 -0.26 -0.28]
#  [ 0.55  0.56  0.55 -0.78 -0.77]]
# p =  [0.2  0.2  0.2  0.03 0.03]
# q =  [0.2  0.2  0.2  0.03 0.03]
# c =  0.25

5. 梯度下降 + sigmoid：

上面的预测模型，并未对输出结果进行规范化，即将最终概率限制到0~1。

当然也可以得到预测结果后，在后面手动添加一个限制函数：

$$f(x)=\text{min}[1,\text{max}(0,x)]$$

这里尝试另一种思路，即在模型结构输出端添加sigmoid函数，让用户/物品矩阵学会适应sigmoid的非线性效果，端到端地训练模型，不对模型输出的结果做二次处理。

5.1 前向推理 & 符号表示

添加sigmoid层后，模型输出${\hat{y}}_{u,i}$变成了：

$$\begin{array}{rl}{o}_{u,i}& =\sum _{k=0}^K{P}_{u,k}?Q_{k,i}+p_u+q_i+c\\ {\hat{y}}_{u,i}& =\text{sigmoid}(o_{u,i})\end{array}$$

5.2 损失函数

误差损失（用交叉熵，和sigmoid搭配，保证梯度合理）：

$$L_e=?\sum _{u,i}[y_{u,i}?\text{log}({\hat{y}}_{u,i})+(1?y_{u,i})?\text{log}(1?{\hat{y}}_{u,i})]$$

正则化损失同4.2节，略。

综上，整体损失（同4.2节）：

$$L=L_e+\lambda L_2$$

5.3 梯度计算

关于损失误差$L_e$：

$$\begin{array}{rl}\frac{?L_e}{?{\hat{y}}_{u,i}}& =\frac{{\hat{y}}_{u,i}?y_{u,i}}{{\hat{y}}_{u,i}(1?{\hat{y}}_{u,i})}\\ \frac{?{\hat{y}}_{u,i}}{?o_{u,i}}& ={\hat{y}}_{u,i}(1?{\hat{y}}_{u,i})\end{array}$$

于是可简化为：

$$\frac{?L_e}{?o_{u,i}}={\hat{y}}_{u,i}?y_{u,i}$$

此外，类比4.3节：
$$\begin{array}{rl}\frac{?o_{u,i}}{?P_{u,k}}& =Q_{k,i}\\ \frac{?o_{u,i}}{?Q_{k,i}}& =P_{u,k}\\ \frac{?o_{u,i}}{?p_u}& =\frac{?o_{u,i}}{?q_i}=\frac{?o_{u,i}}{?c}=1\end{array}$$

于是有：

$$\begin{array}{rl}\frac{?L_e}{?P_{u,k}}& =\frac{?L_e}{?o_{u,i}}\frac{?o_{u,i}}{?P_{u,k}}=({\hat{y}}_{u,i}?y_{u,i})Q_{k,i}\\ \frac{?L_e}{?Q_{k,i}}& =\frac{?L_e}{?o_{u,i}}\frac{?o_{u,i}}{?Q_{k,i}}=({\hat{y}}_{u,i}?y_{u,i})P_{u,k}\\ \frac{?L_e}{?p_u}& =\frac{?L_e}{?o_{u,i}}\frac{?o_{u,i}}{?p_u}=({\hat{y}}_{u,i}?y_{u,i})\\ \frac{?L_e}{?q_i}& =\frac{?L_e}{?o_{u,i}}\frac{?o_{u,i}}{?q_i}=({\hat{y}}_{u,i}?y_{u,i})\\ \frac{?L_e}{?c}& =\frac{?L_e}{?o_{u,i}}\frac{?o_{u,i}}{?c}=({\hat{y}}_{u,i}?y_{u,i})\end{array}$$

正则误差$L_2$和同4.3节相同，略。

综上，整体梯度：

$$\frac{?L}{?\theta }=\frac{?L_e}{?\theta }+\lambda \frac{?L_2}{?\theta }$$

其中，$\theta \in \Theta$ 表示参数集合 Θ = { P , Q , p , q , c } \Theta= \{ P, Q, p, q, c \} Θ={P,Q,p,q,c} 中每个参数；

5.4 代码测试

模型训练：

## ================
def sigmoid(x):
    return np.exp(x) / (1 + np.exp(x))
## ================
lr          = 1e-2
lambda_l2   = 1e-2
num_epoch   = 1000
loss        = []
P, Q, p, q, c = initial_para()
idx_shuffle = np.arange(len(dataset))
for epoch in range(num_epoch):
    loss_err = 0.0
    np.random.shuffle(idx_shuffle)
    for idx in idx_shuffle:
        u = int(dataset.iloc[idx]['user'])
        i = int(dataset.iloc[idx]['item'])
        gt =    dataset.iloc[idx]['score']
        # 前向传播
        y = np.dot(P[u, :], Q[:, i]) + p[u] + q[i] + c
        score = sigmoid(y)
        # 误差损失（交叉熵） 
        loss_err += -(gt * np.log(score + 1e-8) + (1 - gt) * np.log(1 - score + 1e-8))
        # 反向传播，梯度下降
        eui = score - gt
        P[u, :] -= lr * (eui * Q[:, i] + 2 * lambda_l2 * P[u, :] )
        Q[:, i] -= lr * (eui * P[u, :] + 2 * lambda_l2 * Q[:, i] )
        p[u]    -= lr * (eui           + 2 * lambda_l2 * p[u]    )
        q[i]    -= lr * (eui           + 2 * lambda_l2 * q[i]    )
        c       -= lr * (eui           + 2 * lambda_l2 * c       )
    loss_l2 = lambda_l2 * np.linalg.norm(P, ord=2) + \
              lambda_l2 * np.linalg.norm(Q, ord=2) + \
              lambda_l2 * np.linalg.norm(p, ord=2) + \
              lambda_l2 * np.linalg.norm(q, ord=2) + \
              lambda_l2 * np.abs(c)
    loss.append(loss_err + loss_l2)
    if epoch % 100 == 0:
        print('Epoch=%03d, Loss=%1.6f, L2=%1.6f, lr=%1.6f'%(epoch, loss_err, loss_l2, lr))

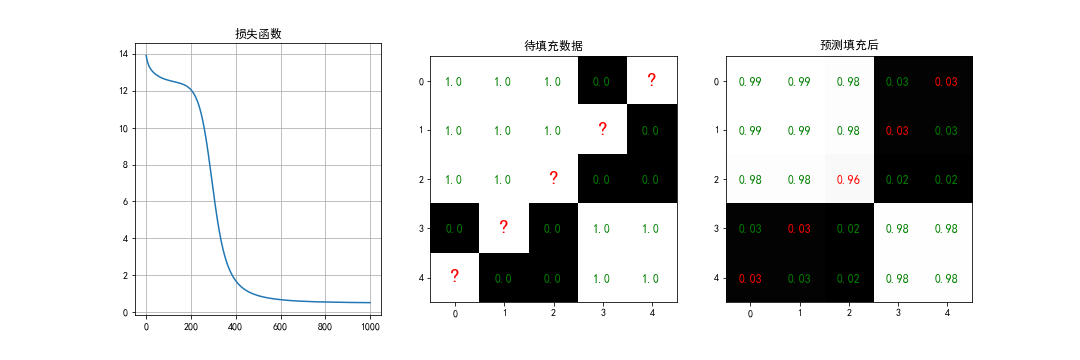
模型训练完成后，对存在缺失元素的共线矩阵$Y$进行重建/填充，实现缺失值预测。并展示结果。

# 重建填充
Y_re = np.matmul(P, Q) + p.reshape((-1, 1)) + q.reshape((1, -1)) + c
Y_re = sigmoid(Y_re)

## 结果
print_para(P, Q, p, q, c)
show_result(curve=loss, curve_name='损失函数', Y=Y, Y_re=Y_re, figname='SGD_sogmoid', save=True)
# -------------------------------------输出结果
# P = 
#  [[ 1.79  0.03]   # 用户/物品隐向量的 几何特征：
#  [ 1.79  0.16]    # 用户123 & 物品123，隐向量基本同向，线性输出o≈4，sigmoid后趋向于1；
#  [ 1.8   0.1 ]    # 用户45  & 物品45 ，隐向量基本同向，线性输出o≈4，sigmoid后趋向于1；
#  [-2.09 -0.16]    # 用户123 & 物品45 , 隐向量基本反向，线性输出o≈-4，sigmoid后趋向于0；
#  [-2.09 -0.06]]   # 用户45  & 物品123, 隐向量基本反向，线性输出o≈-4，sigmoid后趋向于0；
# Q = 
#  [[ 1.79  1.79  1.8  -2.1  -2.09]
#  [ 0.15  0.05  0.1  -0.05 -0.18]]
# p =  [ 0.49  0.49 -0.05 -0.27 -0.26]
# q =  [ 0.48  0.48 -0.06 -0.26 -0.26]
# c =  0.08

6. 梯度的几何理解

6.1 误差损失函数的梯度

（1）关于 用户/物品矩阵

无论是4.3节的

$$\begin{array}{rl}\frac{?L_e}{?P_{u,k}}& =\frac{?L_e}{?{\hat{y}}_{u,i}}\frac{?{\hat{y}}_{u,i}}{?P_{u,k}}=2({\hat{y}}_{u,i}?y_{u,i})Q_{k,i}\\ \frac{?L_e}{?Q_{k,i}}& =\frac{?L_e}{?{\hat{y}}_{u,i}}\frac{?{\hat{y}}_{u,i}}{?Q_{k,i}}=2({\hat{y}}_{u,i}?y_{u,i})P_{u,k}\end{array}$$

或者5.3节的

$$\begin{array}{rl}\frac{?L_e}{?P_{u,k}}& =\frac{?L_e}{?o_{u,i}}\frac{?o_{u,i}}{?P_{u,k}}=({\hat{y}}_{u,i}?y_{u,i})Q_{k,i}\\ \frac{?L_e}{?Q_{k,i}}& =\frac{?L_e}{?o_{u,i}}\frac{?o_{u,i}}{?Q_{k,i}}=({\hat{y}}_{u,i}?y_{u,i})P_{u,k}\end{array}$$

可以看到，损失误差$L_e$关于用户矩阵$P$或物品矩阵$Q$的梯度，都有着统一的形式，
可以把它描述为：

$$\frac{?L_e}{?\alpha }\propto \Delta y?\frac{?({\alpha }^T\beta )}{?\alpha }=\Delta y?\beta$$

其中，$\alpha ,\beta$ 代表 $P_{u,k},Q_{k,i}$（因为内积的对称性，两者顺序交换后仍然成立）。

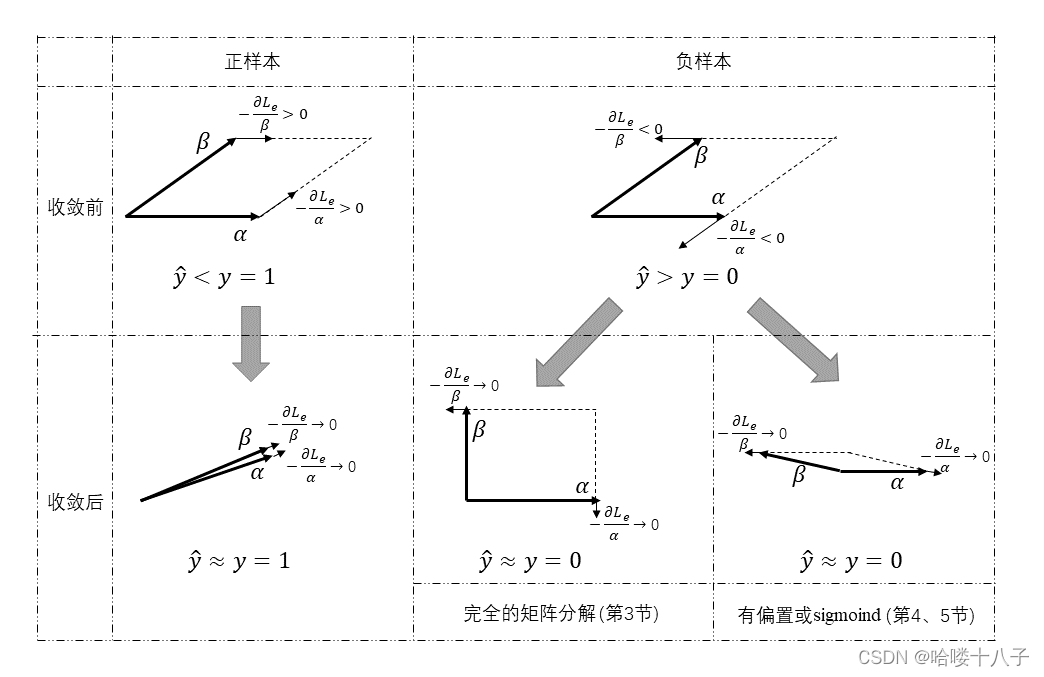
该梯度形式有两个特点：

• 梯度大小：正比于损失误差$\Delta y=\hat{y}?y$，有误差时就有梯度，误差越大梯度就越大，直到没误差之后梯度才会消失；
• 梯度方向：平行于另一个矩阵（相同的行/列的行/列向量）;

更直观的理解，如下图。

（2）关于 用户/物品/整体偏置

类比（1）中损失误差$L_e$关于用户矩阵$P$或物品矩阵$Q$梯度的分析思路，根据4.3节和5.3节对应的梯度公式，损失误差$L_e$关于用户偏置$p$/物品偏置$q$/整体偏置$c$的梯度，可以统一描述为：

$$\frac{?L_e}{?b}\propto \Delta y$$

其中，$b$ 代表 $p_u,q_i,c$三个偏置项。

该梯度形式对应的两个特点：

• 梯度大小：正比于损失误差$\Delta y=\hat{y}?y$，有误差时就有梯度，误差越大梯度就越大，直到没误差之后梯度才会消失；
• 梯度方向：标量，不存在方向。

相比（1），理解相对简单，不再赘述。

6.3 正则化损失函数的梯度

文中使用了2范数作为正则化项，其负梯度方向为参数向量的反方向。

根据4.3节中关于 正则误差$L_2$梯度 的描述。正则误差$L_2$关于任意参数（或参数向量）$\alpha$的梯度，可以统一描述为：

$$\frac{?L_2}{?\alpha }=2\alpha$$

用$\alpha$表示参数向量，用$?\frac{?L_2}{\alpha }$表示正则化损失函数对参数向量的负梯度方向，直观理解如下图。

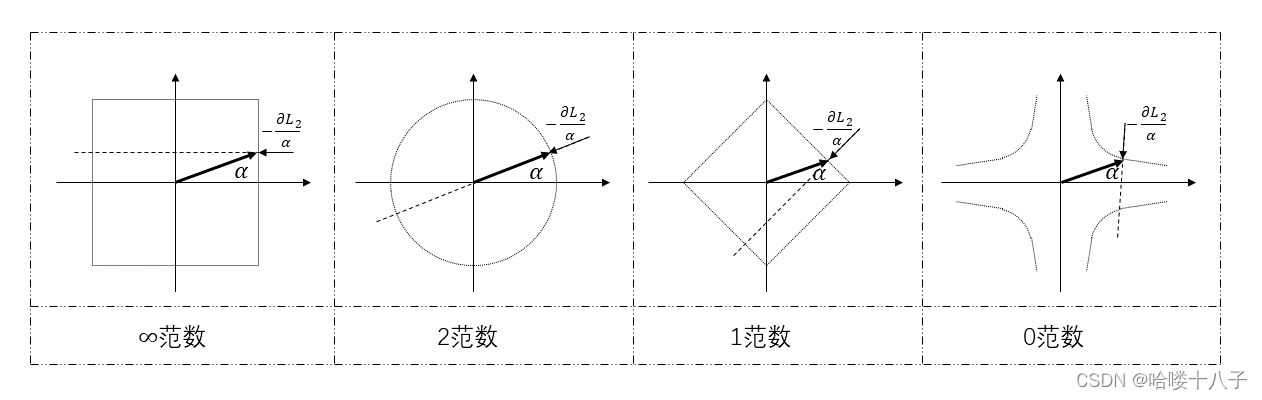
其中，关于1范数和0范数的实例，可作为p范数（$p\le 1$）有助于得到稀疏解（即参数中大多为0）的一种直观理解，即负梯度方向$?\frac{?L_2}{\alpha }$驱使参数向量$\alpha$尽可能靠近坐标轴。

PS: 另一种同样直观的几何解释相对普遍，即模型参数的最优解，为损失函数等高面 和 最小范数球的切点，对于p范数（$p\le 1$），范数球是凹的，所以切点很容易出现在范数球的“尖端”位置，也就是坐标轴上，因此参数向量在某些维度上为0。

7. Keras实现

上面几节，手动推导了梯度公式，实现了梯度下降。实际场景中，尤其对于复杂模型，一般直接使用相关计算框架，梯度下降可自动实现，不需要考虑内部细节。这里以Keras为例，实现了4、5节的 梯度下降矩阵分解。

首先，准备一个通用的模型函数，通过参数控制是否添加sigmoid层，后面直接调用。

## ================
def sigmoid_tf(x):
    return tf.exp(x) / (1 + tf.exp(x))
## ================

def build_network(sigmoid=False):
    user_id =Input([1], name='user_id')
    item_id =Input([1], name='cust_id')
    user_embd = Embedding(  input_dim=num_user, 
                            output_dim=latent,
                            name='user_embd')(user_id)
    item_embd = Embedding(  input_dim=num_item, 
                            output_dim=latent,
                            name='item_embd')(item_id)
    user_bias = Embedding(  input_dim=num_user, 
                            output_dim=1,
                            name='user_bias')(user_id)
    item_bias = Embedding(  input_dim=num_item, 
                            output_dim=1,
                            name='item_bias')(item_id)        
    output1 = Dot(2, name='inner_product')([user_embd, item_embd])
    output2 = add([output1, user_bias, item_bias])  
    output3 =Flatten()(output2)
    if sigmoid:
        output4 = Lambda(sigmoid_tf, name='sigmoid')(output3)
        model = Model( inputs=[user_id, item_id],
                      outputs=output4)
        model.compile(optimizer='adam', loss='binary_crossentropy')
    else:
        model = Model(inputs=[user_id, item_id],
                    outputs=output3)
        model.compile(optimizer='adam', loss='mse') 
    print(model.summary())
    return model

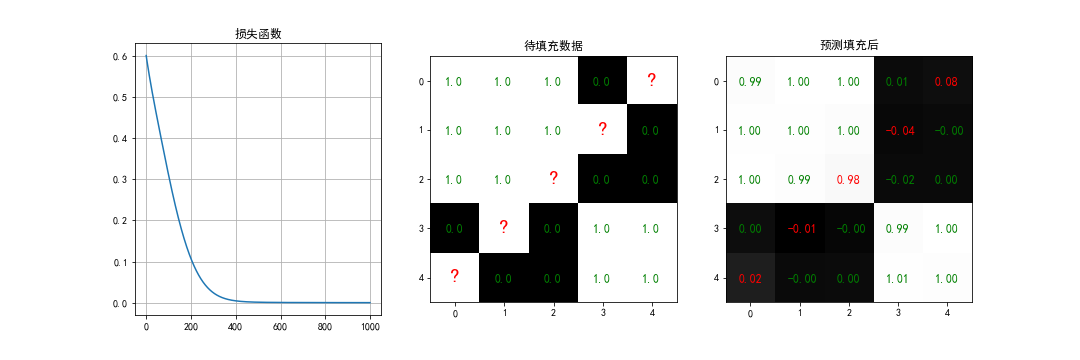
7.1 没有sigmoid(前向推理同4.1节)

# 建模
model = build_network(sigmoid=False)
# 训练
history = model.fit(  x=[dataset['user'], dataset['item']],
            y=dataset['score'],
            epochs=1000)
loss = history.history['loss']  
# 预测  
u_grid, i_grid = np.meshgrid(np.arange(num_user), np.arange(num_item))
u_grid, i_grid = u_grid.T, i_grid.T
Y_re = model.predict(x=[u_grid.reshape(-1), 
                        i_grid.reshape(-1)],
                    batch_size=8)
Y_re = Y_re.reshape((num_user, num_item))
## 结果
P, Q, p, q = model.get_weights()
print_para(P, Q, p, q)
show_result(curve=loss, curve_name='损失函数', Y=Y, Y_re=Y_re, figname='keras_linear', save=True)
# -------------------------------------输出结果
# P = 
#  [[ 0.13  0.68]
#  [ 0.2   0.69]
#  [ 0.28  0.69]
#  [ 0.19 -0.64]
#  [ 0.42 -0.59]]
# Q = 
#  [[ 0.35  0.76]
#  [ 0.22  0.8 ]
#  [ 0.13  0.77]
#  [ 0.4  -0.74]
#  [ 0.32 -0.74]]
# p =  [[0.24]
#  [0.21]
#  [0.19]
#  [0.23]
#  [0.19]]
# q =  [[0.2 ]
#  [0.19]
#  [0.22]
#  [0.21]
#  [0.24]]  
# -------------------------------------

7.2 有sigmoid(前向推理同5.1节)

# 建模
model = build_network(sigmoid=True)
# 训练
history = model.fit(  x=[dataset['user'], dataset['item']],
            y=dataset['score'],
            batch_size=16, 
            epochs=1000)
loss = history.history['loss']    
# 预测  
u_grid, i_grid = np.meshgrid(np.arange(num_user), np.arange(num_item))
u_grid, i_grid = u_grid.T, i_grid.T
Y_re = model.predict(x=[u_grid.reshape(-1), 
                        i_grid.reshape(-1)],
                    batch_size=8)
Y_re = Y_re.reshape((num_user, num_item))
## 结果
P, Q, p, q = model.get_weights()
print_para(P, Q, p, q)
show_result(curve=loss, curve_name='损失函数', Y=Y, Y_re=Y_re, figname='keras_sigmoid', save=True)   
# -------------------------------------输出结果
# P = 
#  [[-1.22 -1.24]
#  [-1.23 -1.23]
#  [-1.25 -1.23]
#  [ 1.25  1.24]
#  [ 1.17  1.16]]
# Q = 
#  [[-1.3  -1.26]
#  [-1.58 -1.65]
#  [-1.6  -1.61]
#  [ 1.74  1.68]
#  [ 1.72  1.68]]
# p =  [[ 0.47]
#  [ 0.5 ]
#  [ 0.08]
#  [-0.66]
#  [-0.14]]
# q =  [[ 0.49]
#  [-0.15]
#  [-0.38]
#  [ 0.32]
#  [ 0.33]]
# -------------------------------------