机器学习之线性回归
一、定义
线性回归是机器学习的入门知识,应用十分广泛。线性回归利用数理统计中的回归分析来确定两种或两种以上变量相互依赖的定量关系,其表达式为:y = wx + b + e(此公式采用向量表示法),误差 e 服从均值为0的正态分布。同时定义线性回归的一种损失函数 loss(损失函数一般是预测值和真实值之间的差距) 为:
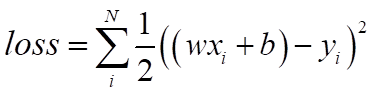
二、目的
利用随机梯度下降法(每次训练的起点真实数据(x,y)都在变化)更新参数 w 和 b 来实现最小化(min)损失函数 loss ,最终更新学得 w 和 b 的数值,使得预测数据和真实数据更加拟合。
三、原理(数学公式推导)
损失函数loss的降低取决于参数w 和 b 的数值,因此最小化(loss)的过程就是最优化方法的过程,采用随机梯度下降法,利用求导和偏导再对参数w 和 b 的数值进行梯度增减变化,最终达到最小化(min loss)。注意下面公式中的 lr 是指学习率(步长),一般由程序员自行设定可调参数大小,但设置值时一般不能太大也不能太小,太大容易无法收敛,太小梯度下降效率太低。x 和 y 表示真实值,y_p = wx + b 表示预测值。
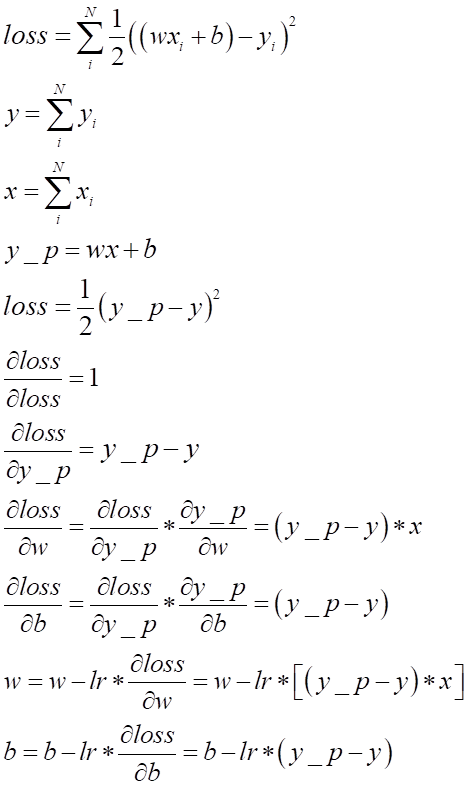
四、完整代码及部分结果
import torch as t
from matplotlib import pyplot as plt
from IPython import display
t.manual_seed(10) # 设置随机数种子,其必要性请参考博主csdn《Pytorch中设计随机数种子的必要性》此篇文章
def get_randn_data(batch_size=8):
"""产生随机数x并给线性函数y=2x+3加上噪声,便于后面学习能否拟合结果"""
x = t.randn(batch_size,1)*20
y = x * 2 + (1 + t.randn(batch_size,1))*3
return x,y # x和y都是tensor
# 随机初始化参数w和零初始化参数b,
w = t.randn(1,1)
b = t.zeros(1,1)
# 设置学习率或者步长,可更改
lr = 0.0001
# 创建列表分别存储参数w和b的变化值
listw = []
listb = []
for count in range(20000): # 训练20000次并测试输出
# 训练过程
x,y = get_randn_data() # x,y都是真实数据也就是实际值
# 前向传播,从头往后传到得出预测值,再得出损失函数下损失值
y_p = x.mm(w) + b.expand_as(y) # 实现的就是通过参数w和b和因变量x计算预测值y_p = wx + b
loss = 0.5 * (y_p - y) ** 2 # 实现的就是计算损失函数的损失值loss = 1/2(y_p - y) ** 2
loss = loss.sum() # loss为tensor格式,所以要计算损失函数的值需要全部加起来得出总和
# 非调用函数计算梯度,自行设计
# 反向传播,从后往前传通过梯度下降(求导和偏导)更新w和b,目标是min loss(减小损失值,使得预测值和真实值更加贴近匹配)
dloss = 1 # loss对loss求导
dy_p = dloss * (y_p - y) # loss对y_p求偏导
dw = x.t().mm(dy_p) # loss对w求偏导,使用转置的原因是x是[8,1],dy_p也是[8,1],相乘结果是[1,1]
# print(dy_p.size())
db = dy_p.sum() # loss对b求偏导
# inplace相减实现梯度下降,更新参数w和b
w.sub_(lr * dw)
b.sub_(lr * db)
# 测试输出过程
# 每训练1000次输出训练实现预测结果一次,画图(线和散点)
if count % 1000 == 0:
# 设置画图中横纵坐标的范围
plt.xlim(0,20)
plt.ylim(0,45)
display.clear_output(wait=True) # 清空并显示实时数据动态表示
# 训练得到的函数模型显示的线性图形
x1 = t.arange(0,20).view(-1,1) # view为-1时会tensor根据元素自动计算维度大小
x1 = x1.float()
y1 = x1.mm(w) + b.expand_as(x1)
plt.plot(x1.squeeze().numpy(),y1.squeeze().numpy())
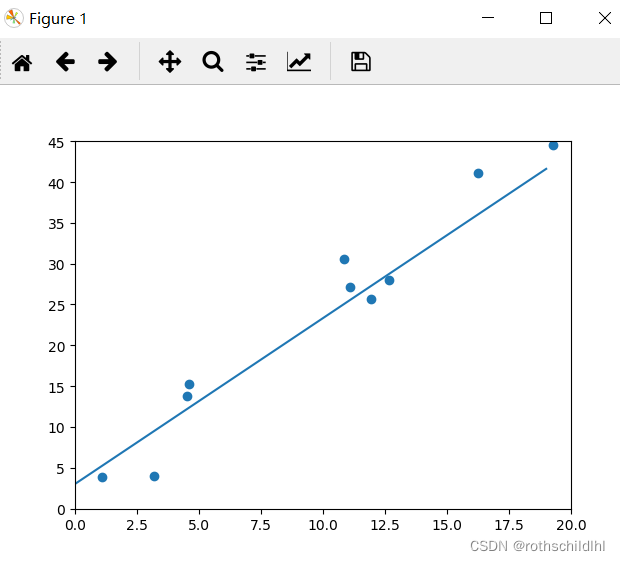
# 随机生成的测试数据,用来检验函数模型是否匹配随机测试数据点状图形
x2,y2 = get_randn_data(batch_size=20)
plt.scatter(x2.squeeze().numpy(),y2.squeeze().numpy())
# 图像输出并在2秒后自动关闭
plt.show(block=False)
plt.pause(2)
plt.close()
# 输出每次训练后的模型参数w和b的值,也可以看出w和b的变化趋势
# print(w.squeeze().numpy(), b.squeeze().numpy())
# 收集参数w和b每次训练变化的值,实现后面参数值线性回归变化点状图的显示
listw.append((w.squeeze().numpy().tolist())) # tensor->numpy->list
listb.append((b.squeeze().numpy().tolist()))
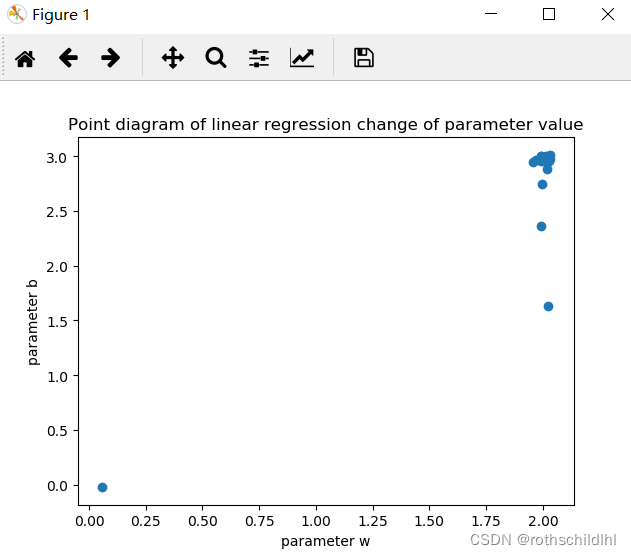
# 参数值线性回归变化点状图的显示
plt.title("Point diagram of linear regression change of parameter value")
plt.xlabel("parameter w")
plt.ylabel("parameter b")
plt.scatter(listw,listb)
plt.show(block=False)
plt.pause(30)
plt.close()
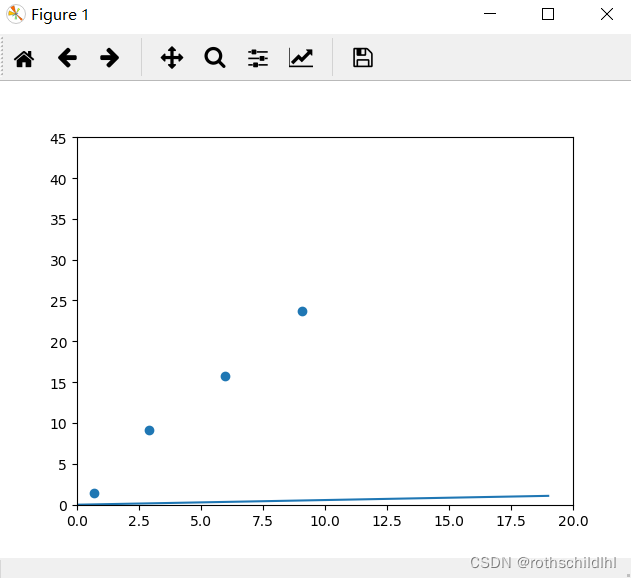
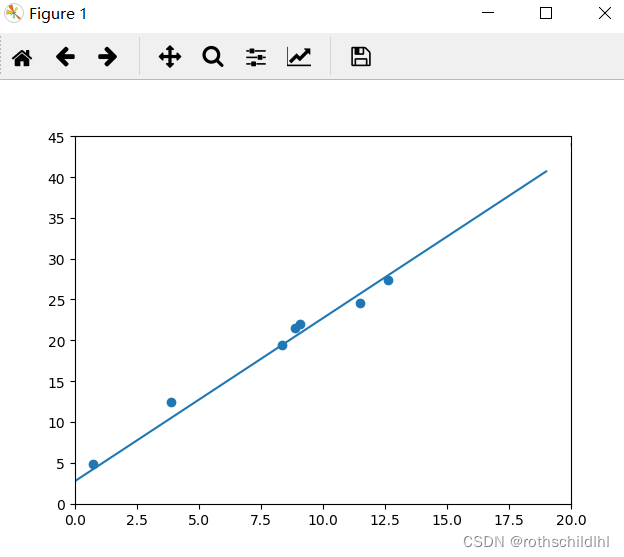

五、结果分析
通过可视化图像可以看出,训练的线性回归模型基本上已经能实现和真实测试数据的较好拟合,参数基本上也最终趋于稳定,参数 w = 2,b = 3 。