[人工智能] 第三单元用python学习微积分（二十）壳层法、圆盘法求体积 (上）

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 第三单元用python学习微积分（二十）壳层法、圆盘法求体积 (上） -> 正文阅读

[人工智能]第三单元用python学习微积分（二十）壳层法、圆盘法求体积 (上）

本文内容来自于学习麻省理工学院公开课：单变量微积分-壳层法、圆盘法求体积-网易公开课

一、切片法球体积 (继续建立积分的思想)

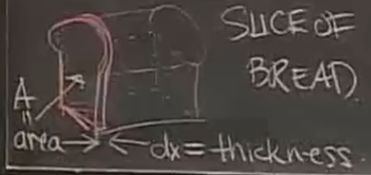
如图，红色切片部分的体积 $\Delta V = A\Delta x$

这个式子取极限，则有 $dV = A(x)dx$

全部面积为 $V = \int A(x)dx\approx \sum A_i\Delta x$

二、旋转立方体（solids of revolution)

圆盘法介绍：

老师先画了一条x轴上方曲线，看着像sinx，之后出题，这个曲线绕x轴一周形成一个椭圆，可以猜想，当对这个椭圆切片，可以得到一个?，因为图形绕x轴旋转不会改变函数值到x轴的距离，而这个距离就是这个?的半径。

于是有公式 $dV = \pi y^2dx$ ，假设这个曲线就是sin(x), 于是有体积公式 $V = \int_{0}^{\pi} \pi sin^2(x)dx$

from sympy import *
import matplotlib.pyplot as plt
import numpy as np
from enum import Enum
from itertools import product, combinations

from matplotlib import cm
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d.art3d import Poly3DCollection, Line3DCollection
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure(figsize=(12, 12),
                 facecolor='lightyellow'
                )
# draw sphere
ax = fig.gca(fc='whitesmoke',
               projection='3d' 
              )
 
class EnumAxis(Enum):
    XAxis = 1
    YAxis = 2
    ZAxis = 3
    
def fromXYZM(xyzM):
    ret = []
    
    m=range(0,xyzM.shape[0])
    
    for b in zip(m,[0]):
        ret.append((xyzM[b]))
    for b in zip(m,[1]):
        ret.append((xyzM[b]))
    for b in zip(m,[2]):
        ret.append((xyzM[b]))
    return ret

def plot_surface(x, y, z, dx, dy, dz, ax):
    xx = np.linspace(x, x+dx, 2)
    yy = np.linspace(y, y+dy, 2)
    zz = np.linspace(z, z+dz, 2)
    
    if(dz == 0):
        xx, yy = np.meshgrid(xx, yy)
        ax.plot_surface(xx, yy, z, alpha=0.25)
    
    if(dx == 0):
        yy, zz = np.meshgrid(yy, zz)
        ax.plot_surface(x, yy, zz, alpha=0.25)
    
    if(dy == 0):
        xx, zz = np.meshgrid(xx, zz)
        ax.plot_surface(xx, y, zz, alpha=0.25)
    

def plot_opaque_cube(x, y, z, dx, dy, dz, ax):

    xx = np.linspace(x, x+dx, 2)
    yy = np.linspace(y, y+dy, 2)
    zz = np.linspace(z, z+dz, 2)

    xx, yy = np.meshgrid(xx, yy)
    ax.plot_surface(xx, yy, z)
    ax.plot_surface(xx, yy, z+dz)

    yy, zz = np.meshgrid(yy, zz)
    ax.plot_surface(x, yy, zz)
    ax.plot_surface(x+dx, yy, zz)

    xx, zz = np.meshgrid(xx, zz)
    ax.plot_surface(xx, y, zz)
    ax.plot_surface(xx, y+dy, zz)
    # ax.set_xlim3d(-dx, dx*2, 20)
    # ax.set_xlim3d(-dx, dx*2, 20)
    # ax.set_xlim3d(-dx, dx*2, 20)
    
def DrawAxis(ax, xMax, yMax, zMax):
    # 设置坐标轴标题和刻度
    ax.set(xlabel='X',
           ylabel='Y',
           zlabel='Z',
           xticks=np.arange(-xMax, xMax, 1),
           yticks=np.arange(-yMax, yMax, 1),
           zticks=np.arange(-zMax, zMax, 1)
          )

    ax.plot3D(xs=[xMax,-xMax, 0,0, 0, 0, 0,0, ],    # x 轴坐标
              ys=[0, 0,0, yMax,-yMax, 0, 0,0, ],    # y 轴坐标
              zs=[0, 0,0, 0,0, 0, zMax,-zMax ],    # z 轴坐标
              zdir='z',    # 
              c='k',    # color
              marker='o',    # 标记点符号
              mfc='r',    # marker facecolor
              mec='g',    # marker edgecolor
              ms=10,    # size
            )

def Rx(x,y,z,theta):
    A = [x,y,z] * np.matrix([[ 1, 0           , 0           ],
                   [ 0, cos(theta),-sin(theta)],
                   [ 0, sin(theta), cos(theta)]])
    return fromXYZM(A)
 
def Ry(x,y,z,theta):
    A = [x,y,z] * np.matrix([[ cos(theta), 0, sin(theta)],
                   [ 0           , 1, 0           ],
                   [-sin(theta), 0, cos(theta)]])
    return fromXYZM(A)
 
def Rz(x,y,z,theta):
    A = [x,y,z] * np.matrix([[ cos(theta), -sin(theta), 0 ],
                   [ sin(theta), cos(theta) , 0 ],
                   [ 0           , 0            , 1 ]])
    return fromXYZM(A)

def XYRotateByAxis(xFrom,xTo,steps,expr,theta,color,ax,rotatedBy):
    yarr = []
    xarr = np.linspace(xFrom ,xTo, steps) 
    xyz = []
    xx = []
    yy = []
    zz = []
    for xval in xarr:
        yval = expr.subs(x,xval)
        if rotatedBy == EnumAxis.XAxis:
            xyz =  Rx(xval,yval,0,theta)
        elif rotatedBy == EnumAxis.YAxis:
            xyz =  Ry(xval,yval,0,theta)
        else:
            xyz =  Rz(xval,yval,0,theta)
            
        xx.append(xyz[0])
        yy.append(xyz[1])
        zz.append(xyz[2])
    xarr1 = []
    xarr1.append(xx)
    yarr1 = []
    yarr1.append(yy)
    zarr1 = []
    zarr1.append(zz)

    ax.plot(xx, yy, zz, color)
    
def DrawXY(xFrom,xTo,steps,expr,color,label,plt):
    yarr = []
    xarr = np.linspace(xFrom ,xTo, steps) 
    for xval in xarr:
        yval = expr.subs(x,xval)
        yarr.append(yval)
    y_nparr = np.array(yarr) 
    plt.plot(xarr, y_nparr, c=color, label=label)    

def DrawInt(xFrom,xTo,steps,expr,color,plt, label=''):
    if(xFrom < 0 and xTo < 0):
        DrawIntNegative(xFrom,xTo,steps,expr,color,plt, label)
    else:
        if(xFrom > 0 and xTo > 0):
            DrawIntPostive(xFrom,xTo,steps,expr,color,plt, label)
        else:
            DrawIntNegative(xFrom,0,steps,expr,color,plt, label)
            DrawIntPostive(0,xTo,steps,expr,color,plt, label)
    
def DrawIntNegative(xFrom1,xTo1,steps,expr,color,plt, label=''):
    xFrom = 0 - xTo1
    xTo = 0 - xFrom1
    width = (xTo - xFrom)/steps
    xarr = []
    yarr = []
    area = 0
    xprev = xFrom
    yvalAll =  0
    xarr.append(0)
    yarr.append(0)
    for step in range(steps):
        yval = expr.subs(x,xprev)
        area += width * yval
        xarr.append(0-xprev)
        yarr.append(0-area)
        xprev= xprev + width
    plt.plot(xarr, yarr, c=color, label =label)
    
def DrawIntPostive(xFrom,xTo,steps,expr,color,plt, label=''):
    width = (xTo - xFrom)/steps
    xarr = []
    yarr = []
    area = 0
    xprev = xFrom
    yvalAll =  0
    xarr.append(0)
    yarr.append(0)
    for step in range(steps):
        yval = expr.subs(x,xprev)
        area += width * yval
        xarr.append(xprev)
        yarr.append(area)
        xprev= xprev + width
    plt.plot(xarr, yarr, c=color, label =label)    
        
def DrawRects(xFrom,xTo,steps,expr,color,plt, label=''):
    width = (xTo - xFrom)/steps
    xarrRect = []
    yarrRect = []
    area = 0
    xprev = xFrom
    yvalAll =  0
    for step in range(steps):
        yval = expr.subs(x,xprev + width)
        xarrRect.append(xprev)
        xarrRect.append(xprev)
        xarrRect.append(xprev + width)
        xarrRect.append(xprev + width)
        xarrRect.append(xprev)
        yarrRect.append(0)
        yarrRect.append(yval)
        yarrRect.append(yval)
        yarrRect.append(0)
        yarrRect.append(0)
        area += width * yval
        plt.plot(xarrRect, yarrRect, c=color)    
        xprev= xprev + width
        yvalAll += yval
    print('============================')    
    if len(label)!=0:
        print(label)    
    print('============================')
    print('width = ', width)
    print('ave = ', yvalAll / steps)
    print('area = ',area)
    areaFinal = (integrate(expr, (x,xFrom,xTo)))
    print ('area final = ',areaFinal)
    print ('ave final = ', areaFinal / (xTo - xFrom))

def TangentLine(exprY,x0Val,xVal):
    diffExpr = diff(exprY)
    x1,y1,xo,yo = symbols('x1 y1 xo yo')
    expr = (y1-yo)/(x1-xo) - diffExpr.subs(x,x0Val)
    eq = expr.subs(xo,x0Val).subs(x1,xVal).subs(yo,exprY.subs(x,x0Val))
    eq1 = Eq(eq,0)
    solveY = solve(eq1)
    return xVal,solveY

def DrawTangentLine(exprY, x0Val,xVal1, xVal2, clr, txt):
    x1,y1 = TangentLine(exprY, x0Val, xVal1)
    x2,y2 = TangentLine(exprY, x0Val, xVal2)
    plt.plot([x1,x2],[y1,y2], color = clr, label=txt)
    
def Newton(expr, x0):
    ret = x0 - expr.subs(x, x0)/ expr.diff().subs(x,x0)
    return ret

DrawAxis(ax, 5,5,5)

x = symbols('x')
expr = sin(x)
DrawXY(0,np.pi,100,expr,'b','',plt)
XYRotateByAxis(0,np.pi,100,expr,-0.5*np.pi,'r',ax, EnumAxis.XAxis)
XYRotateByAxis(0,np.pi,100,expr,0.5*np.pi,'r',ax, EnumAxis.XAxis)
XYRotateByAxis(0,np.pi,100,expr,-np.pi,'b',ax, EnumAxis.XAxis)

ax.plot([2, 2],[0,sin(2)],[0,0], 'c')
ax.plot([2.1, 2.1],[0,sin(2.1)],[0,0], 'c')

expr = np.pi* sin(x)**2
ax.text(5,1,0,
           s='              min(x) = 0 \n\
              max(x) = pi \n\
              y = sin(x) \n\
              expr = np.pi* sin(x)**2 \n\
              V = integrate(expr, (x,0,np.pi)) \n\
              = '+ format(integrate(expr, (x,0,np.pi))),
           fontsize=18,
           color='darkgreen')

#print ("area  =", integrate(expr, (x,0,np.pi)))
#x = symbols('x')
#expr = sin(x)
#XYRotateByX(0,np.pi,100,expr,1*np.pi,'r',ax)
# draw sphere
#ax = fig.add_subplot(133, projection='3d')
#u, v = np.mgrid[0:2*np.pi:20j, 0:np.pi:10j]
#x = np.cos(u)*np.sin(v)
#y = np.sin(u)*np.sin(v)
#z = np.cos(v)
#ax.plot_wireframe(x, y, z, color="red")
ax.view_init(elev=20,    # 仰角
             azim=20    # 方位角
            )
plt.show()

)

?1、圆盘法(method of disk)求体积

这里老师把上方xy平面这个曲线看作是半圆，于是y的公式变作

$(x - a)^2 +y^2 = a^2$

曲线的边界变为 $x\in(0,2a)$

$y^2 = a^2 - (x - a)^2 =a^2 -(x^2-2ax+a^2) = 2ax - x^2$

考虑切片的情况，体积的计算情况不会改变

$dV = \pi y^2dx$

$V = \int_{0}^{2a} \pi( 2ax - x^2)dx =\pi(ax^2 - \frac{x^3}{3})| _{0}^{2a} = 4a^3\pi - \frac{8a^3\pi}{3} = \frac{4a^3\pi}{3}$

这里 0-2a 是球的半径，也是曲线在x轴的取值范围，当取值范围是不定值时,体积公式为

$V = \pi(ax^2 - \frac{x^3}{3})$

检查： $V = \pi(ax^2 - \frac{x^3}{3})|_{0}^{x=a} = \frac{2\pi a^3}{3}$ 确实是整圆一半的体积

fig = plt.figure(figsize=(12, 12),
                 facecolor='lightyellow'
                )
# draw sphere
ax = fig.gca(fc='whitesmoke',
               projection='3d' 
              )
x = symbols('x')
a = 2
expr = (2*a*x-x**2)**0.5
V = np.pi*(a*x**2-x**3/3).subs(x,2*a)
DrawXY(0,4,100,expr,'b','',plt)

XYRotateByAxis(0,4,100,expr,-0.5*np.pi,'r',ax, RotateAxis.XAxis)
XYRotateByAxis(0,4,100,expr,0.5*np.pi,'r',ax, RotateAxis.XAxis)
XYRotateByAxis(0,4,100,expr,-np.pi,'b',ax, RotateAxis.XAxis)


ax.text(1,-5,0,
           s='              min(x) = 0 \n\
              max(x) = 4 \n\
              y = (+\-)(2*a*x-x**2)**0.5 \n\
              V = np.pi*(a*x**2-x**3/3) \n\
              = '+ format(V),
           fontsize=18,
           color='darkgreen')

ax.view_init(elev=20,    # 仰角
             azim=20    # 方位角
            )
plt.show()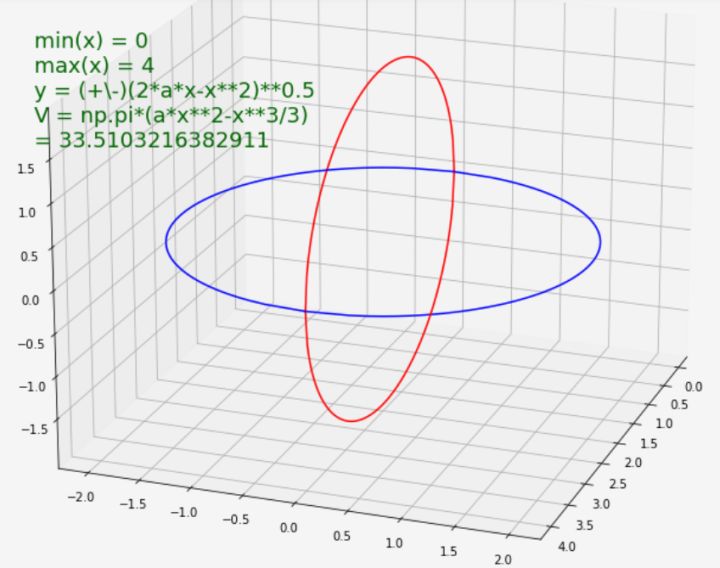