[人工智能]李航统计学习——第二章感知机（上）

第一章主要介绍了学习方法的三要素：
模型、策略、算法

这章主要介绍感知机

1 从模型来理解感知机概念

感知机是一个二分类的线性分类模型。

无论是机器学习还是深度学习，按着三要素走（模型->策略->算法）
模型本质还是假设空间(Hypothesis Space)：所有可能的条件概率分布或决策函数。而假设空间（模型）是由参数空间决定的。

【补】
假设空间是所有可能决策函数的集合；
而每个决策函数由一个参数向量决定；
参数空间：所有可能的参数向量组成的空间

举个例子：线性$y=w^{T}x+b$ 这里是由所有的$w,b$ 构成集合决定的假设空间。
因此，


感知机：从输入空间到输出空间的函数，这个函数就称作感知机。

从几何角度来理解感知器

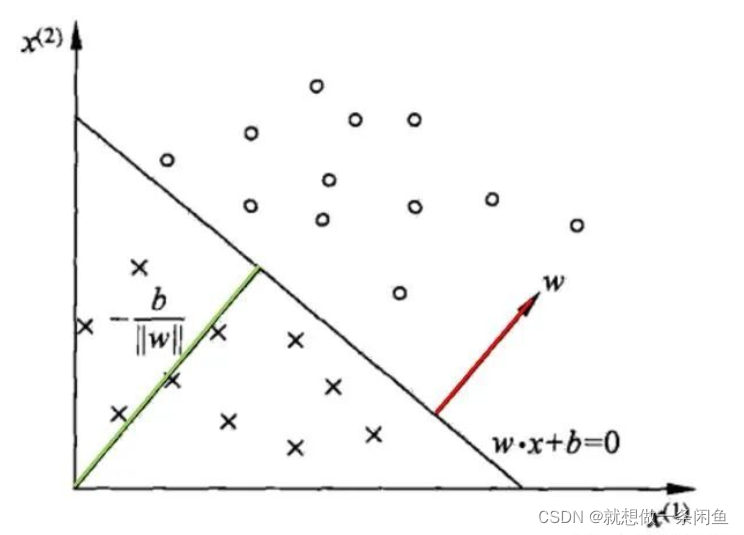
先科普超平面S：在几何中，如果环境空间是n维的，那么它所对应的超平面其实就是一个n-1 维的子空间。换句话说，超平面是比他所处的环境空间小一个维度的子空间。
举个例子来说明，如果是一个二维平面，那么超平面就是直线；如果是一维平面，超平面则就是实点，以此类推。

为什么需要超平面S？
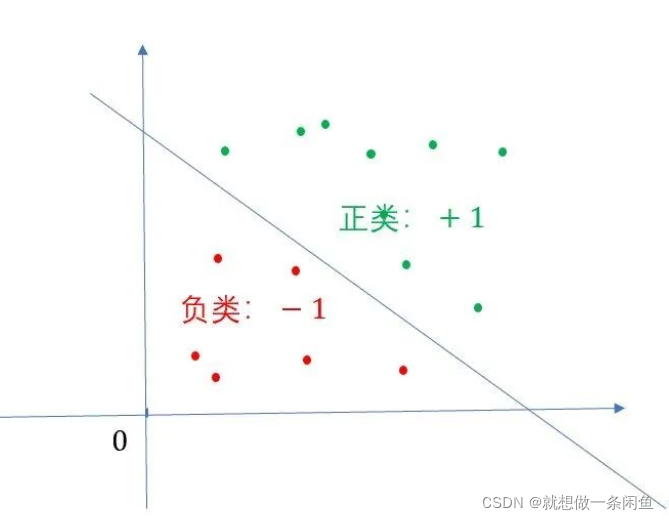
个人的理解是因为感知器是一个二分类的线性模型，输出空间是一个只包含+1和-1的一个集合，+1是正类，-1是负类; 需要区分正负类，而区分这个正负类就是超平面S的存在。

红色线，是法向量；绿色这条线，代表的是原点到超平面的距离，我们需要使其距离和最短。

2 学习策略

感知机模型，必要条件是要求数据集必须是线性可分的。
线性可分：对于给定的数据集，如果存在某个超平面，使得这个数据集的所有实例点可以完全划分到超平面的两侧，也就是正类和负类。我们就称这个数据集是线性可分的，否则线性不可分。

策略则需要合理地定义感知机相应的损失函数，如经验风险最小化策略或结构风险最小化策略。
最小化损失函数就是我们学习的策略：

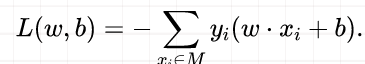
3 算法

感知机的算法有两种形式：原始形式和对偶形式。

3.1 原始形式

如何求参数w和b，通过寻找使损失函数最小的参数。