各位读者小伙伴们,大家好,时隔三个月,你们的小曾哥又回来了,今天主要跟大家分享一篇主动学习领域的文章。
Boosting Active Learning via Improving Test Performance
通过提高测试性能来促进主动学习
下载地址:https://arxiv.org/pdf/2112.05683.pdf
该篇文章是由王天阳,1李行健等学者发表在AAAI2022会议上
文章目录
摘要 Abstract
小曾哥提示:摘要是一篇文章的精髓,短小精悍,用简洁的语言来概括出整篇文章的动机以及亮点。
目标:主动学习 (AL) 的核心是应该选择哪些数据进行注释。
传统方法:试图选择高度不确定或信息丰富的数据进行注释。
问题: 不清楚所选数据如何影响 AL 中使用的任务模型的测试性能。
本文贡献:
- 在这项工作中,我们通过理论上证明选择更高梯度范数的未标记数据会导致测试损失的上限更低,从而产生更好的测试性能来探索这种影响。
- 为了应对缺乏标签信息的挑战,我们提出了两种方案,即expected-gradnorm 和entropy-gradnorm。前者通过构建预期的经验损失来计算梯度范数,而后者则通过熵构建无监督损失。
- 将这两种方案整合到一个通用的 AL 框架中。
- 在经典图像分类和语义分割任务上评估我们的方法, 结果表明,我们的方法相对于现有技术实现了卓越的性能。
介绍 introduction
小曾哥提示:主动学习的提出目标就是”降本提效“,降低标注成本,通过选择少量的样本进行标注以提升模型的最佳效果。
主动学习背景:在大多数情况下,监督学习仍然是训练深度神经网络最可靠的方式。 然而,数据注释通常可以说是昂贵的。 为了降低成本,可以使用主动学习(AL)来选择所有未标记数据的一部分进行注释,然后使用注释数据以监督方式训练任务模型(例如 CNN)。
目标:是在给定特定注释预算的情况下获得任务模型的最佳测试性能。
主动学习问题定义:应该选择哪些数据进行标注才能达到这个目标?
传统的两类主动学习方法:1、基于不确定性:旨在选择最不确定的数据进行注释 ;2、基于多样性:旨在选择可以使标记池多样化的未标记数据;
现有方法存在的问题:很少有工作探索所选数据与 AL 中使用的任务模型的测试性能之间的联系【换而言之:如果选择一个未标记的样本进行标注并用于训练任务模型,那么模型的测试性能将如何受到影响】, 这种联系可以指导我们选择有助于提高测试性能的未标记数据。
小曾哥提示:在这里通常是现有方法存在的问题,也是一篇文章的主要动机(Motivation),通过解决现有方法提出的问题,进一步突出本文的贡献。
本文贡献:
- 我们从根本上制定了主动学习中的测试性能,发现其主要影响因素是梯度范数,可以有效指导未标记数据的选择。
- 我们提出了两种方案来计算未标记数据的梯度范数,而无需求助于真实标签。
- 我们证明了所提出的方法在经典计算机视觉挑战以及计算生物学领域任务中取得了卓越的性能。
相关工作 Related work


方法 Methodology
主要内容概括:
1、利用影响函数来分析如果选择单个样本进行注释并用于训练,测试性能会受到怎样的影响,结论表明选择和注释更高梯度范数的未标记数据将导致测试损失的上限更低,从而获得更好的测试性能,这是第一个从理论上分析数据选择如何影响 AL 测试性能的工作。
2、我们提出了两种独立的方案来计算梯度范数,因为由于 AL 设置中缺乏标签信息,因此在数据选择过程中无法直接获得梯度范数。在第一个方案(即预期梯度范数)中,受的启发,我们利用所有可能的标签来计算预期的经验损失,该损失用于计算梯度范数.在第二种方案中,我们使用熵作为损失来计算梯度范数,而不使用任何标签信息。还解释了这两种方案的基本原理。
3、我们提出了一个通用的 AL 框架来整合这两种方案。
1、选择什么数据
评估 AL 方法的主要标准是任务模型的测试性能, 我们的最终目标是选择未标记的数据,使任务模型产生更好的测试性能。
根据 (Koh and Liang 2017),我们知道给定模型 fθ,例如神经网络,从其训练集中移除样本 x 将大致影响测试样本 xj 的损失:
I
l
o
s
s
(
x
,
x
j
)
=
1
n
?
θ
L
(
f
θ
(
x
j
)
)
?
H
θ
?
1
?
θ
L
(
f
θ
(
x
)
)
I_{l o s s}\left(x, x_{j}\right)=\frac{1}{n} \nabla_{\theta} L\left(f_{\theta}\left(x_{j}\right)\right)^{\top} H_{\theta}^{-1} \nabla_{\theta} L\left(f_{\theta}(x)\right)
Iloss?(x,xj?)=n1??θ?L(fθ?(xj?))?Hθ?1??θ?L(fθ?(x))
其中 n 表示现有训练样本的数量,fθ(·) 是指产生模型 fθ 的 logits正向输出步骤,并且 Hθ 是所有训练样本的平均 Hessian(Hessian矩阵并且假定是正定矩阵,代表函数的局部曲率)。 对于每个训练样本,由于我们想计算它对测试数据集中所有样本的影响(如果被移除),我们计算总影响如下
∑
j
I
loss?
(
x
,
x
j
)
=
1
n
∑
j
?
θ
L
(
T
c
+
1
(
x
j
)
)
?
H
θ
?
1
?
θ
L
(
T
c
+
1
(
x
)
)
\sum_{j} I_{\text {loss }}\left(x, x_{j}\right)=\frac{1}{n} \sum_{j} \nabla_{\theta} L\left(T^{c+1}\left(x_{j}\right)\right)^{\top} H_{\theta}^{-1} \nabla_{\theta} L\left(T^{c+1}(x)\right)
j∑?Iloss??(x,xj?)=n1?j∑??θ?L(Tc+1(xj?))?Hθ?1??θ?L(Tc+1(x))
其中Tc + 1代替1式中的 fθ,作为任务模型;同时计算的是去除X样本后,对所有测试样本的总影响。
如 (Koh and Liang 2017) 所示,虽然当训练样本对个体 xj 有害时 Iloss(x, xj) 可能为负值,但 Iloss(x, xj) 通常为正值。 直观地说,这意味着删除训练样本会增加预期的测试损失。
在 AL 设置中,假设 Tc+1 的测试损失为 Lc+1 测试,如果一个训练样本 x 从标记池中移除并且不参与训练 Tc+1,那么受影响的测试损失 Lc+1 测试可以 计算为
L test? ′ c + 1 = L test? c + 1 + ∑ j I loss? ( x , x j ) = L test? c + 1 + 1 n ∑ j ? θ L ( T c + 1 ( x j ) ) ? H θ ? 1 ? θ L ( T c + 1 ( x ) ) \begin{aligned} L_{\text {test }}^{\prime c+1} &=L_{\text {test }}^{c+1}+\sum_{j} I_{\text {loss }}\left(x, x_{j}\right) \\ &=L_{\text {test }}^{c+1}+\frac{1}{n} \sum_{j} \nabla_{\theta} L\left(T^{c+1}\left(x_{j}\right)\right)^{\top} H_{\theta}^{-1} \nabla_{\theta} L\left(T^{c+1}(x)\right) \end{aligned} Ltest?′c+1??=Ltest?c+1?+j∑?Iloss??(x,xj?)=Ltest?c+1?+n1?j∑??θ?L(Tc+1(xj?))?Hθ?1??θ?L(Tc+1(x))?
最终获得的化简近似公式为:
L
test?
c
+
1
≤
L
test?
c
+
1
+
1
n
∥
?
θ
L
(
T
c
+
1
(
x
)
)
∥
?
∥
∑
j
H
θ
?
1
?
θ
L
(
T
c
+
1
(
x
j
)
)
∥
?
L
test?
c
+
1
+
1
n
∥
?
θ
L
(
T
c
(
x
)
)
∥
?
∥
∑
i
H
θ
?
1
?
θ
L
(
T
c
+
1
(
x
j
)
)
∥
\begin{aligned} L_{\text {test }}^{c+1} & \leq L_{\text {test }}^{c+1}+\frac{1}{n}\left\|\nabla_{\theta} L\left(T^{c+1}(x)\right)\right\| \cdot\left\|\sum_{j} H_{\theta}^{-1} \nabla_{\theta} L\left(T^{c+1}\left(x_{j}\right)\right)\right\| \\ & \lesssim L_{\text {test }}^{c+1}+\frac{1}{n}\left\|\nabla_{\theta} L\left(T^{c}(x)\right)\right\| \cdot\left\|\sum_{i} H_{\theta}^{-1} \nabla_{\theta} L\left(T^{c+1}\left(x_{j}\right)\right)\right\| \end{aligned}
Ltest?c+1??≤Ltest?c+1?+n1?∥∥??θ?L(Tc+1(x))∥∥??∥∥∥∥∥?j∑?Hθ?1??θ?L(Tc+1(xj?))∥∥∥∥∥??Ltest?c+1?+n1?∥?θ?L(Tc(x))∥?∥∥∥∥∥?i∑?Hθ?1??θ?L(Tc+1(xj?))∥∥∥∥∥??
表示在周期c+1中,移除一个||?θL(Tc(x))||的训练样本x 将导致更高的 Lc+1 测试上限。 因此,这样的 x 应该保留在周期 c + 1 的标记训练池中。相反,从周期 c 的角度来看,在数据选择过程中,||?θL(Tc(x))|| 的未标记样本越多,||?θL(Tc(x))|| 应选择注释并添加到标记池中以训练 Tc+1。 这样的数据选择方案有助于 Tc+1 保持 Lc+1 测试的下界。
因此,我们得出结论,在 AL 中应该选择具有更高梯度范数的未标记数据进行标注。

小曾哥提示:大家如果觉得都是公式,不太好理解,其实可以看一下上面这张图,有助于帮助理解,思路清晰,大家如果觉得清晰,请在评论区评论一波清晰。
2、计算梯度范数
目的:选择导致更高 ||?θL(Tc(x))|| 的未标记数据 x,以降低测试损失的上限
存在的问题:缺乏 x 的标签信息,计算经验损失 L 是不可行的。
解决方案:提出了两种计算||?θL(Tc(x))||的方案,分别是预期梯度范数(expected grad norm)和 熵梯度方案(entropy-grad norm)。
预期梯度范数 Expected-Gradnorm Scheme
为了计算 | | |Θl (Tc(x))||, 我们需要先计算损失L,但是L不能直接计算未标记数据,因此我们建议使用预期经验损失来近似实际经验损失。假设给定的未标记池中有N个类,我们使用yi表示第i个类的标签。
L
e
x
p
(
T
c
(
x
)
)
=
∑
i
=
1
N
P
(
y
i
∣
x
)
L
i
(
T
c
(
x
)
,
y
i
)
L_{e x p}\left(T^{c}(x)\right)=\sum_{i=1}^{N} P\left(y_{i} \mid x\right) L_{i}\left(T^{c}(x), y_{i}\right)
Lexp?(Tc(x))=i=1∑N?P(yi?∣x)Li?(Tc(x),yi?)
其中 P(yi|x) 是在 Tc(x) 上使用 softmax 获得的后验,Li 是当第 i 个候选标签被假设为 x 的真实标签时的经验损失。
该方案可以很容易地用于分类问题
熵梯度方案
在这个方案中,我们使用输出熵来计算梯度范数。 具体来说,我们使用网络的 softmax 输出的可微熵作为损失函数,每个样本x的熵损耗定义为:
L
e
n
t
(
T
c
(
x
)
)
=
?
∑
i
=
1
N
P
(
y
i
∣
x
)
log
?
P
(
y
i
∣
x
)
L_{e n t}\left(T^{c}(x)\right)=-\sum_{i=1}^{N} P\left(y_{i} \mid x\right) \log P\left(y_{i} \mid x\right)
Lent?(Tc(x))=?i=1∑N?P(yi?∣x)logP(yi?∣x)
选择熵的合理性:
- 根据方程式。如图 5 所示,添加更高梯度范数的训练样本预计会降低测试样本的熵。在分类问题中,降低熵通常有利于降低典型的监督损失,例如交叉熵。
- 当任务模型训练有素时(一个好的模型,例如在后来的 AL 循环中),熵很好地近似于交叉熵(Srinivas 和 Fleuret 2018)。
3、提出主动学习框架
为了利用我们的理论发现,我们开发了一个通用的 AL 框架来整合上一节中介绍的两种方案。
如下图可知,就是传统的主动学习的框架进行细微的修改,只是将任务进行分类,使其易于针对不同的场景实施。

实验 Experiment
图像分类
分类数据集: Cifar10 (2009), Cifar100 (2009), SVHN (2011), Caltech101 (2006)和 ImageNet(2009)
模型选择:ResNet-18
基线: 随机选择、core-GCN(2021)、sraal(2020)、vaal( 2019)、ll4al (2019)、core-set (2018)、QBC ( 2018) 和 mc-dropout (2016)
对比方法:exp-gn (expected-gradnorm) 和 entgn (entropy-gradnorm)
结果分析:

我们的方法在所有数据集上都优于基线,对于每个注释预算,我们的方法比其他方法产生更高的准确性。
语义分割
该实验证明了所提出方法与任务无关的性质。
数据集: Cityscapes (2016) ,是大规模的,由来自 50 个城市的街景视频序列组成
模型选择:扩张残差网络(DRN-D-22)
基线: 随机选择、core-GCN(2021)、sraal(2020)、vaal( 2019)、ll4al (2019)、core-set (2018)、QBC ( 2018) 和 mc-dropout (2016)
对比方法:exp-gn (expected-gradnorm) 和 entgn (entropy-gradnorm)

使用 mIoU(mean Intersection-over-Union)来衡量每种方法的性能。对于所有注释预算,我们的方法始终比其他方法产生更好的结果。 此外,由于我们的方法不依赖于高级学习方式(例如对抗性学习),因此无需根据任务更改定制训练方案,从而使我们的方法与任务无关。
倾向于选择更高梯度范数的更多数据

通过较高梯度范数的选定样本数(K = 2500)比较 AL 方法,可以根据上图中看出,预期梯度范数和熵范数的方法在注释前budget的百分比中,所占较高梯度范数的样本数量最多,有显著优势。
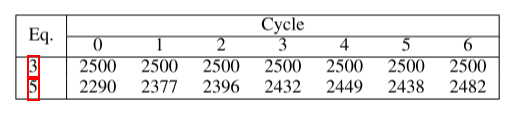
方程式中边界的定量评估
在上面推导公式阶段,公式5是在公式3的基础上取的近似,这个实验就证明公式5的效果跟公式3对比效果,如下表所示,超过 90% 的所选样本在原始(方程 3)和近似标准(方程 5)之间是一致的。
更好的泛化
在这里,我们比较了在不同 AL 方法选择的数据上训练的任务模型的泛化。 具体来说,在每个 AL 循环之后,我们计算训练和测试准确度之间的差距。 这个值越小越好,因为越大表明任务模型越容易受到过度拟合的影响。 如表 3 所示,我们的方法产生的差距最小,证明了其优越的泛化能力。

结论
在本文中,我们从理论上分析了数据选择与主动学习中使用的任务模型的测试性能之间的联系。 我们证明了选择具有更高梯度范数的未标记数据可以降低测试损失的上限。 我们提出了两个独立的方案来计算梯度范数和一个通用的主动学习框架来利用这些方案。 我们对各种基准数据集进行了广泛的实验,有希望的结果验证了我们的理论发现和提出的方案。