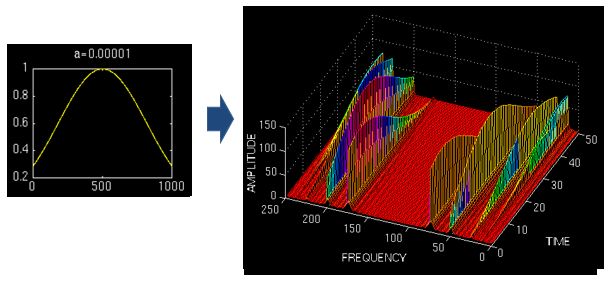
一、傅里叶变换
1、傅里叶变换基础
参考:深入浅出的讲解傅里叶变换
傅里叶变换:一段信号可以由若干频率不同的正弦信号叠加构成,DFT将将信号从时域变换到频域
用途:
滤波:从一个时域图里剔除组成它的某个频域成分很不容易;但是从频域图里剔除这个成分很容易- 求
解微分方程 故障诊断:健康的设备的时域曲线图是相似的,异常设备的是不同的,但这一点在时域图种不易被发现,转换到频域图中容易发现异常。也可以用于心电图异常检测。电能质量分析:谐波分析
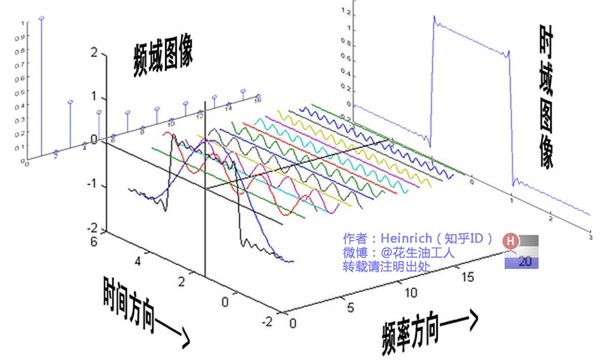
2、傅里叶变换形式规律
-
离散<---------->周期
-
连续<---------->非周期
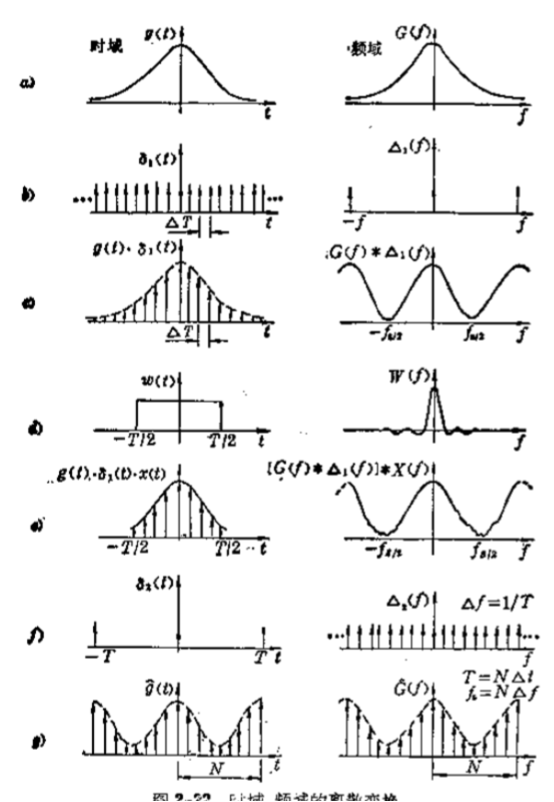
3、一些关键概念
1、离散傅里叶变换(DFT)
离散傅里叶变换(discrete Fourier transform) 傅里叶分析方法是信号分析的最基本方法,傅里叶变换是傅里叶分析的核心,通过它把信号从时间域变换到频率域,进而研究信号的频谱结构和变化规律。但是它的致命缺点是:计算量太大,时间复杂度太高,当采样点数太高的时候,计算缓慢,由此出现了DFT的快速实现,即下面的快速傅里叶变换FFT。
2、快速傅里叶变换(FFT)
计算量更小的离散傅里叶的一种实现方法。详细细节这里不做描述。
3、采样频率以及采样定理
采样频率:采样频率,也称为采样速度或者采样率,定义了每秒从连续信号中提取并组成离散信号的采样个数,它用赫兹(Hz)来表示。采样频率的倒数是采样周期或者叫作采样时间,它是采样之间的时间间隔。通俗的讲采样频率是指计算机每秒钟采集多少个信号样本。
采样定理:所谓采样定理 ,又称香农采样定理,奈奎斯特采样定理,是信息论,特别是通讯与信号处理学科中的一个重要基本结论。采样定理指出,如果信号是带限的,并且采样频率高于信号带宽的两倍,那么,原来的连续信号可以从采样样本中完全重建出来。
定理的具体表述为:在进行模拟/数字信号的转换过程中,当采样频率fs大于信号中最高频率fmax的2倍时,即
f s > 2 ? f m a x fs>2*fmax fs>2?fmax
采样之后的数字信号完整地保留了原始信号中的信息,一般实际应用中保证采样频率为信号最高频率的2.56~4倍;采样定理又称奈奎斯特定理。
4、如何理解采样定理?
在对连续信号进行离散化的过程中,难免会损失很多信息,就拿一个简单地正弦波而言,如果我1秒内就选择一个点,很显然,损失的信号太多了,光着一个点我根本不知道这个正弦信号到底是什么样子的,自然也没有办法根据这一个采样点进行正弦波的还原,很明显,我采样的点越密集,那越接近原来的正弦波原始的样子,自然损失的信息越少,越方便还原正弦波。故而
采样定理说明采样频率与信号频率之间的关系,是连续信号离散化的基本依据。 它为采样率建立了一个足够的条件,该采样率允许离散采样序列从有限带宽的连续时间信号中捕获所有信息。
3、python 实现傅里叶变换
import matplotlib.pyplot as plt
import numpy as np
import numpy.fft as fft
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示符号
Fs = 250 # 采样频率 按香农采样定理,采样频率为最高频率的2倍即可
T = 1 / Fs # 采样周期
L = 1000 # 信号长度
t = [i * T for i in range(L)]
t = np.array(t)
S = 0.4 + 0.7 * np.cos(2 * np.pi * 50 * t + 20 / 180 * np.pi) + 0.2 * np.cos(
2 * np.pi * 100 * t + 70 / 180 * np.pi) # 最高频率100
complex_array = fft.fft(S) # 快速傅里叶变换,返回结果为1000个复数,复数的模为幅值;复数的角度为相频
complex_real = complex_array.real # 获取实数部分
complex_imag = complex_array.imag # 获取虚数部分
print(complex_array.shape) # (1000,)
print(complex_array.dtype) # complex128
print(complex_array[1]) # (-2.360174309695419e-14+2.3825789764340993e-13j)
#################################
plt.subplot(311)
plt.grid(linestyle=':')
plt.plot(1000 * t[1:51], S[1:51], label='S') # 原始序列
plt.xlabel("t(毫秒)")
plt.ylabel("S(t)幅值")
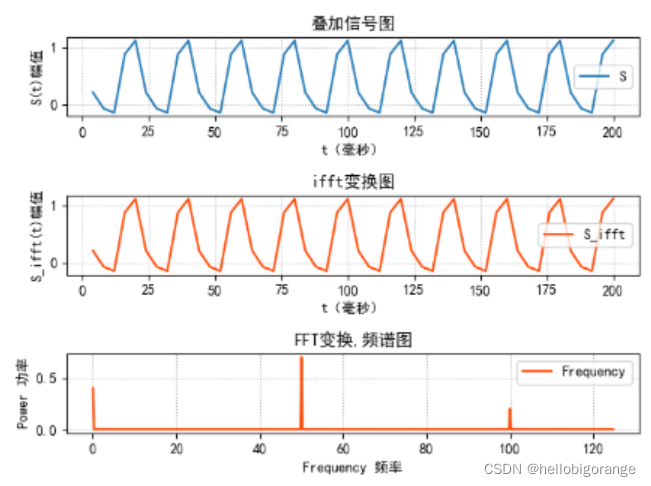
plt.title("叠加信号图")
plt.legend()
###################################
# 傅里叶逆变换
plt.subplot(312)
S_ifft = fft.ifft(complex_array)
# S_new是ifft变换后的序列
plt.plot(1000 * t[1:51], S_ifft[1:51], label='S_ifft', color='orangered')
plt.xlabel("t(毫秒)")
plt.ylabel("S_ifft(t)幅值")
plt.title("ifft变换图")
plt.grid(linestyle=':')
plt.legend()
###################################
# 得到分解波的频率序列
freqs = fft.fftfreq(t.size, t[1] - t[0]) # 从0开始,既有正的频率,又有负的,只取一半即可
# 复数的模为信号的振幅(能量大小)
pows = np.abs(complex_array) / (Fs * 2)
pows[freqs == 0] = pows[freqs == 0] / 2 # 频率为0的重复累积了两次,需要减半处理
pows = pows[freqs >= 0] # 取出对应的正频率的幅值
freqs = freqs[freqs >= 0]
plt.subplot(313)
plt.title('FFT变换,频谱图')
plt.xlabel('Frequency 频率')
plt.ylabel('Power 功率')
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
plt.plot(freqs[freqs >= 0], pows[freqs >= 0], c='orangered', label='Frequency')
plt.legend()
plt.tight_layout()
plt.show()
二、短时傅里叶变换(STFT)
https://www.zhihu.com/question/22864189/answer/40772083
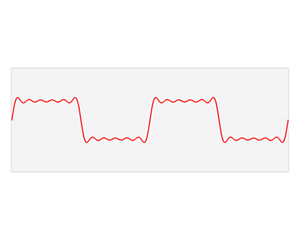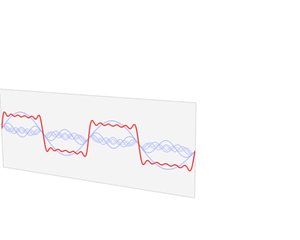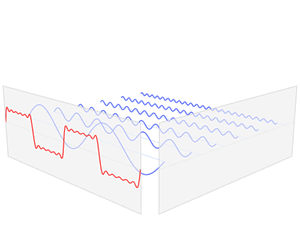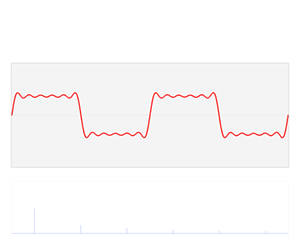
提出原因:由于FFT对于处理不平稳序列具有天然的缺陷、只能看由多少频率组成,并不能看频率出现的时间(由下图可以观察到,最上面的图为平稳系列,下面两个图为平稳的时间序列、但他们的频域图完全相同)。
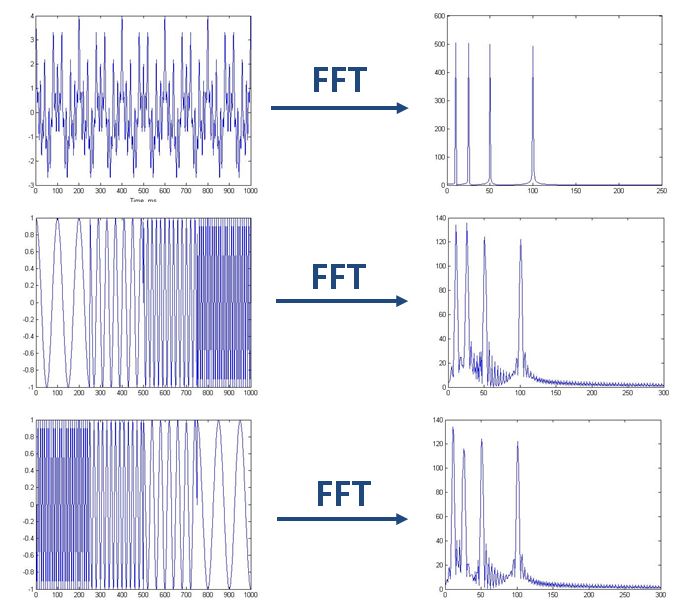
对待上述缺陷,一个可行的方式就是加窗:把整个时域过程分解成无数个等长的小过程,每个小过程近似平稳,再傅里叶变换,就知道在哪个时间点上出现了什么频率了。”这就是短时傅里叶变换。
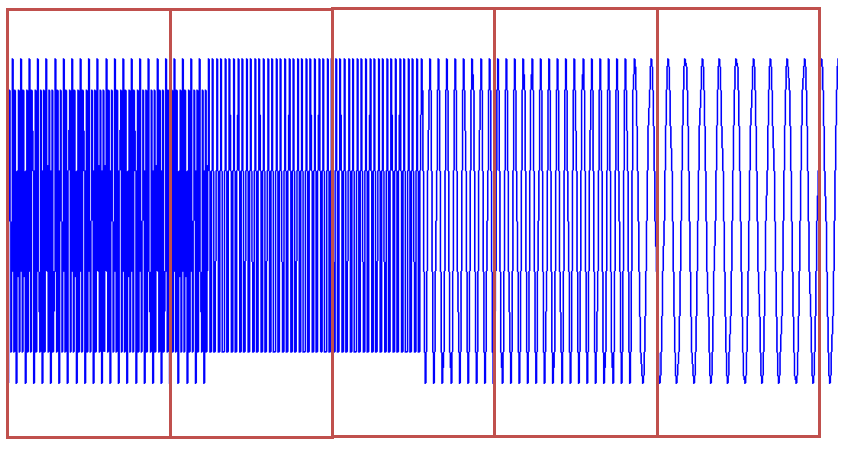
==STFT:==给时域信号加窗,再对每个窗口的时域信号做FFT变换(分段FFT),这样就可以得到频域信号的时间信息了。
缺陷,窗的大小不好控制,太窄,频域信息不易提取;太宽,时域信息模糊