1、径向畸变
????????径向畸变:图像像素以即便点中心为中心点,沿着径向产生的位置偏差,从而导致图像中所形成的像发生形变。
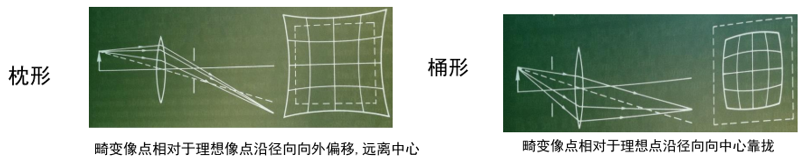
2、径向畸变建模
????????图像放大率随距光轴距离的增加而减小。在投影矩阵前加上个畸变模型大小为3*3的Slamda,相当于在坐标映射前加了x-y方向的放缩系数。
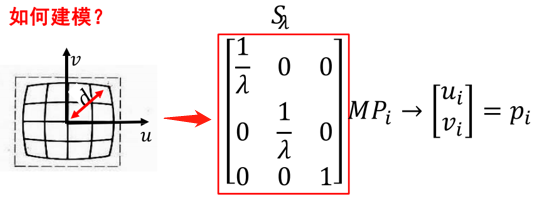
????????lamda通过一个与中心点距离相关的多项式拟合。
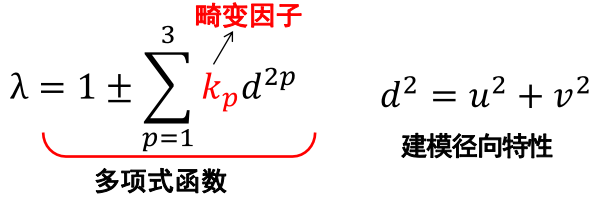
????????将畸变的投影矩阵定义为Q,得到Q矩阵的映射关系:
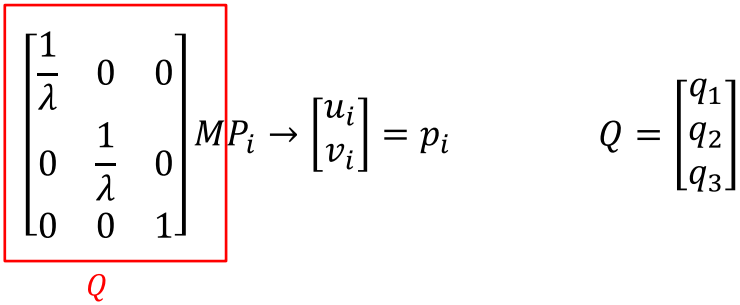
????????像素与三维世界坐标系下坐标的关系变为:

????????整理得,Q矩阵中存在畸变参数是个未知的变量,所以表达式不是线性变换:

????????给定 n 对点对应,最终问题:

????????最小二乘解:

牛顿法与列文伯格-马夸尔特法(L-M方法)
????????1)从初始解开始迭代,若初始解与实际相距较远,可能会很慢(求解系统的线性部分以找到近似解,使用该解作为整个系统的初始条件);
????????2)估计解可能是初始解的函数(由于局部最小值);
????????3)牛顿法需计算一阶段到矩阵J(雅克比矩阵),二阶导矩阵H(海塞矩阵);
????????4)L-M算法不用计算H。
????????实际中使用时,有现成的包可以调用,不用担心计算过程。
求解线性部分:
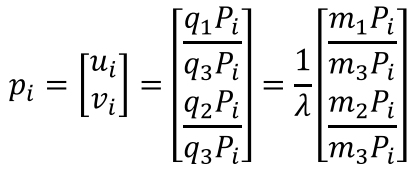
????????上面的式子,使用ui/vi可以消掉lamda这个非线性的因素:
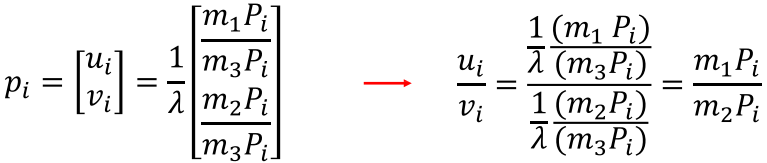
????????写成线性方程组:

????????一旦估计出 m1 和 m2,m3,k1,k2,k3 是关于 m1,m2 的非线性函数。使用牛顿法与列文伯格-马夸尔特法(L-M方法)。14个参数有8个已知了,收敛会更快。