本文根据自己对分类模型的评价指标的理解以及其它博主的理解进行总结而成,有疑问或不对地方,请留言指出。
1. 什么是评价指标?
评价指标:是针对 同份数据,不同算法模型 或者 同模型但不同模型参数,而给出这个算法或者参数好坏的定量指标;
常用的评价指标(分类模型):准确率(Accuracy)、精确率(Precision)、召回率(Recall)、P-R曲线(Precision-Recall Curve)、F1 Score、混淆矩阵(Confuse Matrix)、ROC、AUC。
为什么要有这么多度量指标呢?
这是由我们的分类任务的性质所决定的,比如在商品推荐系统中,希望更精准的了解客户需求,避免推送用户不感兴趣的内容,精确率(Precision)查准率就更加重要;在疾病检测的时候,我们不希望查漏任何一项疾病,这时查全率就更重要。当两者都需要考虑时,F1度量就是一种参考指标。
注意:评价模型过程中,需要不同的评价指标从不同角度对模型进行全面的评价,在诸多的评价指标中,大部分指标只能片面的反应模型的一部分性能,如果不能合理的运用评估指标,不仅不能发现模型本身的问题,而且会得出错误的结论。
2. 分类模型的评价指标
2.1 混淆矩阵(Confuse Matrix)
评价指标虽多,但是万变不离其宗,所有的指标其实都是衍生自混淆矩阵中。
**混淆矩阵(Confusion Matrix),可以使人们更好地了解分类中的错误。**如果矩阵中的非对角元素均为0,就会得到一个完美的分类器。下图的混淆矩阵只针对二分类问题得到的。

真正例(True Positive,TP):一个正例被正确预测为正例
真反例(True Negative,TN):一个反例被正确预测为反例
假正例(False Positive,FP):一个反例被错误预测为正例
假反例(False Negative,FN):一个正例被错误预测为反例
2.2 准确率(Accuracy)
准确率是所有样本中预测正确的样本占比,其公式如下:
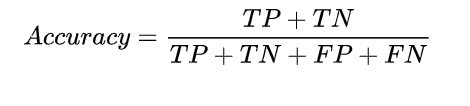
优点:能够判断总的正确率;
缺点:但是在样本不均衡的情况下,并不能作为很好的指标来衡量结果。
案例:比如样本集中,正样本90个,负样本10个,样本是严重不平衡的。对于这种情况,只需要将全部样本预测为正样本,就能够得到90%的准确率,但是完全没有意义。对于新数据,完全体现不出准确率。因此,在样本不平衡的情况下,得到的高准确率没有任何意义,此时准确率就会失效。(可以使用AUC(AreaUnder roc Curve)值来度量算法好坏,在不平衡数据分类中最常用的指标之一)
2.3 精确率(Precision)
精准率(Precision)又叫查准率,它是针对预测结果而言的,它的含义是在所有被预测为正的样本中实际为正的样本的概率,意思就是在预测为正样本的结果中,我们有多少把握可以预测正确,其公式如下:
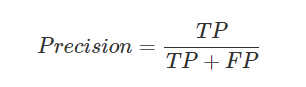
**应用场景:**比如在商品推荐系统中,希望更精准的了解客户需求,避免推送用户不感兴趣的内容;
2.4 召回率(Recall)
召回率(Recall)又称查全率,它是针对原样本而言的,它的含义是在实际为正的样本中被预测为正样本的概率,其公式如下:
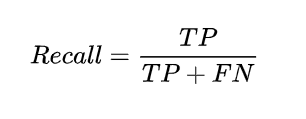
精确率与召回率的应用场景: 例如,在预测股票的时候,更关心Precision,即预测升的那些股票里,真的升了有多少,因为那些预测升的股票都是投钱的。而在预测病患的场景下,更关注Recall,即真的患病的那些人里预测错了情况应该越少越好。
Precision和Recall是一对大多数情况下是此消彼长的度量。 例如在推荐系统中,想让推送的内容尽可能用户全都感兴趣,那只能推送把握高的内容,这样就漏掉了一些用户感兴趣的内容Recall就低了(这里比较迷糊是为什么Recall就降低了呢,比如你预测一个视频内容,用户感兴趣的概率为0.7,你设置概率达到0.8以上才放心将内容推给用户,这样会导致TP降低,FN上升,一定程度上Recall会降低);如果想让用户感兴趣的内容都被推送,那只有将所有内容都推送上,宁可错杀一千,不可放过一个 (此时,当将不感兴趣的内容越多,FP越大,一定情况下,这样Precision就会降低了) 。
2.5 F1 Score
Precision和Recal指标大多数情况下是此消彼长的度量,即精准率高了,召回率就下降,在一些场景下要兼顾精准率和召回率,最常见的方法就是F-Measure,又称F-Score。F-Measure是P和R的加权调和平均,即:
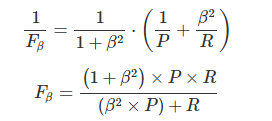
特别地,当β=1时,也就是常见的F1-Score,是P和R的调和平均,当F1较高时,模型的性能越好:

from sklearn.metrics import f1_score, precision_score, recall_score
y_true=[1,2,3]
y_pred=[1,1,3]
f1 = f1_score( y_true, y_pred, average='macro' )
p = precision_score(y_true, y_pred, average='macro')
r = recall_score(y_true, y_pred, average='macro')
print(f1, p, r)
2.6 ROC曲线
AUC的优点:
1.不受正负样本比例的影响
2.适合于排序业务,主要衡量一个模型的排序能力
AUC的缺点:
1.没有关注模型预测的具体概率值
2.无法反应正样本内部的排序能力以及负样本内部的排序能力
参考
https://www.cnblogs.com/guoyaohua/p/classification-metrics.html
https://baijiahao.baidu.com/s?id=1682575810834946835&wfr=spider&for=pc
https://zhuanlan.zhihu.com/p/258596465
https://www.cnblogs.com/guoyaohua/p/classification-metrics.html
https://www.cnblogs.com/guoyaohua/p/classification-metrics.html
https://zhuanlan.zhihu.com/p/431849072