范数
机器学习模型中,常加入惩罚项(结构风险),防止过拟合。
L0范数
L0范数指向量中非零元素的个数,直观上来说使用L0范数即想让模型参数为零的元素尽可能的多,或者说是为了参数稀疏。但是L0范数很难求导或者优化。
L1范数
L1范数指向量中各个元素的绝对值之和,也称“稀疏规则算子”,使用率较高,是L0范数的最优凸近似。
补充:
任何的规则化算子,如果他在Wi=0的地方不可微,并且可以分解为一个“求和”的形式,那么这个规则化算子就可以实现稀疏。L1范数即符合。
L2范数
L2范数是向量中各个元素的平方的和,称为"岭回归"。一定程度上能够避免过拟合(每个参数都非常小,也就是如果数据变动不会造成太大的扰动)
数学推导
L1&L2范数

如图所示,分别为线性回归添加1、L2范数的等高线示意图,可以看出L1范数倾向于产生值为0的交点,所以L1范数能产生稀疏的结果,而L2范数倾向于接近于零。
从贝叶斯的角度
(贝叶斯派认为参数不是固定的,是一个随机变量,服从某个分布)
L1正则相当于加了Laplacean先验,L2正则项相当于加入了Gaussian先验。
参考
trace Lasso范数
1.已有研究表明L1范数在处理高维低相关数据时效果很好,但是面对相关数据时,L1范数通常会在相关的变量中随机选择一个,即不稳定;与此同时,L2范数(线性回归中加入L2范数叫岭回归)会两个都选择,但是L2范数为强凸,某些变量可能不需要强凸性,且L2在稀疏性上不如L1范数;
2.group Lasso是基于Lasso的改进,公式如下:
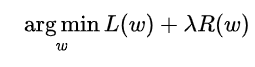
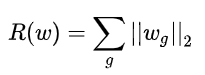
将所有参数w分为N组,对每一组内部使用L2范数,也就是上图和式的每一项,形成一个N元向量,然后继续在这N元 向量使用L1范数,也就是上图式子的加和,(由于L2范数大于等于零,所以无需加绝对值了,从而得到最终形式),group lasso的意义在于,可以成组的赋予0,适用于某些现实场景,但是如何确定分组仍是一个难以解决的问题。
3.
trace Lasso范数是介于L1范数与L2范数之间,取决于相关性,当所有特征正交时,等价于L1范数;当特征高度相关甚至是相等时,等价于L2范数。
稀疏
稀疏这个概念,在稀疏编码,非负矩阵分解等很想多地方都有见过,寻求稀疏的意义主要有以下几点:
1.可解释性(很多文献都有提到)
稀疏使得某些参数为0,即去除了部分特征,便可以理解为这些去除的特征与目标关系不大,相反,可以对留下的特征进行进一步的分析。
2.常用于降维,更简介的表示信息,且方便后续处理
参考文献
【Trace Lasso: a trace norm regularization for correlated designs】