介绍
英文题目:Semi-Supervised Classification with Graph Convolutional Networks
中文题目:使用卷积图神经网络实现半监督分类器
论文地址:https://arxiv.org/abs/1609.02907
领域:自然语言处理,知识图谱,图神经网络
上传时间:2016
出处:ICLR 2017
被引量:10671
代码和数据:
- https://github.com/tkipf/gcn
- https://github.com/kaize0409/pygcn/
阅读时间:22-03-11
#自然语言处理 #知识图谱
泛读
- 针对问题:图节点多分类,半监督学习
- 结果:在知识图和引文图数据集中,有效提升了精度和效率
- 核心方法:基于频谱图,卷积神经网络,编码时考虑到图结构和节点的特征
- 难点:几乎全是公式推导,先验知识太多,单看公式看不懂
- 泛读后理解程度:30%
(看完题目、摘要、结论、图表及小标题)
精读
摘要
论文提出了基于图的,使用类似卷积神经网络的半监督学习方法。选择卷积结构让我们在建模时更注重邻近的节点。模型隐藏层编码同时考虑了局部结构和节点特征。相较于之前模型效果明显提升。
1. 介绍
论文主要解决图中节点的分类问题,且只对图中部分节点打了标签,使用半监督学习方法,通过显式的基于图的规则的方式打标签。在损失函数中使用了拉普拉斯正则化项:
L
=
L
0
+
λ
L
r
e
g
(
1
)
L=L_0+\lambda L_{reg}\qquad (1)
L=L0?+λLreg?(1)
其中:
L
r
e
g
=
∑
i
,
j
A
i
j
∣
∣
f
(
X
i
)
?
f
(
X
j
)
∣
∣
2
=
f
(
X
)
T
Δ
f
(
X
)
L_{reg}=\sum_{i,j}A_{ij}||f(X_i)-f(X_j)||^2=f(X)^T\Delta f(X)
Lreg?=i,j∑?Aij?∣∣f(Xi?)?f(Xj?)∣∣2=f(X)TΔf(X)
其中L0是有标签部分的误差(分类的类别),λ是正则化项的权重Lreg通过所有数据(含有标签和无标签)计算得出;把神经网络编码作为函数f,X是节点的原始的特征矩阵。
Δ
=
D
?
A
\Delta=D-A
Δ=D?A,其中A是领域矩阵(其值可以是0/1值,也可以是权重),D是度矩阵,? 是拉普拉斯矩阵,有时也用符号L表示。
预备知识
邻接矩阵
定义权重Aij为点vi和点vj之间的权重,所有点间线的权重Aij组成邻接矩阵A,第i行第j值表示为Aij。
度矩阵
定义di是与i点相连所有点的权重之和:
d
i
=
∑
j
=
1
n
A
i
j
di = \sum_{j=1}^n A_{ij}
di=j=1∑n?Aij?
度矩阵D是一个对角矩阵(主对角线上有值):
D
=
(
d
1
.
.
.
.
.
.
.
.
.
d
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
d
n
)
D=\left(\begin{matrix} d1 & ... & ...\\ ... & d2 & ...\\ ... & ... & ... \\ ... & ... & dn\end{matrix} \right)
D=?????d1.........?...d2......?.........dn??????
拉普拉斯矩阵
L = D ? A L=D-A L=D?A

拉普拉斯算子
拉普拉斯矩阵就是图结构上的拉普拉斯算子,或者说是离散的拉普拉斯算子。
拉普拉斯算子对应的运算是:二阶导数,即散度。它用于衡量一个节点变化之后,对其他相邻结点(也可以说是整个图)的干扰总收益(总变化):将所有相邻的点相加再减去该中心点x的相邻个数。
Δ
f
=
∑
?
f
?
2
x
\Delta f= \sum \frac{\partial f}{\partial^2x}
Δf=∑?2x?f?
离散函数的一阶导(含义是:一个节点与它邻近节点的差异):
?
f
?
x
=
f
′
(
x
)
=
f
(
x
+
1
)
?
f
(
x
)
\frac{\partial f}{\partial x}=f'(x)=f(x+1)-f(x)
?x?f?=f′(x)=f(x+1)?f(x)
离散函数的二阶导(一个节点与它前后两个点组成的关系,是平滑还是尖峰)
?
f
2
?
x
2
=
f
′
′
(
x
)
≈
f
′
(
x
+
1
)
?
f
′
(
x
)
=
f
(
x
+
1
)
+
f
(
x
?
1
)
?
2
f
(
x
)
\begin{aligned} \frac{\partial f^2}{\partial x^2}&=f''(x) \approx f'(x+1)-f'(x) \\ &=f(x+1)+f(x-1)-2f(x) \end{aligned}
?x2?f2??=f′′(x)≈f′(x+1)?f′(x)=f(x+1)+f(x?1)?2f(x)?
对于某一个点i,
Δ
f
i
=
∑
j
∈
N
i
(
f
i
?
f
j
)
\Delta f_i=\sum_{j\in N_i}(f_i-f_j)
Δfi?=j∈Ni?∑?(fi??fj?)
如果边具有权重Aij,则有:
Δ
f
i
=
∑
j
∈
N
i
A
i
j
(
f
i
?
f
j
)
\Delta f_i=\sum_{j\in N_i}A_{ij}(f_i-f_j)
Δfi?=j∈Ni?∑?Aij?(fi??fj?)
当i,j无边相连时,Aij=0,所以Ni就可以变成N。
Δ
f
i
=
∑
j
∈
N
A
i
j
(
f
i
?
f
j
)
=
∑
j
∈
N
A
i
j
f
i
?
∑
j
∈
N
A
i
j
f
j
=
d
i
f
i
?
A
i
:
f
\begin{aligned} \Delta f_i & =\sum_{j\in N}A_{ij}(f_i-f_j) \\ & =\sum_{j\in N}A_{ij}f_i -\sum_{j\in N}A_{ij}f_j \\ & = d_if_i-A_{i:}f \end{aligned}
Δfi??=j∈N∑?Aij?(fi??fj?)=j∈N∑?Aij?fi??j∈N∑?Aij?fj?=di?fi??Ai:?f?
空间的二阶导:
Δ
f
=
∑
?
f
?
2
x
=
(
A
?
D
)
f
=
L
f
\Delta f= \sum \frac{\partial f}{\partial^2x}=(A-D)f=Lf
Δf=∑?2x?f?=(A?D)f=Lf
正文
正则化项Lreg的目标是让有连接的点在编码后差异足够小,整个图更平滑。该公式一依赖假设:图中连通的节点共享相同标签,这限制了模型的表述能力,因为边不只用于编码节点的相似性。
使用神经网络对图结构编码,用节点特征X、邻接矩阵A和函数f编码:f(X,A),利用有标签和无标签数据共同训练模型,使模型能够学习到对所有节点均适用的规则。
本文贡献:
- 介绍了一种简单而有效的神经网络模型分层规则,它使用图谱卷积的一阶近似。
- 示范了用半监督学习的,基于图的神经网络方法,解决图节点分类问题,模型的精度和效率方面相较于SOTA都有显著提升。
2. 图的快速近似卷积
对于图神经网络f(X,A),文中提出了多层图卷积网络(GCN),下图展示了基于层的递推,每个隐藏层计算如下:
H
(
l
+
1
)
=
σ
(
D
~
?
1
2
A
~
D
~
?
1
2
H
(
l
)
W
(
l
)
)
(
2
)
H^{(l+1)}=\sigma(\widetilde{D}^{-\frac{1}{2}}\widetilde{A}\widetilde{D}^{-\frac{1}{2}}H^{(l)}W^{(l)}) \qquad(2)
H(l+1)=σ(D
?21?A
D
?21?H(l)W(l))(2)
其中
A
~
=
A
+
I
N
\widetilde{A}=A+I_N
A
=A+IN?,A是邻接矩阵,它表示了节点与其邻居的相关信息,
I
N
I_N
IN?是单位矩阵(对角线全1其它为0),它补充了该节点自身的信息。计算度矩阵
D
~
i
i
=
∑
j
A
~
i
j
\widetilde{D}_{ii}=\sum_j\widetilde{A}_{ij}
D
ii?=∑j?A
ij?,也考虑了节点自身的信息。
W
(
l
)
W^{(l)}
W(l)是对不同层分别训练的权重参数。 σ是激活函数。H为隐藏层,H(0)=X。
2.1 谱图卷积
预备知识
卷积
- 卷积(Convolution)是通过两个函数f和g生成第三个函数的一种数学算子。
- CNN中卷积是离散卷积,两个函数分别是卷积核和图片像素值,它实现了对图片的局部连接和参数共享。
- 图卷积:拓扑图中每个顶点的相邻顶点数目都可能不同,某个点可能与所有点都有连接,也可能部分连接,所以没办法用直接用卷积核过滤某一部分;因此,需要借助拉普拉斯矩阵实现卷积。
特征分解
机器学习_用PCA主成分分析给数据降维#1 特征值与特征向量
傅里叶变换
傅里叶变换是一种投影,比如将函数拆解成无数个不同频率正弦波之和。
空间傅里叶变换:一个N 维空间,只要找到该空间的基,该空间的任意向量就都可以由正交基线性组合。
函数傅里叶变换:将一个函数展开成正交函数基的线性组合。
图的傅里叶变换:在图上找正交基,图上任意点可表示为正交基的线性组合。
因此,只要找到图的正交基,就可以完成图的傅里叶变换,再由卷积定理,就可以实现对图的卷积。
卷积定理
函数卷积的傅里叶变换是函数傅立叶变换的乘积。
f
?
g
=
F
?
1
{
F
(
f
)
?
F
(
g
)
}
f\star g=F^{-1}\{F(f)\cdot F(g)\}
f?g=F?1{F(f)?F(g)}
求卷积就变成了,两个函数分别做傅里叶变换,相乘后,再反向傅里叶变换即可。
图的频域变换步骤
- 创建图的表征矩阵
- 特征分解:计算矩阵的特征值和特征向量;通过特征向量将节点从空间映射到频域(拉普拉斯矩阵是对称的,所以可以进行对角化,也就是找到正交基)
- 进行下一步操作:基于新的表征,进行聚类或分类……
L = U Λ U T = ( u 1 , u 2 , . . . , u n ) ( λ 1 ? λ n ) ( u 1 u 2 . . . u n ) L=U\Lambda U^T=(u_1,u_2,...,u_n)\left( \begin{matrix} λ1 & & \\ & ? & \\ & & λn \end{matrix} \right) \left( \begin{matrix} u_1\\ u_2\\ ... \\ u_n \end{matrix} \right) L=UΛUT=(u1?,u2?,...,un?)???λ1???λn?????????u1?u2?...un???????
特征向量U,特征值 Λ = { λ 1 , λ 1 , … , λ n } \Lambda= \{\lambda_1,\lambda_1,\ldots,\lambda_n\} Λ={λ1?,λ1?,…,λn?}, u l u_l ul? 是对应于 λ l \lambda_l λl? 的基。设特征值从大到小是 λ 1 \lambda_1 λ1?到 λ n \lambda n λn,其中 λ 1 \lambda_1 λ1?影响最大,那么保留前k个 λ \lambda λ就可以大致逼近原来L。
图傅里叶变换是在将一个图信号分解到不同平滑程度的图信号上,就像传统傅里叶变换将函数分解到不同频率的函数上一样。
图傅里叶变换将图信号往拉普拉斯特征向量上投影,也是一种信号分解。如果将图看作信号的函数,把对图中节点的操作f(i)映射成了频域的 f ^ ( λ 1 ) \hat{f}(\lambda_1) f^?(λ1?),其中i是节点, λ 1 \lambda_1 λ1?是特征值,把对节点的变换变成了对特征值的变换。 f ^ \hat{f} f^?是对整体的变换。
正文
由于无法直接在图上进行卷积操作,如果想实现卷积,需要借助拉普拉斯矩阵。经过变换,图中所有节点的特征都可以被图的拉普拉斯矩阵的特征向量的线性组合表示。
图卷积需要使用卷积核gθ缩放每个节点(公式3左边),公式右边的gθ是对特征值的卷积,θ为参数,其个数和图中节点个数相同:
g
θ
?
x
=
U
g
θ
U
T
x
(
3
)
g_\theta \star x=Ug_\theta U^Tx \qquad (3)
gθ??x=Ugθ?UTx(3)
这里 x 是图中节点的输入向量,左边的星指卷积,即对 x 的卷积,U 是拉普拉斯矩阵的特征向量(图的正交基), Λ是特征值组成的对角矩阵,
U
T
x
U^Tx
UTx是对x的傅里叶变换。可将右侧的gθ看成对拉普拉斯矩阵特征值的函数,即
g
θ
(
Λ
)
g\theta(\Lambda)
gθ(Λ)。如果想使用式3,需要对L做特征分解得到U,计算量是
O
(
N
2
)
O(N^2)
O(N2),对大图来说计算量太大。此时:
g
θ
(
Λ
)
g_\theta(\Lambda)
gθ?(Λ)是一阶的情况,它只考虑节点的一跳之内的近邻,如果需要支持多跳,则还需考虑
Λ
k
\Lambda^k
Λk:
g
θ
(
Λ
)
≈
∑
k
=
0
K
θ
k
Λ
k
g_\theta(\Lambda) \approx \sum_{k=0}^K \theta_k \Lambda^k
gθ?(Λ)≈k=0∑K?θk?Λk
然后,使用了切比雪夫多项式方法逼近
g
θ
(
Λ
)
g\theta(\Lambda)
gθ(Λ)函数,它通过设置k值只关注k跳内的关系。
g
θ
′
(
Λ
)
≈
∑
k
=
0
K
θ
k
′
T
k
(
Λ
~
)
(
4
)
g_{\theta'}(\Lambda) \approx \sum_{k=0}^K \theta_k'T_k(\widetilde{\Lambda}) \qquad (4)
gθ′?(Λ)≈k=0∑K?θk′?Tk?(Λ
)(4)
这里的
Λ
~
=
2
λ
m
a
x
Λ
?
I
N
\widetilde{\Lambda}=\frac{2}{\lambda_{max}}\Lambda-I_N
Λ
=λmax?2?Λ?IN?,λmax是L矩阵的最大特征值,计算后相当于做了正则化,将特征值映射到[-1,1]之间;θ′ 是切比雪夫系数向量,由切比雪夫不等式的定义可知:
T
k
(
x
)
=
2
x
T
k
?
1
(
x
)
?
T
k
?
2
(
x
)
T_k(x)=2xT_{k-1}(x)-T_{k-2}(x)
Tk?(x)=2xTk?1?(x)?Tk?2?(x)
其中T0(x)=1,T1(x)=x。Tk可以迭代计算,从而降低了计算复杂度。
考虑到文中遇到的现实问题是对x的卷积,代入傅里叶变换,最后简化得到:
g
θ
′
?
x
≈
∑
k
=
0
K
θ
k
′
T
k
(
L
~
)
x
(
5
)
g_{\theta'}\star x \approx \sum_{k=0}^{K}\theta_k'T_k(\widetilde{L})x\qquad(5)
gθ′??x≈k=0∑K?θk′?Tk?(L
)x(5)
同样的
L
~
=
2
λ
m
a
x
L
?
I
N
\widetilde{L}=\frac{2}{\lambda_{max}}L-I_N
L
=λmax?2?L?IN?,问题就变成求解K次多项式问题,它只依赖节点,及与节点最多在K跳内的邻居。其复杂度为O(|E|),E为边数,与边的数据成线性关系。
切比雪夫多项式实现的目标是最佳逼近,它利用以递归方式定义的多项式序列,gθ(Λ)可以用切比雪夫多项式Tk(X)的截断展开式来很好地逼近K阶。
2.2 基于层的线性模型
以下是此论文的优化重点。
对于公式5,如果限制K=1,也就是每个节点只考虑它的一阶邻居,上述函数就变成了拉普拉斯谱频的线性函数(从而不再受切比雪夫多项式的规则限制),将其看作一层,通过堆叠多层,来实现丰富的表达能力。我们希望模型对于较宽的度分布,可以平衡图中局部领域的过拟合;另外,多层机制也可以构建更深的网络,来提升模型在多领域的建模能力。
当K=1时,最大特征向量λmax≈2
g
θ
′
?
x
≈
θ
0
′
x
+
θ
1
′
(
L
?
I
N
)
x
=
θ
0
′
x
?
θ
1
′
D
?
1
2
A
D
?
1
2
x
(
6
)
\begin{aligned} g_{\theta'}\star x & \approx \theta_0'x+\theta_1'(L-I_N)x\\ & =\theta_0'x-\theta_1'D^{-\frac{1}{2}}AD^{-\frac{1}{2}}x \qquad (6) \end{aligned}
gθ′??x?≈θ0′?x+θ1′?(L?IN?)x=θ0′?x?θ1′?D?21?AD?21?x(6)?
这是由于:
L
=
D
?
1
2
(
D
?
A
)
D
?
1
2
=
I
n
?
D
?
1
2
A
D
?
1
2
L=D^{-\frac{1}{2}}(D-A)D^{-\frac{1}{2}}=I_n-D^{-\frac{1}{2}}AD^{-\frac{1}{2}}
L=D?21?(D?A)D?21?=In??D?21?AD?21?
公式5被拆成了两部分,前一部分计算当前节点,后一部分计算领域节点,卷积核可被整个网络共享,连续应用卷积核有效地卷积节点的第k阶邻域,其中k可看作卷积层的数目。
实际应用时,通过限制参数数目,既可以避免过拟合,也可以减少运算量,进而得到以下公式:
g
θ
?
x
≈
θ
(
I
N
+
D
?
1
2
A
D
?
1
2
)
x
(
7
)
g_\theta\star x \approx \theta(I_N + D^{-\frac{1}{2}}AD^{-\frac{1}{2}})x \qquad (7)
gθ??x≈θ(IN?+D?21?AD?21?)x(7)
将参数定义为
θ
=
θ
0
′
=
?
θ
1
′
\theta=\theta_0'=-\theta_1'
θ=θ0′?=?θ1′?,
I
N
+
D
?
1
2
A
D
?
1
2
I_N+D^{-\frac{1}{2}}AD^{-\frac{1}{2}}
IN?+D?21?AD?21? 是[0,2]范围内的特征值,在神经网络上连续使用同一操作可能引起梯度爆炸或梯度消失,使用
I
N
I_N
IN?,将A和D变成了
A
~
\widetilde{A}
A
和
D
~
\widetilde{D}
D
。
根据以上定义,
X
∈
R
N
x
C
X\in R^{NxC}
X∈RNxC,N是节点数,C是输入的特征维度,计算新的节点表征:
Z
=
D
~
?
1
2
A
~
D
~
?
1
2
X
θ
(
8
)
Z=\widetilde{D}^{-\frac{1}{2}}\widetilde{A}\widetilde{D}^{-\frac{1}{2}}X\theta \qquad(8)
Z=D
?21?A
D
?21?Xθ(8)
其中
θ
\theta
θ是参数矩阵,Z输出的信号矩阵。计算复杂度是O(|E|FC),其中F是输出维度,C是输入维度。
3. 半监督的节点分类问题

通过有监督学习,左图:将输入为C维的特征(节点X以及节点间的关系A),编码成输出F维特征(向量表示Z),最终实现分类y。其中黑线表示图的边,它在多层之间共享。右图:用颜色标出结果。
3.1 示例
接下来,以两层的GCN为例,前向传播过程如下式所式:
Z
=
f
(
X
,
A
)
=
s
o
f
t
m
a
x
(
A
^
R
e
L
U
(
A
^
X
W
(
0
)
)
W
(
1
)
)
(
9
)
\begin{aligned} Z &=f(X,A) \\ & =softmax(\hat{A}ReLU(\hat{A}XW^{(0)})W^{(1)}) \qquad (9) \end{aligned}
Z?=f(X,A)=softmax(A^ReLU(A^XW(0))W(1))(9)?
w0是一个CxH的矩阵用于将输入数据转换到隐藏层;W1是HxF的矩阵,用于将隐藏层转换为输出;softmax用于处理最后的多分类,最后用交叉熵作为误差函数:
L = ? ∑ l ∈ y L ∑ j = 1 F Y l f ? l n Z l f ( 10 ) L=-\sum_{l\in y_L}\sum_{j=1}^F Y_{lf}\ lnZ_{lf} \qquad (10) L=?l∈yL?∑?j=1∑F?Ylf??lnZlf?(10)
其中yL是有标签的节点集合。在学习过程中训练W0和W1。
3.2 实现
代码由TensorFlow实现,训练基于GPU环境,计算复杂度是O(|E|CHF)。
4. 相关工作
4.1 基于图的半监督学习
基于图的半监督学习有两大方向:图的拉普拉斯正则化;基于图嵌入的方法。
最近,图嵌入方法进一步被关注,它源于skip-gram模型,DeepWalk通过随机游走学习邻近节点,LINE和node2vec又优化了随机游走(深度/广度优先),还有其它一些图嵌入的优化方法。
4.2 图神经网络
将神经网络应用到图结构,可以追溯到2005年,2009年提出了使用RNN框架,2015年将CNN引入图结构,然后引入度矩阵,本文也进一步利用不同节点的度来规范化邻接矩阵。
2016年提出的使用图神经网络解决节点分类问题,其复杂度较高,是 O ( N 2 ) O(N^2) O(N2)。本文中方法基于2014年提出的谱图卷积神经网络,文中方法提高了大规模网络中的模型的可扩展性和分类性能。
5 实验
5.1 数据集
实验数据包括引文网络和知识图,如表-1所示:
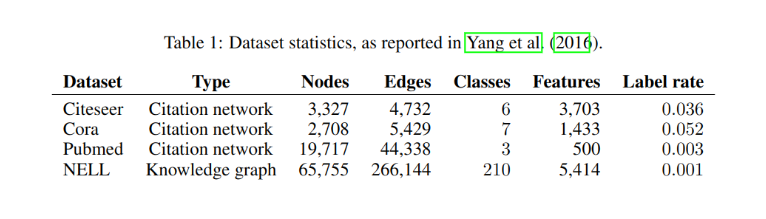
引文网络的输入是用词袋方法提取的每篇文章的词向量,以及文章间的引用关系,用0/1二值表,即无向图,因此邻接矩阵A为对称矩阵。对各篇文章打了类别标签进行训练。NELL知识图是用一组边(关系)连接的实体,实体使用向量表示。
6 ## 结果
6.1 半监督的节点分类
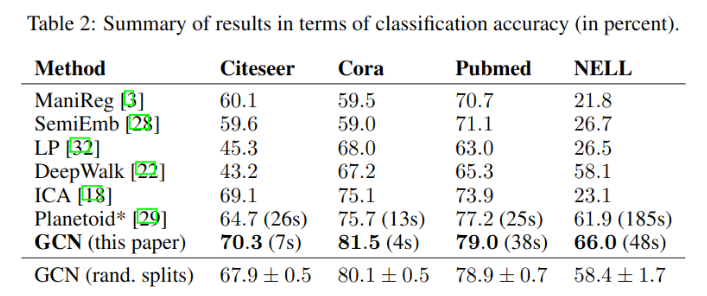
与其它模型比较:
6.2 传播模型评价
使用不同传播模型的效果对比如下:

6.3 每次迭代的耗时

7. 讨论
7.1 半监督模型
文中提出的模型克服了之前模型的两种限制:边仅仅编码节点的相似性;多步pipeline难以被优化的问题。模型效率更高,且提升了分类性能。
实验证明,公式8提出的简化模型,不仅简化了复杂度和参数,还在很多数据集中表现更好。
7.2 局限性和未来的工作
内存
实验中,当图太大时,无法使用GPU计算,只能使用CPU,其时间尚可接受。使用多batch的方法,会把某些领域切断,所以可能影响模型效果。
有向边和边的特征
文中模型目前无法支持边的特征,且只能支持无向图,在实验中处理知识图时,通过对边的处理可以部分解决此问题。
限制假设
论中假设自连接与相邻节点的边同等重要,但对于某些数据集,给其赋予不同权重效果可能更好
A
~
=
A
+
λ
I
N
\widetilde{A}=A+\lambda I_N
A
=A+λIN?
参考
拉普拉斯矩阵与拉普拉斯算子的关系
谱聚类(spectral clustering)原理总结
谱图理论-拉普拉斯矩阵理解
05-spectral 图机器学习之谱分解
神奇的拉普拉斯平滑
图傅里叶变换
《SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS》论文阅读(一)
【图神经网络】图卷积网络 GCN