【生信】全基因组关联分析(GWAS)原理
文章的文字/图片/代码部分/全部来源网络或学术论文,文章会持续修缮更新,仅供大家学习使用。
目录
1.前提知识介绍
1.1 最小二乘法


?
1.2 GWAS的数学原理

?a的最优化为 2.8387, b的最优化为 2.0968 ,公式 y ?= ?2.8387* x ?+ 2.0968
实际上,我们在计算的时候,会加入其他的变量,比如性别,年龄,品系等。这些因素也是影响表型的变量。因此,当考虑其他变量存在时,计算公式会稍微改变一下:y ?= ?ax ?+ zβ ?+ ?b
y:研究的表型
x:基因型数据,这里指每一个SNP
a:SNP的系数
z:年龄,性别等因素
β:年龄,性别等因素的系数
b:残差,除了我们纳入的SNP,性别年龄等因素外等其他可能影响表型的因素;
1.3 Hardy-Weinberg定律&卡方检验

?
1.4 连锁不平衡
在群体遗传学研究中,LD连锁不平衡分析是非常常见的内容,同时也是关联分析的基础。简单理解就是只要两个基因不是完全独立遗传,就会表现出某种程度的连锁,这种情况就叫连锁不平衡。
两个相邻的基因A B, 他们各自的等位基因为a b. 假设A B相互独立遗传,则后代群体中观察得到的单倍体基因型 AB 中出现的P(AB)的概率为 P(A)*P(B)。
但我们实际观察得到群体中单倍体基因型 AB 同时出现的概率为P(AB)。若这两对等位基因是非随机结合的,即两个等位基因是完全独立的,则P(AB)=P(A)*P(B)。
但我们发现实际上P(AB)≠P(A)*P(B),这说明A B是连锁不平衡的。
不平衡程度度量的指标为D:D=P(AB)- P(A) *P(B)
例如位于同一染色体的两个等位基因(AB)同时存在的概率大于人群中因随机分布而同时出现的概率,称这两点处于LD状态。
1.5 曼哈顿图
曼哈顿图(manhattan plot)是一种散点图,通常用于显示具有大量数据点,许多非零振幅和更高振幅值分布的数据。
下图中每个点代表一个SNP,纵轴为每个SNP计算出来的P value取-log10,横轴为SNP所在的染色体,图中对候选位点的分布和数值一目了然。
基因位点的P value越小即-log10(P value)越大,该位点与表型性状或疾病等关联程度越强。
而且通常来说受到连锁不平衡的影响,强关联位点周围的SNP也会显示出相对较高的信号强度,并依次向两边递减,所以会出现上图中红色部分的现象。
一般,在GWAS的研究中,P value的阈值在10^-6 或者10^-8以下。

ggplot标注的SNP

注意:曼哈顿图中,显著的SNP并不是鹤立鸡群的冒出来,而是似乎被捧出来的,就像高楼大厦一样,从底下逐步冒出来的。这一座大厦其实就是连锁在一起的SNP,具有很高的LD score。虽然曼哈顿图里每个点是SNP,但是通常都会把最显著的SNP指向某个基因,因为大家最关注的还是SNP的致病根源,但这样找出来的只有编码区的SNP。
注意:最突出的SNP极有可能不是关键的SNP,它只是临近关键SNP的位点。
?
1.6 箱式图Box-plot
箱形图(Box-plot)是一种用作显示一组数据分散情况的统计图,因形状如箱子而得名。主要用于反映原始数据分布的特征,并且可以进行多组数据分布特征的比较。
箱形图能显示出一组数据的最大值(Maximum)、最小值(Minimum)、中位数(Median)及上下四分位数(1st/3rd Quartile),同时还可以显示逸出值(Outlier)。
?
第一四分位数(Q1),又称较小四分位数,等于该样本中所有数值由小到大排列后第25%的数字。
第二四分位数,又称中位数,等于该样本中所有数值由小到大排列后第50%的数字。
第三四分位数(Q3)又称较大四分位数,等于该样本中所有数值由小到大排列后第75%的数字。
逸出值,是根据四分位间距(interquartile range)进行计算的:
四分位间距= Q3-Q1=ΔQ,在区间 [Q3+1.5ΔQ, Q1-1.5ΔQ] 之外的值即被视为逸出值。
1.7 QQ plot
Q-Q(分位数-分位数)图,是通过将绘制两个概率分布的分位数来比较两者分布关系的图形方法。Q-Q plot可用于比较数据集合或理论分布。
- Q-Q plot就是理论值和实际值的关系图,x=理论值,y=实际值。
- 理想状态下y=x,这些点应该落在y=x这样一条过0点,斜率45度的直线上。
- 如果实际的样本点的值符合的是一般的正态分布,mean=μ,画出的点就应该落在y= x+μ这条直线上,因为此时每个实际的样本点的值,应该就是理论期望值经过 x+μ这样的线性变化得到的。
- 如果样本点确实取自一个正态分布, 那么样本点数量越大,QQplot就越接近一条直线,反之,当样本点数量过少时,QQplot中的点很容易偏离直线。
?
?
2、GWAS的定义
2.1 几个需要知道的概念:
基因型:是指某一生物个体全部基因组合的总称。它反映生物体的遗传构成,即从双亲获得的全部基因的总和。GWAS中主要关注的是全基因组范围上的遗传变异(SNP)。
SNP:SNP单核苷酸多态性是最common的genetic variation类型。
与其并列的还有小的indel(插入或者删除一段小序列,一般在50bp以下)、CNV(基因拷贝数变异)、SV(大的结构变异,一般在50bp以上的长序列的插入、删除、染色体倒位等)。
表型:生物个体可观测的性状。
Allele frequency等位基因频率:每一个基因位点都有两个或多个allele,不同allele之间有明显的频率上的差异,简单点理解就是A和a两个性质的频率,但这里是碱基位点,而不是性状基因。
2.2?全基因组关联分析
全基因组关联分析(Genome wide association study,GWAS)是对多个个体在全基因组范围的遗传变异(标记)多态性进行检测,获得基因型,进而将基因型与可观测的性状,即表型,进行群体水平的统计学分析,根据统计量或显著性 p 值筛选出最有可能影响该性状的遗传变异(标记),挖掘与性状变异相关的基因。
很多地方都是按照上面的一段话定义的,简而言之就是在全基因组范围,研究与目标性状关联的候选基因或基因组区域并进行验证和分析,再进一步解释就是看某个SNP在case和control两个人群间是否有allele frequency的显著差异。
这是我理解的GWAS的大致流程和步骤:

?网上也有人将GWAS的流程图整理如下:

?
基因型数据来源:GWAS通常需要大量的样本,几千是标配,几百就太少,现在有的都达到了几万甚至几十万级别。且GWAS不一定必须做WGS(那太贵了),大部分是做DNA chip即DNA芯片(SNP array),只包含了常见的10^6个SNP。经费多一些会做WES,钱很多的话可以做WGS,编码区和非编码区都检测到。
表型数据来源:表型数据一般是课题研究者前期实验动物群体饲养获得的数据,或者志愿者招募等渠道,网上也有很多共享的数据。
3、GWAS——数据预处理

?
3.1质控的原因:
一般来说,一个人的基因型终其一生几乎不会改变的,因此很少存在同时影响表型又影响基因型的变异。要去除一些可能引起偏差的因素(也就是我们在第一部分中提到的残差),主要有群体结构、个体间存在血缘关系、技术性操作。
?
3.2基因型数据的质控:
排除基因型缺失率高的个体。
排除个体杂合率太高和太低的数据。

?如下图,对于SNP过滤阈值的设定,如哈温伯格-log(P value)、基因型缺失率(call rate)>0.05的样本剔除、MAF值<0.01的SNP位点剔除。

?下图为总结出的几个质量控制需要完成的task,最后,会得出干净的SNP和样本:
| Step | Command | Function |
| Missingness of SNPs | ‐‐geno | 具有很低genotype calls的SNP被剔除。即大部分受试者中都缺失的SNP被排除了。 |
| Missingness of individuals | ‐‐mind | 具有很低genotype calls的个体被剔除。即基因型缺失率过高的个体数据被剔除。 |
| Sex discrepancy | ‐‐check‐sex | 根据 X 染色体杂合/纯合率检查数据集中记录的个体的性别与其性别之间的差异。 |
| Minor allele frequency (MAF) | ‐‐maf | 仅包括高于设置的 MAF(次等位基因频率) 阈值的 SNP。 |
| Hardy–Weinberg equilibrium (HWE) | ‐‐hwe | 排除偏离 Hardy-Weinberg 平衡的标记。 |
| Heterozygosity | 排除个体杂合率太高和太低的数据。 | |
| Relatedness IBD | ‐‐genome | Calculates identity by descent (IBD) of all sample pairs. 计算所有样本对的IBD值。IBD:血源同一。 |
| Relatedness | ‐‐min | 设置阈值并创建相关性高于所选阈值的个人列表。 这意味着可以检测到例如 pi-hat >0.2 相关的受试者(即二级亲属)。 |
| Population stratification IBD | ‐‐genome | 计算所有样本对的IBD值。IBD:血源同一。 |
| Population stratification | ‐‐cluster ‐‐mds‐plot?k | 基于 IBS 生成数据中任何子结构的 k 维表示。 |
?
3.4表型数据质控:
需要对表型数据统计分析:
表型数据为二元——使用逻辑回归
表型数据为连续性变量——使用线性回归
表型数据正态分析(如果不是正态分布,需转换处理为正态分布)
表型数据均值、中值、最大值、最小值,影响因子对表型的影响分析等等。
?这些回归,正态分析,最大最小值,就是很基础的数学处理不做展开。
?
3.5正负链翻转
什么是正负链翻转:在合并数据过程当中,经常会发现不同来源的数据正负链不是统一的。
从个体的角度理解:假如从小明和小红分别拿到了一批基因型数据。那么存在以下几种可能:1)小明的基因型数据统一好正链或者负链;2)小红的基因型数据统一好正链或者负链;3)小明和小红都不知道他们的数据有没有统一好,反正数据拿给你了,你自己解决。
在不知道基因型数据正负链是否统一的情况下,如果直接合并不同来源的数据:
对于大多数突变位点,合并是没有问题的,比如对于A/G,A/C,T/G,T/C突变是可以规避的,但对于A/T,C/G这种突变得到的结果是:对于同一个个体,他在小明的数据库显示的碱基是A,在小红的数据库显示的是T。
从群体的角度理解:对于同一个个体,他在小明的数据库显示的碱基是A,在小红的数据库显示的是T。这就是正负链惹的祸。
解决方法:snpflip软件。本篇blog暂时不涉及实操内容,实操步骤会涉及各项软件、代码和调整参数等,会单独再写一篇。(下面涉及软件实现的)
3.6 基因型填补
定义:基因型填补(genotype imputation),这是处理芯片数据时(前面数据来源部分调到的DNA chip的方法获得的数据),必须走的一个流程。如果你是WGS全基因组测序数据,那么就不需要imputation。
基因型填充的作用是:精确地预测没有被芯片设计所覆盖的SNP位点的基因型,使得更多的遗传位点应用到关联分析中,从而提高发现新的致病基因的可能性。
我的理解:也就是说当我们没钱做很深的测序深度时,有些SNP是被遗漏的,因此需依据模板做基因型填充。这个模板是由高密度SNP构成的单体型(haplotypes)作参考模板。随着千人基因组计划的完成,超过7千万的多态性位点被发现,由此构建了一张丰富的人类遗传单体型图谱,为基因型填充提供了有力依据。
基因型填充的原理概述如下:
- 在具有相同单体型的家系中,遗传标记少的样本可以参照遗传标记多的样本进行基因型填充。
- 对于没有亲缘关系的样本,以上理论也基本适用,主要的差别在于无血缘关系的样本之间共享的单体型比家系样本之间的要短很多。
- 对无亲缘关系样本进行基因型填充需要一个高密度遗传标记构成的单体型图谱作为参照。通过对比待填充样本和参考模板,找到两者之间共有的单体型,然后就可以将匹配上的参考模板中的位点复制到目标数据集中。
- 然而,不是所有的单体型配对都准确一致。当无法准确断定哪一个单体型应该被填充,通常的做法是给出不同单体型出现的概率,并估算不确定性。

上图∶无明显亲缘关系样本的基因体填充简化图。
A输入待研究目标样本和参考模板,
B在目标样本和参考模板之间构建单体型(pre-phasing),
C根据目标样本和参考模板之间共享的单体型进行基因型填充
使用的软件:一个在线网站,Michigan Imputation Server网站链接:
其他的基因型填充软件:

?
3.7群体分层校正
GWAS中通过分析case/control组之间的差异来寻找与疾病关联的SNP位点,然而case和control两组之间,可能本身就存在一定差异,会影响关联分析的检测。
群体分层(Population stratification),是最常见的差异来源,指的是case/control组的样本来自于不同的祖先群体,其分型结果自然是有差异的。
也可以说是:不同群体SNP频率不一样,导致后面做关联分析的时候可能出现假阳性位点(不一定是显著信号位点与该表型有关,可能是与群体SNP频率差异有关),因此我们需要在关联分析前对群体分层校正。
GWAS分析的目的是寻找由于疾病导致的差异,其他的差异都属于系统误差,在进行分析时,需要进行校正。
对于群体分层的校正,通常采主成分分析的方法,即PCA,对应的文章发表在nature genetics上,链接如下:https://www.nature.com/articles/ng1847
常用软件:plink、GCTA,在这里不做实操演示。
4、GWAS——关联分析
下面是GWAS中常用的分析和图表,最重要的两个是曼哈顿图和QQ plot。

?
?画曼哈顿图和QQ plot 首推R包“qqman”,简约方便。
5、GWAS——meta分析
群体分层是GWAS研究中一个比较常见的假阳性来源。也就是说,如果数据存在群体分层,却不加以控制,那么很容易得到一堆假阳性位点。当群体出现分层时,常规手段就是将分层的群体独立分析,最后再做meta分析。前面的群体分层校正是meta分析的前提。
两个常用的软件:
METAL (fixed-effect model) (https://genome.sph.umich.edu/wiki/METAL_Documentation)
METASOFT (random-effect model) (http://genetics.cs.ucla.edu/meta/)
6、GWAS——条件分析
在得到的曼哈顿图中往往发现是一推显著的信号集中在一起。
假设rs121是我们扫出来与某表型最显著相关的位点(P=1.351e-36),rs124尾随其后(6.673e-22),也是与该表型显著相关,那么这个rs124位点是真的与该表型显著相关,还是因为rs124与rs121高度连锁不平衡(linkage disequilibrium),导致我们看到的结果是:rs124永远跟随者rs121水涨船高。为了解决这个问题,我们就需要做条件分析。
一般有两种结果。
(1)条件分析以后,rs124不显著了;这种情况说明rs124是因为rs121才导致信号显著。
(2)条件分析以后,rs124依旧显著;这种情况说明rs124确实与表型相关,跟rs121没有关系。
软件:plink
7、GWAS——gene-based关联分析
gene-based关联分析是SNP-based关联分析的一个补充。
传统意义上的GWAS针对单个SNP位点进行分析,来寻找与疾病或者性状相关联的SNP位点。
然而SNP水平的GWAS分析还存在着一些问题,通常情况下我们根据经验阈值,比如1X10^-6,5X10^-8来筛选统计学显著的SNP位点,这样的做法会过滤到很多p值不够小,即关联效应较弱的基因。对于复杂疾病而言,其易感基因往往是很多关联效用较弱的微效基因构成,这样的筛选方式会漏掉很多重要的信息。
因此,需要尝试在更高水平整合SNP GWAS分析的结果,以提高GWAS检验的效能,一般有gene-based和gene-set-based两种水平。
- gene-based:综合考虑某个基因上多个SNP位点的关联分析结果,来计算该基因与疾病的关联性。一般采用多元线性回归模型,首先对某个基因内所有SNP位点的基因型矩阵进行PCA分析,挑选其中的几个主成分作为回归分析的自变量,通过线性回归来分析与疾病的关联性;
- geneset-based:基因集水平,也可以称之为pathway水平,是基因水平的进阶,考虑了基因生物学功能的关联性,站在生物学功能的角度来研究突变与疾病的关联性。采用self-contained的方法,首先通过一个宽松的阈值,比如0.05来筛选某个基因上的候选SNP位点,在候选SNP位点的基础上,进一步通过严格的阈值来划分类别,比如5X10-8, 划分为显著和非显著两类。然后根据Alleles或者genotypes, 选择对应的模型来计算关联性。

这两种分析是建立在SNP GWAS水平的基础上的,这样方便我们对已有的GWAS分析结果进行二次分析,深入挖掘新的信息。
软件:MAGMA(https://ctg.cncr.nl/software/magma)
8、GWAS——孟德尔随机化分析
Katan1986 提出:不同基因型决定不同的中间表型,若该表型代表个体的某暴露特征,用基因型和疾病的关联效应能够代表暴露因素对疾病的作用,由于等位基因遵循随机分配原则,该作用不受传统流行病学研究中的混杂因素和反向因果关联所影响 (反向因果关联,指的是暴露和结局的时间顺序颠倒)。
?基础研究证实,疾病发生均可追溯到基因水平,即基因型决定中间表型差异,该中间表型代表某暴露因素作用于该疾病。

?
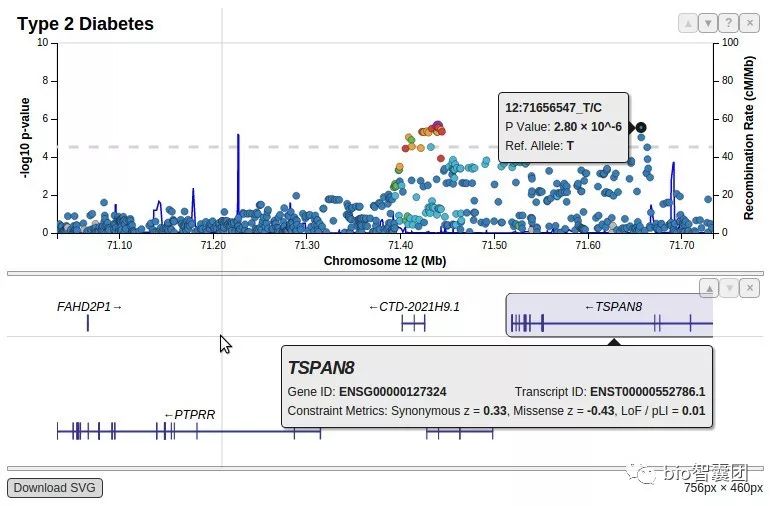
9、GWAS——LocusZoom图
LocusZoom图几乎是GWAS文章的必备图形之一,其主要作用是可以快速可视化GWAS找出来的信号在基因组的具体信息:比如周围有没有高度连锁的位点,高度连锁的位点是否也显著。
下面是locuszoom的示例图:
本篇blog暂时总结至此,期待下一篇能够更深入一点解释和实操GWAS?