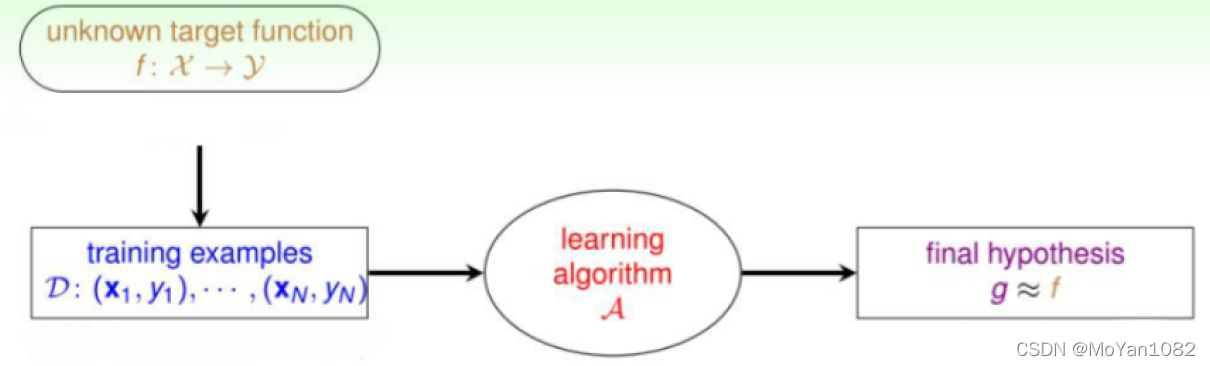
Introduction
Linear regression attempts to get a function g that can use the attributes of the input to predict the resulting output.
g
(
x
i
)
=
w
1
x
1
+
w
2
x
2
+
.
.
.
+
w
m
x
m
+
b
=
w
T
x
+
b
,
?
m
a
k
e
s
?
g
(
x
i
)
?
y
i
g(x_i)=w_1x_1+w_2x_2+...+w_mx_m+b=w^Tx+b, \ makes\ g(x_i)\simeq y_i
g(xi?)=w1?x1?+w2?x2?+...+wm?xm?+b=wTx+b,?makes?g(xi?)?yi?
Obviousely, w,b determine the result of g(x), and our goal is to choice the best w,b to minimize the error.
Ususally, we use MSE(Mean Square Error,
E
=
∑
n
[
y
(
n
)
?
(
w
T
x
(
n
)
+
b
)
]
2
E=\sum_{n}[y^{(n)}-(w^Tx^{(n)}+b)]^2
E=∑n?[y(n)?(wTx(n)+b)]2) as linear regression’s loss funtion. But, why?
Why we use MES as loss function
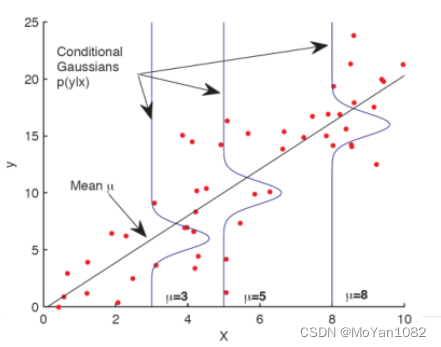
We assume: given x, then the distribution of y satisfies the Gaussian distribution.
Maybe you want to say, there are many kinds of distribution in reality, why Gaussian distribution?
The CLT(central limit theorem) can explain this probelm.
In probability theory, the central limit theorem (CLT) establishes that, in many situations, when independent random variables are summed up, their properly normalized sum tends toward a normal distribution (informally a bell curve) even if the original variables themselves are not normally distributed.
We suppose y satisfies the following Gaussian distribution:
p
(
y
∣
x
)
~
N
(
w
T
x
+
b
,
σ
2
)
p(y | x)\sim N(w^Tx+b,\sigma^2 )
p(y∣x)~N(wTx+b,σ2)
So,
l
o
g
?
l
i
k
e
l
i
h
o
o
d
?
f
u
n
c
t
i
o
n
∝
L
(
w
,
b
)
log-likelihood\ function \propto L(w,b)
log?likelihood?function∝L(w,b), and
L
(
w
,
b
)
=
log
?
(
∏
n
e
x
p
(
?
1
2
σ
2
(
y
(
n
)
?
w
T
x
(
n
)
?
b
)
2
)
)
=
?
1
2
σ
2
∑
n
(
y
(
n
)
?
w
T
x
(
n
)
?
b
)
2
?
w
,
b
=
a
r
g
m
a
x
w
,
b
L
(
w
,
b
)
?
w
,
b
=
a
r
g
m
i
n
w
,
b
∑
n
(
y
(
n
)
?
w
T
x
(
n
)
?
b
)
2
\begin{matrix} L(w,b)&=&\log (\prod_{n}exp(-\frac{1}{2\sigma^2}(y^{(n)}-w^Tx^{(n)}-b)^2)) \\ \\ &=&-\frac{1}{2\sigma^2} \sum_{n} (y^{(n)}-w^Tx^{(n)}-b)^2 \\ \\ \Rightarrow w,b &=& argmax_{w,b}L(w,b) \\ \\ \Rightarrow w,b &=& argmin_{w,b}\sum_n(y^{(n)}-w^Tx^{(n)}-b)^2 \end{matrix}
L(w,b)?w,b?w,b?====?log(∏n?exp(?2σ21?(y(n)?wTx(n)?b)2))?2σ21?∑n?(y(n)?wTx(n)?b)2argmaxw,b?L(w,b)argminw,b?∑n?(y(n)?wTx(n)?b)2?
Is this a bit like Euclidean Distance(geometric meaning)?
That’s why we use MES as loss functoin, and our gold is minnimize it. This also called OSL(Ordinary least squares).
The specific method is to make the partial derivatives with respect to w and b to be 0.
Y
=
[
y
(
1
)
y
(
2
)
?
y
(
n
)
]
X
=
[
x
(
1
)
x
(
2
)
?
x
(
n
)
]
=
[
x
1
(
1
)
?
x
m
(
1
)
x
1
(
2
)
?
x
m
(
2
)
?
x
1
(
n
)
?
x
m
(
n
)
]
b
=
[
b
(
1
)
b
(
2
)
?
b
(
n
)
]
,
?
b
1
=
b
2
=
?
=
b
n
\begin{matrix} Y&=&\begin{bmatrix} y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(n)} \\ \end{bmatrix} \\ X&=&\begin{bmatrix} x^{(1)} \\ x^{(2)} \\ \vdots \\ x^{(n)} \\ \end{bmatrix} &=&\begin{bmatrix} x_1^{(1)} & \cdots & x_m^{(1)} \\ x_1^{(2)} & \cdots & x_m^{(2)} \\ &\vdots & \\ x_1^{(n)} & \cdots & x_m^{(n)} \\ \end{bmatrix} \\ b&=&\begin{bmatrix} b^{(1)} \\ b^{(2)} \\ \vdots \\ b^{(n)} \\ \end{bmatrix} &,&\ b_1=b_2=\cdots =b_n \end{matrix}
YXb?===???????y(1)y(2)?y(n)?????????????x(1)x(2)?x(n)?????????????b(1)b(2)?b(n)????????=,????????x1(1)?x1(2)?x1(n)???????xm(1)?xm(2)?xm(n)??????????b1?=b2?=?=bn??
So, the loss function can be represented as
E
=
(
Y
?
X
w
?
b
)
T
(
Y
?
X
w
?
b
)
E=(Y-Xw-b)^T(Y-Xw-b)
E=(Y?Xw?b)T(Y?Xw?b).
It’s easy to discover that the values of
b
i
b_i
bi? are same, and we can simplify the original function.
We might as well change the representation of w and treat b as a constant weight of 1:
w
=
(
w
1
;
?
?
;
w
n
;
b
)
w=(w_1;\cdots;w_n;b)
w=(w1?;?;wn?;b).
X
=
[
x
(
1
)
;
1
x
(
2
)
;
1
?
x
(
n
)
;
1
]
=
[
x
1
(
1
)
?
x
m
(
1
)
1
x
1
(
2
)
?
x
m
(
2
)
1
?
x
1
(
n
)
?
x
m
(
n
)
1
]
X=\begin{bmatrix} x^{(1)};1 \\ x^{(2)};1 \\ \vdots \\ x^{(n)};1 \\ \end{bmatrix} =\begin{bmatrix} x_1^{(1)} & \cdots & x_m^{(1)} & 1\\ x_1^{(2)} & \cdots & x_m^{(2)} & 1\\ &\vdots & \\ x_1^{(n)} & \cdots & x_m^{(n)} & 1\\ \end{bmatrix}
X=??????x(1);1x(2);1?x(n);1???????=???????x1(1)?x1(2)?x1(n)???????xm(1)?xm(2)?xm(n)??111????????
then,
E
=
(
Y
?
X
w
)
T
(
Y
?
X
w
)
E=(Y-Xw)^T(Y-Xw)
E=(Y?Xw)T(Y?Xw).
Derivations of the loss function
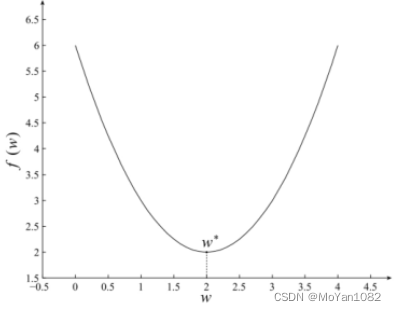
It is easy to discover that E is a convex function, so the optimal solution of function is obtained when the the partial derivative with respect to w is 0.
E
=
(
Y
?
X
w
)
T
(
Y
?
X
w
)
=
(
Y
T
?
w
T
X
T
)
(
Y
?
X
w
)
=
Y
T
Y
?
Y
T
X
w
?
w
T
X
T
Y
+
w
T
X
T
X
w
S
o
,
?
?
E
?
w
=
?
(
Y
T
X
)
T
?
X
T
Y
+
[
X
T
X
+
(
X
T
X
)
T
]
w
=
?
2
X
T
Y
+
2
X
T
X
w
=
?
2
X
T
(
Y
?
X
w
)
\begin{matrix} E&=& (Y-Xw)^T(Y-Xw)\\ \\ &=& (Y^T-w^TX^T)(Y-Xw)\\ \\ &=& Y^TY-Y^TXw-w^TX^TY+w^TX^TXw\\ \\ So,\ \frac{\partial E}{\partial w} &=& -(Y^TX)^T-X^TY+[X^TX+(X^TX)^T]w \\ \\ &=& -2X^TY+2X^TXw \\ \\ &=& -2X^T(Y-Xw) \end{matrix}
ESo,??w?E??======?(Y?Xw)T(Y?Xw)(YT?wTXT)(Y?Xw)YTY?YTXw?wTXTY+wTXTXw?(YTX)T?XTY+[XTX+(XTX)T]w?2XTY+2XTXw?2XT(Y?Xw)?
Then let the partial derivative with respect to w be 0:
X
T
(
Y
?
X
w
)
=
0
X
T
Y
=
X
T
X
w
w
=
[
X
T
X
]
?
1
X
T
Y
\begin{matrix} X^T(Y-Xw) &=& 0 \\ \\ X^TY &=& X^TXw \\ \\ w&=&[X^TX]^{-1}X^TY \end{matrix}
XT(Y?Xw)XTYw?===?0XTXw[XTX]?1XTY?
Obviously, we need to find the inverse of
X
T
X
X^TX
XTX, but it is usually not full-rank matrix or positive definite matrix. Then, you need to use gradient descent, and the source code of sklearn also use gradient descent.
Other than that, you might want to ask why the formula is different from the one in the textbook. So, I hava to say the textbook is real BAD!
Code
X = np.c_[X, np.ones(np.shape(X)[0], 1)]
w_bext = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(Y)
TODO