[人工智能]计算机图形学——直线的生成算法

计算机图形学——直线的生成算法

前言

在计算机中，绘制一条直线是很麻烦的。我们现在常用的显示器是光栅显示器，该显示器下的图像是又一个又一个的点构成的，所以当我们要从A点到B点画一条直线时，是尽可能将A到B两点间的像素点给画出。
下面是几种常见的生成直线的算法

• 数值微分法
• 中点生成直线算法
• Bresenham算法

数值微分法

假设有两点$P_0$ ($x_0$,$y_0$)和$P_1$($x_1$,$y_1$),我们可以通过当前位置($x_i$,$y_i$)分别加上两个小增量$?$*dx,$?$*dy(dx=$x_1$-$x_0$,dy=$y_1$-$y_0$),则有如下两列：
$x_{i+1}$=$x_i$+$?$*dx
$y_{i+1}$=$y_i$+$?$*dy
当$?$足够小时，绘制出的点越多，画出的直线越正规。但设备的精度是有限的，令$?$=$\frac{1}{max(dx,dy)}$
即当k<=1时，有：
$x_{i+1}$=x+1
$y_{i+1}$=y+k
当k>=1时，有
$x_{i+1}$=$x_i$+$\frac{1}{k}$
$y_{i+1}$=$y_i$+1
那为什么要分k>=1和k<1呢？因为“假设最大位移方向是y,而我们每次选取$x_{i+1}$=$x_i$+1,可能会出现y变化过快，导致只绘制出了几个点就画完了，具体的可以动手尝试”
最后，需要注意的是光栅显示上是以一个个像素点为单位的，不可能出现小数点，所以我们要进行四舍五入(四舍五入的方法是+0.5取整)

中点生成直线算法

前面所讲的DDA算法包含浮点数和取整运算，而浮点数的加法比整型加法所需的时间更长，取整运算也不利于硬件的实现，那么怎么进行改进？
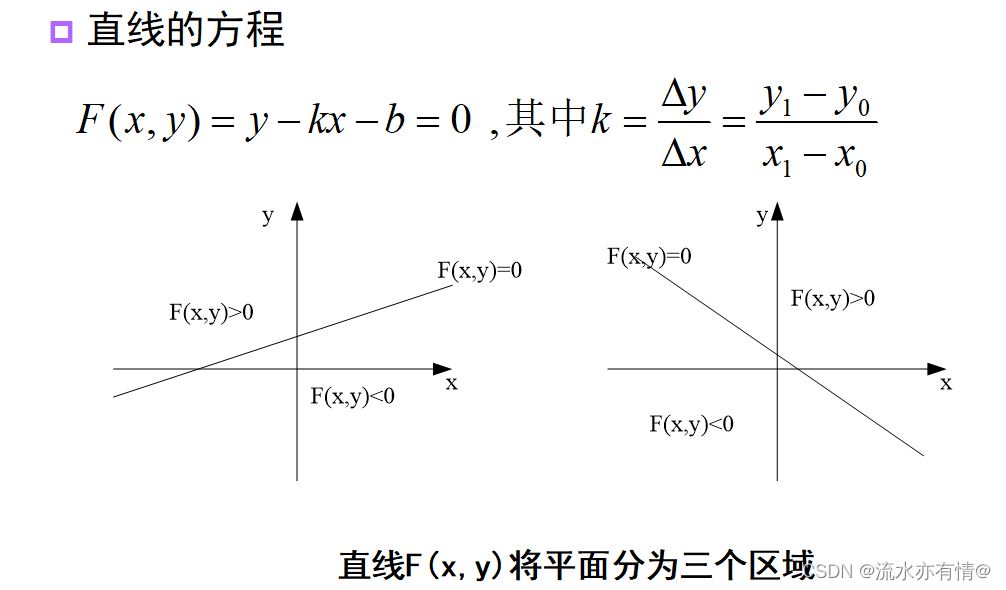
我们可以通过直线方程做文章，上述的直线方程是斜截式。我们中点生成直线算法采用一般式，即F(x,y)=y-kx-b=0,中点生成直线算法的原理是：每次在最大位移方向上走一步，而另一个方向是否走步它取决于实际直线与相邻象素点的距离，这一距离称为误差项

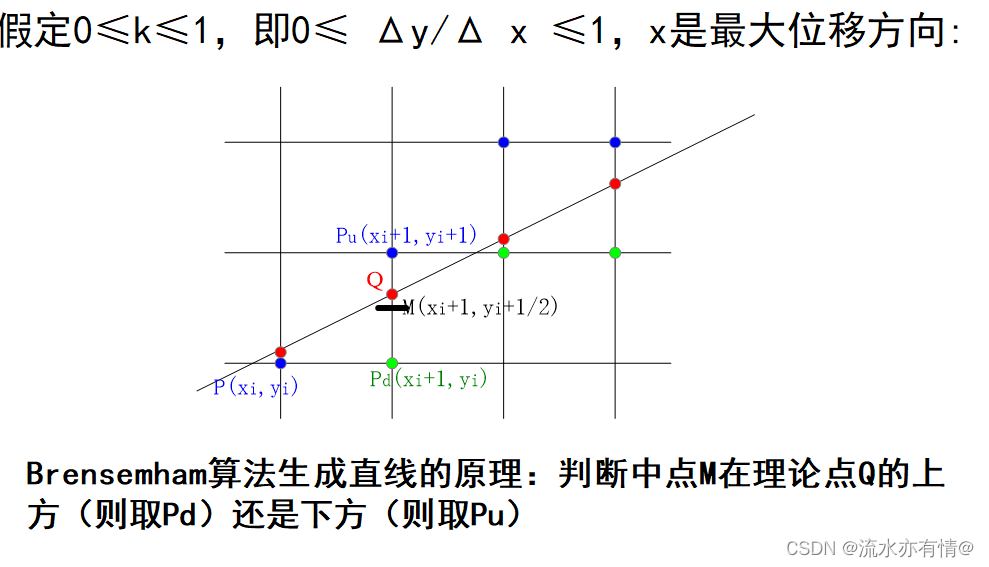
同样给定两点$P_0$ ($x_0$,$y_0$)和$P_1$($x_1$,$y_1$),dx=$x_1$-$x_0$,dy=$y_1$-$y_0$,k=$\frac{dy}{dx}$
假设k<1，因此每次在x方向上+1，y方向上不变或者+1,如上图，假设当前点是P($x_i$,$y_i$),则下一个点应该在$P_u$和$P_d$中二选一，当M在Q点下方时，选上面的点；当M在Q点上方时，Q点离下面点近，选下面的点。
要判断M点在P点上方，只需要把M点带入直线方程，判断它的符号即可。

M点坐标为($x_i$+1,$y_i$+0.5)，构造判别式$d_i$=F($x_m$,$y_m$)=F($x_i$+1,$y_i$+0.5)=$y_i$+0.5-k($x_i$+1)-b,当$d_i$<0时,M在直线下方，y=y+1；当$d_i$>0时,y=y
接下来进行误差项的递推，
①当di<0时，y=y+1，$d_{i+1}$=F($x_i$+2,$y_i$+1.5)=$y_i$+1.5-k($x_i$+2)-k=$d_i$+1-k
②当di>=0时，y=y,$di+1$=F($x_i$+2,$y_i$+0.5)=$y_i$+0.5-k($x_i$+2)-b=$d_i$-k
d0=F($x_0$+1,$y_0$+0.5)=0.5-k
由于我们只需要$d_i$的符号，所以可以用2$d_i$dx来摆脱小数,（整数计算更快）,此时d0’=2d0dx=dx-2dy
综上所述:
①输入直线的两端点P0($X_0$,$Y_0$),P1($X_1$,$Y_1$)。
②计算初始值dx和dy，并计算d0=dx-2dy
③绘制点(x,y)，判断d的符号，如果d<0,(x,y)更新为(x+1,y+1),d更新为d+2dx+2dy；否则(x,y)更新为(x+1,y),d更新为d-2dy
④直线若没有画完，重复步骤③

Bresenham算法

虽然中点Bresenham算法的效率很高，但我们有更直观的改进。我们之前取得是中点，那为什么我们不能把各个像素点构造成网格线？直接看它和网格线下面一点交点距离d大小？若大于0.5，取上面点，反之则取下面点。

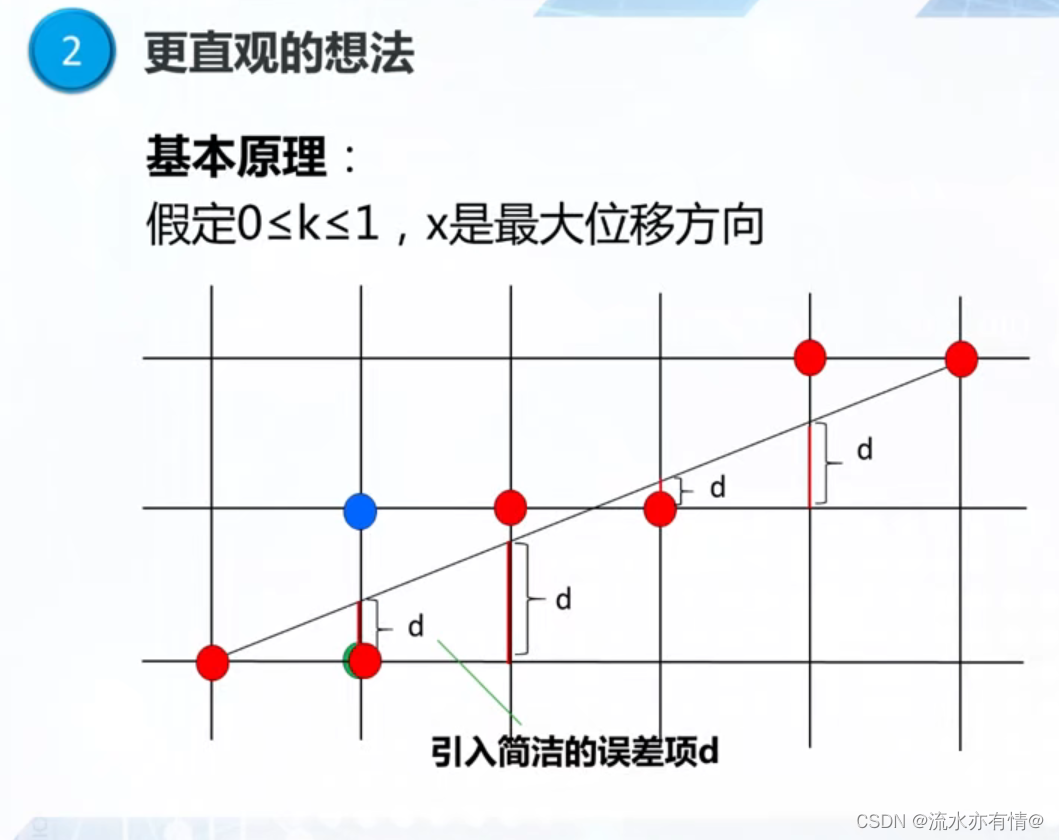
我们仍然假设k<1，则此时有
$x_{i+1}$=$x_i$+1
$y_{i+1}$=$y_i$ 当d<=0.5时
$y_{i+1}$=$y_i$+1 当d>0.5时
相比于中点的Bresenham，d表示更为简洁
故这时候算法的思路是
①d0=0
②$d_{i+1}$=$d_i$+k
③若d>=0.5,d=d-1（注意为什么是0.5而不是1，比如它y+1之后d任大于0.5小于1，下一步又要加一实际上下一步是不用加一的）
直线没绘制完前，重复2，3
这里算法的基本思路就结束了，但前面中点的Bresenham算法只用看符号，而这里d还要与0.5进行比较，故将d=d-0.5
故这时候算法的思路是
①do=-0.5
②$d_{i+1}$=$d_i$+k
③d>=0,d=d-1
但此时的算法仍然有浮点数k，我们按照先前的方法，令d=2didx
故这时候的算法的思路是
①d0=-dx
②$d_{i+1}$=di+2dy
③d>=0，d=d-2dx

综上所述：Bresenham算法的最佳改进为
①输入直线的两端点P0($X_0$,$Y_0$),P1($X_1$,$Y_1$)。
②计算初始值dx和dy，并计算d=-dx
③绘制点(x,y)
④d更新为d+2dy,判断d的符号，如果d>0,(x,y)更新为(x+1,y+1)，同时将d更新为d-2dx；否则(x,y)更新为(x+1,y)
⑤直线若没有画完，重复步骤③④