本部分内容介绍一些特殊的凸优化问题,包括线性规划、二次规划等。
线性规划(LP)(目标和约束函数都是仿射函数):
因为约束函数是线性函数,线性规划问题的可行集是多面体,几何意义如下图所示:
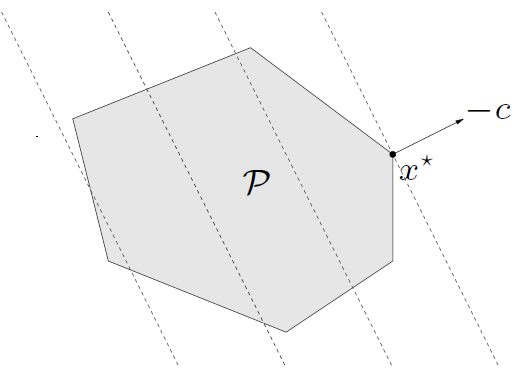
垂直于c的 超平面。
?二次规划(QP)(目标函数是(凸)二次函数,约束函数是仿射函数):
因为约束函数是线性函数,二次规划问题的可行集是多面体,几何意义如下图所示:
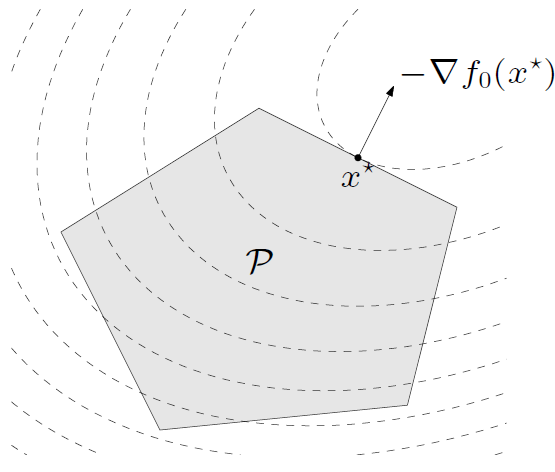
?线性规划问题是二次规划问题的特例,令。著名的例子是最小二乘问题。
二次约束二次规划(QCQP)(目标函数是二次函数,不等式约束函数是二次函数,等式约束函数是仿射函数):
二次约束二次规划问题的可行集是个椭球的交集。(这是因为我们可以通过消除等式得到等价的凸优化问题,该问题只含有不等式约束,其中约束函数是二次函数。)
二次规划问题是二次约束二次规划问题的特例,令。
二阶锥规划(SOCP)(目标函数是仿射函数,不等式约束是二阶锥约束):
下面简单介绍下二阶锥。二阶锥是关于欧几里得范数的范数锥,。二阶锥约束要求仿射函数
位于二阶锥中。因为仿射函数是保凸运算,所以二阶锥约束确定的
可行集也是凸集。
当,二阶锥规划问题变为(目标函数是仿射函数的)二次约束二次规划问题;线性规划问题是二阶锥规划问题的特例,令
。著名的例子是鲁棒线性规划问题。
?广义不等式约束的凸优化问题(在不等式约束中使用广义不等式):
和普通凸优化问题不同,广义不等式约束的凸优化问题中的不等式约束函数的函数值是向量,是
-凸的。
普通凸优化问题的一些结果对于广义不等式约束的凸优化问题同样成立,例如可行集和最优集是凸集、局部最优解也是全局最优解等。和普通凸优化问题一样,我们可以轻松求解广义不等式约束的凸优化问题。
锥规划问题(目标函数是仿射函数,不等式约束函数是仿射函数且-凸的)是一种特殊的广义不等式约束的凸优化问题:
线性规划问题是锥规划问题的一种特例,令非负象限。
半定规划问题是锥规划问题的一种特例,令对称正半定矩阵:
二阶锥规划问题是锥规划问题的一种特例,令,
上的二阶锥: