[人工智能]【pytorch学习实战】线性回归

1. 理论

假设给定下列一组数据集：
D a t a = { ( x 1 , y 1 ) , . . . , ( x n , y n ) } Data = \{(x_1,y_1), ... , (x_n, y_n)\} Data={(x1?,y1?),...,(xn?,yn?)}
希望找到一个函数$f(x)$满足$f(x_i)=w{x}_i+b$，并且$f(x_i)$与$y_i$尽可能的接近，我们使用下列函数(损失函数，Loss Function)来衡量误差：
$$Loss=\sum _{i=1}^m(f(x_i)?y_i{)}^2$$
因为误差有正数，也有负数，所以取平方，这就是注明的均方误差。

2. 代码实例

下列示例的步骤：

1. 数据生成：生成y=3x+10的数据，并携带一定的误差(torch.rand)
2. 数据显示：使用matplotlib画出原始数据
3. 自定义模型：使用nn.Linear(1,1)指定输入输出的维度。
4. 损失函数和优化器的选择：MSE损失和SGD优化器。
5. 开始训练：迭代num_epochs。
6. 显示结果：显示最终的线性回归效果。

import torch
import matplotlib.pyplot as plt
 
 #------------------------制造数据y=3x+10+误差-----------------------------
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)
y = 3*x + 10 + torch.rand(x.size())
 
 #------------------------显示原始数据----------------------------
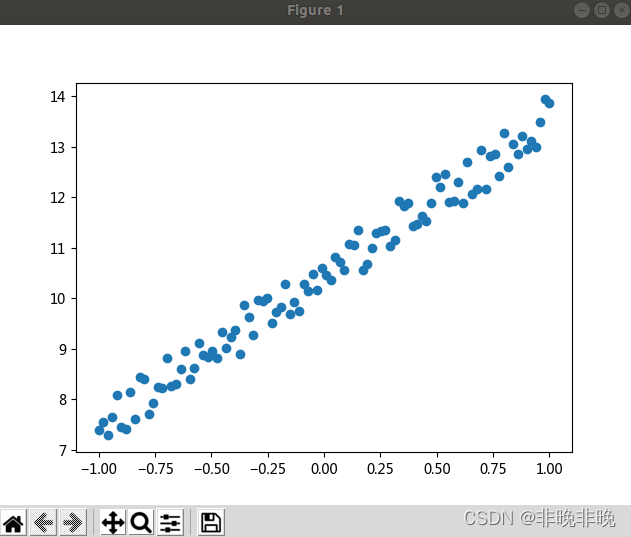
plt.scatter(x.data.numpy(), y.data.numpy())
plt.show()

 #------------------------自定义模型----------------------------
class LinearRegression(torch.nn.Module):
    def __init__(self):
        super(LinearRegression, self).__init__()
        self.linear = torch.nn.Linear(1, 1) # 输入和输出的维度都是1
    def forward(self, x):
        out = self.linear(x)
        return out

  #------------------------选择GPU还是CPU----------------------------
if torch.cuda.is_available():
    model = LinearRegression().cuda()
else:
    model = LinearRegression()

  #------------------------损失函数、优化器的选择----------------------------
criterion = torch.nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=1e-2)

  #------------------------开始训练----------------------------
num_epochs = 1000
for epoch in range(num_epochs):
    if torch.cuda.is_available():
        inputs = x.cuda()
        target = y.cuda()
    else:
        inputs = x
        target = y
 
    # 向前传播
    out = model(inputs)
    loss = criterion(out, target)
 
    # 向后传播
    optimizer.zero_grad() # 注意每次迭代都需要清零，不然梯度会累加到一起造成结果不收敛
    loss.backward()
    optimizer.step()
 
    if (epoch+1) %100 == 0:
        print('Epoch[{}/{}], loss:{:.6f}'.format(epoch+1, num_epochs, loss.item()))#打印数据

  #------------------------测试----------------------------
model.eval() #测试模式
if torch.cuda.is_available():
    predict = model(x.cuda())
    predict = predict.data.cpu().numpy()
else:
    predict = model(x)
    predict = predict.data.numpy()

plt.plot(x.numpy(), y.numpy(), 'ro', label='Original Data')
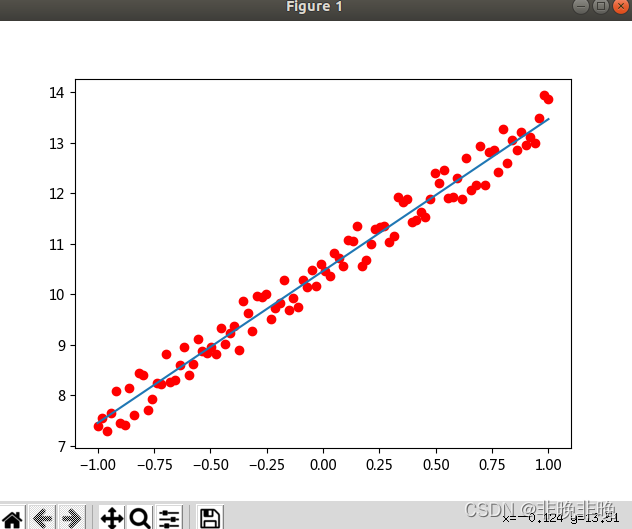
plt.plot(x.numpy(), predict, label='Fitting Line')
plt.show()

原始数据如下：

打印的Epoch和Loss如下：

Epoch[100/1000], loss:3.344052
Epoch[200/1000], loss:0.435524
Epoch[300/1000], loss:0.157943
Epoch[400/1000], loss:0.095231
Epoch[500/1000], loss:0.079358
Epoch[600/1000], loss:0.075307
Epoch[700/1000], loss:0.074272
Epoch[800/1000], loss:0.074008
Epoch[900/1000], loss:0.073940
Epoch[1000/1000], loss:0.073923

最终线性回归效果如下：