正则逼近

正则逼近问题可以写成：
? $\text{minimize}~ \|Ax-b\|+\gamma \phi(x), \gamma>0$
正则逼近问题最小化范数 $\|Ax-b\|$ 和 $\phi(x)$ 的加权和，其中 $\|Ax-b\|$ 测量残差的大小， $\phi(x)$ 是正则项。如果 $\phi(x)$ 是凸函数，则正则逼近问题是凸优化问题。

?两种常见的 $\phi(x)$ 是 $\|x\|$ （测量 $x$ 的大小）和 $\|Dx\|$ （测量x的平滑度），其中? $D$ 代表差分或二阶差分算子。

信号重建/降噪?

一个特殊的正则逼近问题是信号重建/降噪。信号重建/降噪的目的是从采样的含噪观测信号 $y = x + v$ 中估计原始信号 $x$ 。我们假设原始信号 $x$ 是缓慢变化的，而噪声信号 $v$ 是快速时变的，则信号重建/降噪问题可以写成：
? $\text{minimize}~ \|Ax-b\|_2+\gamma \|Dx\|, \gamma>0$
?正则项 $\|Dx\|$ 常用的两种范数?是 $l_2$ 范数（二次平滑）和 $l_1$ 范数（全变差（Total Variation, TV）重建/平滑）。

示例（比较了两种范数的区别）

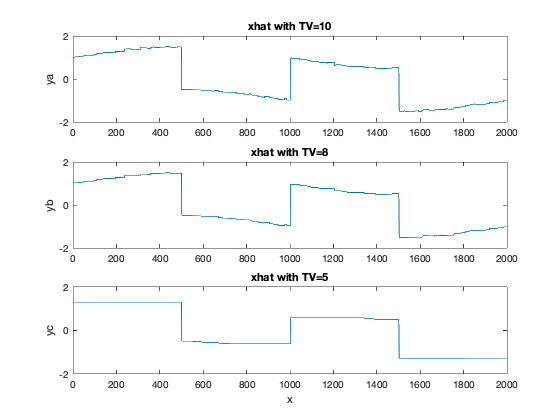
假设原始信号 $x$ 绝大多处是平滑的，但是存在一些跳变；噪声是快速变化的。如果我们采用二次平滑（ $l_2$ 范数）的方法降噪，则无法保留原始信号的跳变；如果我们采用全变差重建（ $l_1$ 范数）的方法降噪，可以在降噪的同时保留原始信号的跳变。代码如下：

% Figure 2 shows the tradeoff curve obtained when varying lambda
% and figure 3 shows three reconstructed signals with different
% total variation.
%
% Figure 4 is a tradeoff curve for quadratic smoothing, while figure 5
% shows three reconstructed signals with quadratic smoothing.
% Note how TV reconstruction does a better job of preserving the
% sharp transitions in the signal while removing the noise.

n = 2000;  % 信号长度
t = (0:n)';

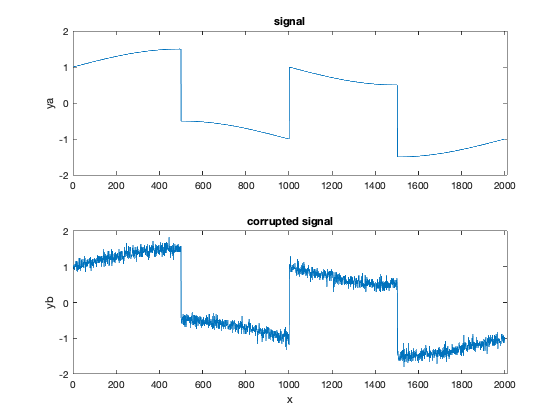
% 构建并画出原始信号
figure(1)
subplot(211)
temp = ones(ceil((n+1)/4),1);
exact= [temp; -temp; temp; -temp];
exact = exact(1:n+1) + 0.5*sin((2*pi/n)*t); 
plot(t,exact,'-');
axis([0 n+10 -2 2]);
ylabel('ya');
title('signal');
exact_variation = sum(abs(exact(2:(n+1)) - exact(1:n)))

% 构建并画出含噪的观测信号
subplot(212)
noise = 0.1*randn(size(t));
corrupt = exact+noise;
plot(t,corrupt,'-');
axis([0 n+10 -2 2]);
noisy_variation = sum(abs(corrupt(2:(n+1)) - corrupt(1:n)))
ylabel('yb');
xlabel('x');
title('corrupted signal');
%print -deps tv_exact_corrupt.eps % figure 6.11, page 315

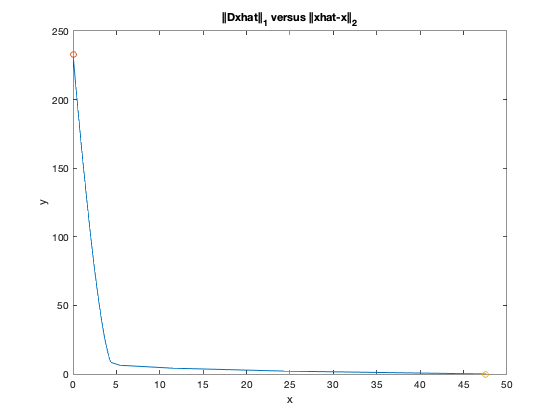
% 计算并画出全变差(total variation) vs ||x-xcorr||_2 的折中曲线
% figure 6.13 page 316
fprintf('computing 100 points on tradeoff curve ... \n');
nopts = 100;
TVs = linspace(0.01,.9*noisy_variation,nopts);

   obj1 = [];  obj2 = [];
   for i=1:nopts
     fprintf('tradeoff point %d\n',i);
     cvx_begin quiet
        variable xrec(n+1)
        minimize(norm(xrec-corrupt))
        subject to
            norm(xrec(2:(n+1))-xrec(1:n),1) <= TVs(i);
     cvx_end
     obj1 = [obj1, TVs(i)];
     obj2 = [obj2, norm(full(xrec-corrupt))];
   end;
   obj1 = [0 obj1 noisy_variation];
   obj2 = [norm(corrupt) obj2 0];

figure(2)
   plot(obj2,obj1,'-'); hold on
   plot(0,noisy_variation,'o');
   plot(norm(corrupt),0,'o');  hold off
   xlabel('x');
   ylabel('y');
   title('||Dxhat||_1 versus ||xhat-x||_2');
   %print -deps tv_tradeoff.eps % figure 6.13, page 316

figure(3)
   subplot(311)
   % 求解全变差问题
   cvx_begin quiet
    variable xrec(n+1)
    minimize(norm(xrec-corrupt))
    subject to
        norm(xrec(2:(n+1))-xrec(1:n),1) <= 10;
   cvx_end
   plot(t,xrec','-');
   axis([0 n -2 2]);
   ylabel('ya');
   title('xhat with TV=10');

   subplot(312)
   cvx_begin quiet
    variable xrec(n+1)
    minimize(norm(xrec-corrupt))
    subject to
        norm(xrec(2:(n+1))-xrec(1:n),1) <= 8;
   cvx_end
   plot(t,xrec','-');
   axis([0 n -2 2]);
   ylabel('yb');
   title('xhat with TV=8');

   subplot(313)
   cvx_begin quiet
    variable xrec(n+1)
    minimize(norm(xrec-corrupt))
    subject to
        norm(xrec(2:(n+1))-xrec(1:n),1) <= 5;
   cvx_end
   plot(t,xrec','-');
   axis([0 n -2 2]);
   xlabel('x');
   ylabel('yc');
   title('xhat with TV=5');

   %print -deps tv_rec_10_8_5.eps % figure 6.14, page 317

% 二次平滑, figure 6.12, page 316
% 这种情况下，没有必要使用CVX，因为存在解析解。
A = sparse(n,n+1); % n*(n+1)的零矩阵的稀疏形式
A(:,1:n) = -speye(n,n);  A(:,2:n+1) = A(:,2:n+1)+speye(n,n);

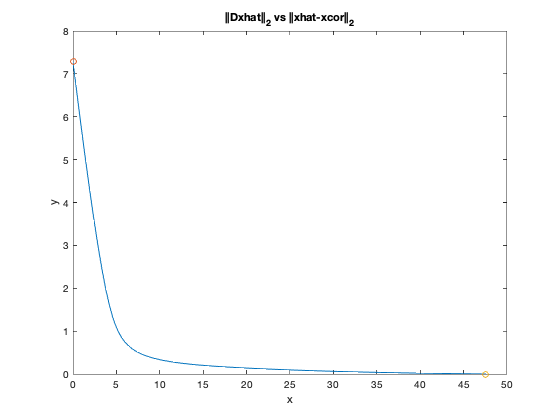
% 二次平滑的折中曲线
nopts = 100;
lambdas = logspace(-10,10,nopts);
obj1 = [];  obj2 = [];
for i=1:nopts

  lambda = lambdas(i);
  x = (A'*A+lambda*speye(n+1,n+1)) \ (lambda*corrupt);
  obj1 = [obj1, norm(full(A*x))];
  obj2 = [obj2, norm(full(x-corrupt))];
end;

figure(4)
plot(obj2,obj1,'-'); hold on
plot(0,norm(A*corrupt),'o');
plot(norm(corrupt),0,'o'); hold off
xlabel('x');
ylabel('y');
title('||Dxhat||_2 vs ||xhat-xcor||_2');
%print -deps tv_smooth_tradeoff.eps

nopts = 3;
alphas = [10 7 4];
xrecon = [];

for i=1:3
   alpha = alphas(i);
   u = 10;  l = -10;  normx = Inf;
   while (abs(normx-alpha) > 1e-3)
      lambda = 10^((u+l)/2);
      x = (A'*A+lambda*speye(n+1,n+1)) \ (lambda*corrupt);
      normx = norm(x-corrupt);
      if (normx > alpha), l = (u+l)/2; else u = (u+l)/2;  end;
   end;
   xrecon = [xrecon, x];

end;

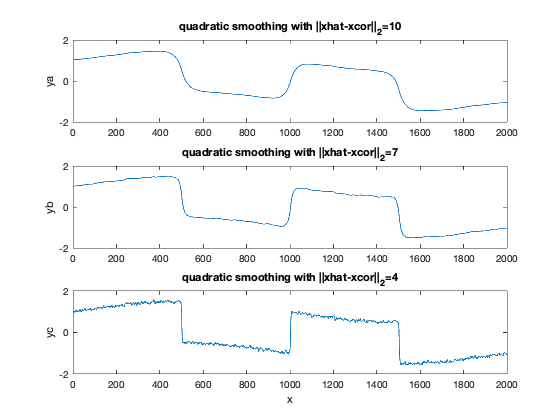
figure(5)
subplot(311), plot(xrecon(:,1));
axis([0 n -2 2])
ylabel('ya');
title('quadratic smoothing with ||xhat-xcor||_2=10');
subplot(312), plot(xrecon(:,2));
axis([0 n -2 2])
ylabel('yb');
title('quadratic smoothing with ||xhat-xcor||_2=7');
subplot(313), plot(xrecon(:,3));
axis([0 n -2 2])
xlabel('x');
ylabel('yc');
title('quadratic smoothing with ||xhat-xcor||_2=4');
%print -deps tv_smooth_tradeoff_examples.eps
% figure 6.12, page 316