参考自John Hedengren的一门课,网址是apmonitor.com
考虑这样一个反应:
![]()
要求画出物质A和B的浓度时间曲线。其中A的反应速率如下:
![]()
k=2.0,B的反应速率为 :
![]()
代码:
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
def rxt(C,t):
Ca=C[0]
Cb=C[1]
k=2.0
dAdt = -k*Ca
dBdt = k*Ca
return [dAdt,dBdt]
t=np.linspace(0,5,100)
C0=[1,0]
C=odeint(rxt,C0,t)
plt.plot(t,C[:,0],'r--',linewidth=2.0)
plt.plot(t,C[:,1],'b-',linewidth=2.0)
plt.xlabel('Time (s)')
plt.ylabel('Concentration')
plt.legend(['Ca','Cb'])
plt.show()
结果:?

?考虑反应2:
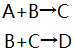
?A,B,C,D代表不同物质的浓度,单位 ,mol/L 。它们的初值分为:A0=1,B0=1,C0=0,D0=0
k1=1 L/mol*s,k2=1.5L/mol*s。定义反应活性S=C/(C+D),求ABCD和S的浓度-时间曲线
列微分方程组:

?代码:
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
def rxt(Z,t):
k1=1.0
k2=1.5
r1 = k1 * Z[0] * Z[1]
r2 = k2 * Z[1] * Z[2]
dAdt = -r1
dBdt = -r1 - r2
dCdt = r1-r2
dDdt = r2
return [dAdt, dBdt, dCdt, dDdt]
t=np.arange(0,3.01,0.2)
Z0=[1,1,0,0]
Conc = odeint(rxt,Z0,t)
cA=Conc[:,0]
cB=Conc[:,1]
cC=Conc[:,2]
cD=Conc[:,3]
S=np.empty(len(cC))
for i in range(len(cC)):
if(abs(cC[i]+cD[i])>1e-10):
S[i] = cC[i] / (cC[i]+cD[i])
else:
S[i] = 1
plt.plot(t,cA,'r--')
plt.plot(t,cB,'o-')
plt.plot(t,cC,'b--')
plt.plot(t,cD,'y-')
plt.plot(t,S)
plt.xlabel('Time (s)')
plt.ylabel('Concentration')
plt.legend(['cA','cB','cC','cD','S'])
plt.show()
结果:
