[人工智能]【论文阅读】Attention-based Deep Multiple Instance Learning

题目：CCF A-Loss-Based Attention for Deep Multiple Instance Learning

International conference on machine learning

摘要

多实例学习 (MIL) 是监督学习的一种变体，其中将单个类标签分配给一袋实例。
在本文中，我们将 MIL 问题描述为学习包标签的伯努利分布，其中包标签概率由神经网络完全参数化。此外，我们提出了一种基于神经网络的置换不变聚合算子，它对应于注意机制。值得注意的是，所提出的基于注意力的算子的应用可以深入了解每个实例对包标签的贡献。
我们凭经验表明，我们的方法在基准 MIL 数据集上实现了与最佳 MIL 方法相当的性能，并且它在基于 MNIST 的 MIL 数据集和两个真实组织病理学数据集上优于其他方法，而不会牺牲可解释性。

引入

多示例学习：
假设图像清楚地代表了一个类别（一个类）。然而，在许多实际应用中，会观察到多个实例，例如，计算病理学、乳房 X 线摄影或 CT 肺筛查）中尤为明显，其中图像通常由单个标签（良性/恶性）或区域描述粗略地给出了兴趣

MIL 处理分配了单个类标签的实例包。因此，MIL 的主要目标是学习一个预测袋子标签的模型
利用包之间的相似性 (Cheplygina et al., 2015b)，将实例嵌入到紧凑的低维表示中，然后进一步馈送到包级分类器、实例级分类器的响应

本文：
我们使用包标签的伯努利分布来制定 MIL 模型，并通过优化对数似然函数来训练它。

相关概念

置换不变（permutation-invariant）
对数似然函数（log-likelihood function）
伯努利分布（Bernoulli distribution）
对称函数（Symmetric Functions）
最大算子（maximum operator）
神经网络参数化
MIL 池化 σ
MIL 池化算子
最大算子
平均算子
tanh函数链接

方法

2.1. Multiple instance learning (MIL)

通过优化对数似然函数来训练 MIL 模型，其中袋标签根据伯努利分布分布，即给定实例包 X，Y = 1 的概率

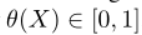
Theorem 1 包$\mathbf{X}$的评分函数，其中 f 和 g 是合适的变换。给出的分解对袋子概率建模的一般策略。

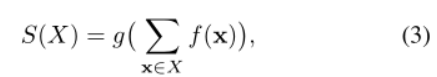
Theorem 2 用 max 而不是 sum 的类似分解

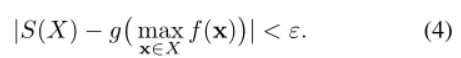
共同点：一种通用的三步方法来对包进行分类：（1）用函数 f 对实例进行转换（2）使用对称（排列不变）函数σ对转换后的实例进行组合（3）由f使用函数g变换的组合实例的变换

于给定的 MIL 运算符，有两种主要的 MIL 方法：（1）实例级方法 （2）嵌入级方法
我们将展示如何通过使用新的 MIL 池来修改嵌入级方法以使其可解释。

2.2. MIL with Neural Networks

由神经网络 fψ(·) 参数化的变换；$h_k\in \mathcal{H}$;若$h_k\in 0,1$,则为基于实例的方法；若$h_k\in {\mathbb{R}}^M$,则为嵌入的方法

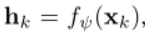
转换$g_{?}$:在基于实例的方法中，变换 gφ 只是恒等式，而在基于嵌入的方法中，它也可以由具有参数 φ 的神经网络参数化

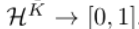
2.3. MIL pooling

两个MIL池化算子保证得分函数为对称函数：
（1）最大算子

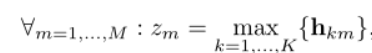
(2)平均算子

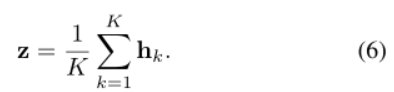
（3）其他算子代替定理2中的max
例如凸最大算子（即 log-sum-exp）、集成分割和识别、噪声或和噪声和

2.4. Attention-based MIL pooling

所有 MIL 池化算子都有一个明显的缺点，即它们是预定义的且不可训练的。因此，灵活和自适应的 MIL 池可以通过调整任务和数据来获得更好的结果。
使用实例的加权平均值（低维嵌入），其中权重由神经网络确定。其中权重与嵌入一起是 f 函数的一部分

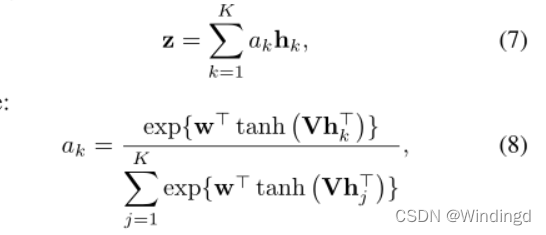
我们注意到 tanh(·) 非线性对于学习复杂关系可能效率低下，因此，我们建议额外使用门控机制 以及 tanh(·) 非线性：