[人工智能]神经网络1.1 感知机模型(神经元模型)

1.激活函数

1.1 Sigmoid函数

Sigmoid 是常用的非线性的激活函数，表达式如下：
$$f(x)=\frac{1}{1+e^{?x}}$$

• 特性：它能够把输入的连续实值变换为$0$和$1$之间的输出，特别的，如果是非常大的负数，那么输出就是$0$；如果是非常大的正数，输出就是$1$.
• 缺点：在深度神经网络中梯度反向传递时导致梯度爆炸和梯度消失，其中梯度爆炸发生的概率非常小，而梯度消失发生的概率比较大。

1.2 tanh函数

tanh函数也是非线性函数，其函数解析式为：
$$tanh(x)=\frac{e^x?e^{?x}}{e^x+e^{?x}}$$
tanh读作Hyperbolic Tangent，它解决了Sigmoid函数的不是zero-centered输出问题，然而，梯度消失(gradient vanishing)的问题和幂运算的问题仍然存在。

1.3 Relu函数

Relu函数实际上就是个取最大值函数，其函数解析式如下所示：
$$f(x)=\max (0,x)$$

• Relu是目前最常用的激活函数，一般搭建人工神经网络时推荐优先尝试
• Relu并非全区间可导，但我们可以取sub-gradient
• 1. 解决了gradient vanishing问题 (在正区间)
  2. 计算速度非常快，只需要判断输入是否大于$0$
  3. 收敛速度远快于Sigmoid和tanh
• 1. ReLU的输出不是zero-centered
  2. Dead ReLU Problem，指的是某些神经元可能永远不会被激活，导致相应的参数永远不能被更新。有两个主要原因可能导致这种情况产生: (1) 非常不幸的参数初始化，这种情况比较少见 (2) learning rate太高导致在训练过程中参数更新太大，不幸使网络进入这种状态。解决方法是可以采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。

1.4 Leaky ReLU函数(PReLU)

函数表达式：
$$f(x)=\max (\alpha x,x)$$
人们为了解决Dead ReLU Problem，提出了将ReLU的前半段设为$\alpha x$而非$0$，通常$\alpha =0.01$。另外一种直观的想法是基于参数的方法，即$ParametricReLU:f(x)=\max (\alpha x,x)$，其中$\alpha$
可由方向传播算法学出来。理论上来讲，Leaky ReLU有ReLU的所有优点，外加不会有Dead ReLU问题，但是在实际操作当中，并没有完全证明Leaky ReLU总是好于ReLU。

1.5 ELU(Exponential Linear Units) 函数

函数表达式：
$$f(x)=\{\begin{array}{cc}x,& ifx>0\\ \alpha (e^x?1),& otherwise\end{array}$$
ELU不会有Dead ReLU问题 输出的均值接近$0$，zero-centered。但计算量偏大，在目前的实际应用中并未被证明总是好于ReLU。

1.6 UnitStep 阶跃函数

函数表达式：
$$f(x)=\{\begin{array}{cc}1,& ifx>0\\ 0,& otherwise\end{array}$$
一般用于感知机的激活函数。但感知机用梯度下降法求解更优。

2.感知机模型(神经元模型)

设输入空间(特征空间)为$X?{\mathbb{R}}^n$，输出空间为 Y = { 0 , 1 } Y = \{0, 1\} Y={0,1}

输入$x\in X$为实例的特征向量，输出$y\in Y$为实例的类别

由输入空间到输出空间的如下函数称为感知机：
$$f(x)=sign(wx+b)$$
其中$w$和$b$为模型参数，$w\in {\mathbb{R}}^n$称为权值，$b\in \mathbb{R}$称为偏置。$sign$是符号函数。

假设我们目前的任务是通过感知机对具有$n$维特征的向量进行分类。我们可以将该感知机的模型视作一个神经元模型。$n$维向量($(x_1,x_2,\dots ,x_n)$)对应的是神经元的$n$个输入。

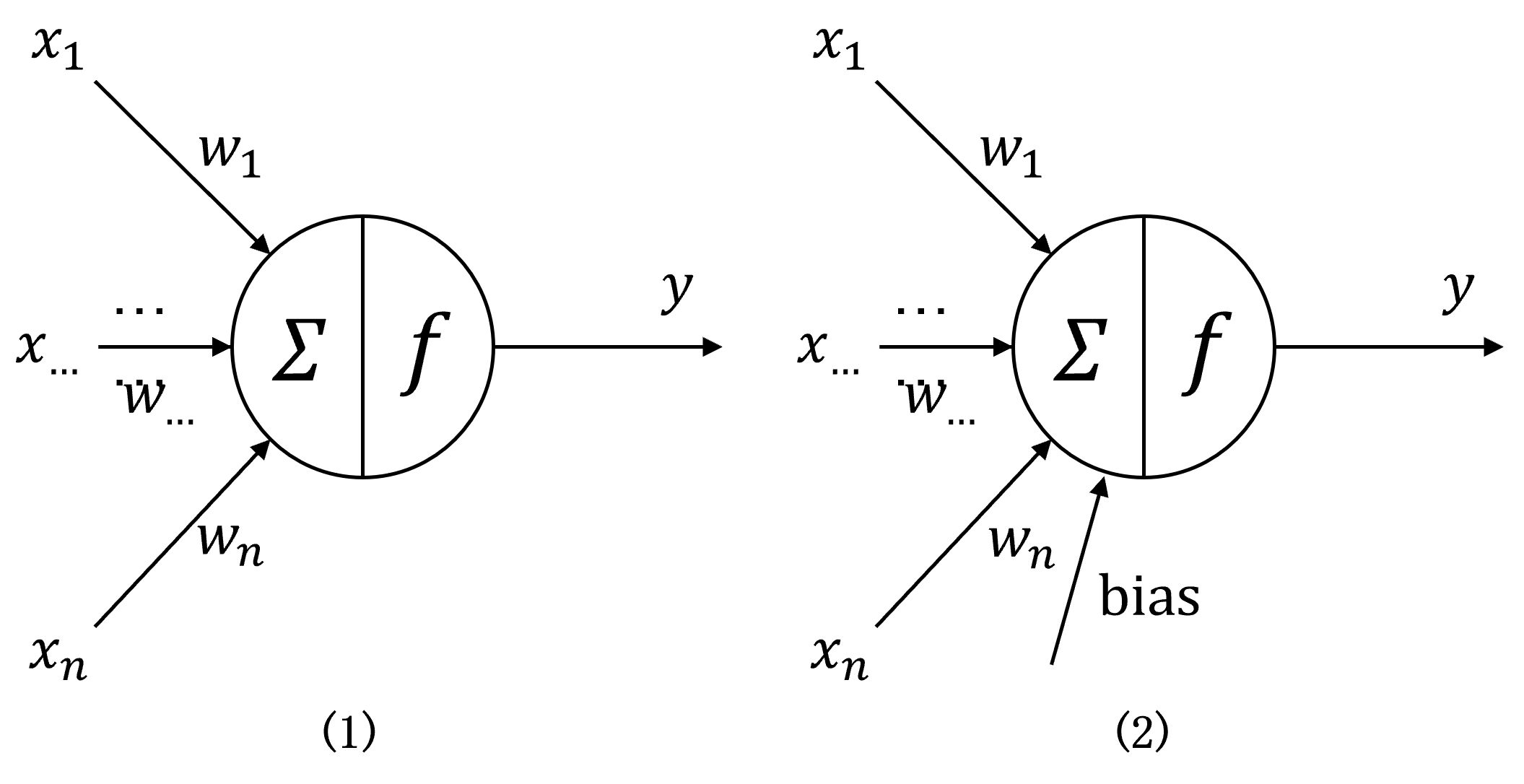
我们对这$n$个输入分别乘其对应的权值后求和，经过激活函数后得到分类结果。

但是我们注意到，当神经网络的输入向量为$0$时，会产生激活失败误分类的情况，为了避免这种情况，我们对其加偏置项后再进入激活函数，也就是感知机模型中的$b$。

我们首先对输入向量乘对应的权值加偏置项后得到${\sum }_{k=1}^{k\le n}w{x}_i+b$，将其经过激活函数后与标签进行比对，并根据是否与标签相等来更新参数的值：
$$\begin{gathered} w=w+\alpha \times (y?\hat{y})\times x \\ b=b+\alpha \times (y?\hat{y}) \end{gathered}$$
其中$\alpha$为步长，又称学习率。以上过程对所有训练数据执行一次后，可以得到一轮训练后的$w$和$b$。

显然，由于权值参数对应于$n$维特征向量，因此$w$的维度一定与输入向量的特征维数有关。

此处给出基于Python实现的感知机模型。

import numpy as np
import matplotlib.pyplot as plt 

class ActivateFunction(object):
    @staticmethod
    def Sigmoid(x):
        return (1 / (1 + np.exp(-x)))
    @staticmethod
    def ReLu(x):
        if x <= 0: return 0
        else: return x
        #return np.max(0, x)
    @staticmethod
    def Softmax(x):
        return np.exp(x) / np.sum(np.exp(x))
    @staticmethod
    def UnitStep(x):
        return 1 if x > 0 else 0
    

class Perceptron(object):
    #初始化一个具有n维特征的感知机
    def __init__(self, input_num, activator):
        self.activator = activator
        self.size = input_num
        self.weights = [0.0 for i in range(input_num)]
        self.bias = 0.0
	#预测值
    def Predict(self, input_vec):
        return self.activator(np.dot(input_vec, self.weights) + self.bias)
	#单轮训练
    def SingleIteration(self, input_vecs, labels, rate):
        samples = zip(input_vecs, labels)
        for (input_vec, label) in samples:
            output = self.Predict(input_vec)
            delta = label - output
            input_vec = np.array(input_vec)
            self.weights += rate * delta * input_vec
            self.bias += rate * delta
	#多轮训练入口
    def fit(self, input_vecs, labels, iteration, rate):
        input_vecs, labels = np.array(input_vecs), np.array(labels)
        for i in range(iteration):
            self.SingleIteration(input_vecs, labels, rate)
	#获取训练后的得到参数
    def GetParameters(self):
        return self.weights, self.bias


if __name__ == "__main__":
    data, label = [], []
    file = open(r'.\Python\x.txt')
    for line in file.readlines():
        line_data = line.strip().split(',')
        data.append([float(line_data[0]), float(line_data[1])])
    file.close()
    file = open(r'.\Python\y.txt')
    for line in file.readlines():
        line_data = line.strip().split(',')
        label = list(map(int, line_data))
    file.close

    p = Perceptron(2, ActivateFunction.UnitStep)
    p.fit(data, label, 1000, 0.1)
    w, b = p.GetParameters()
    x1 = np.arange(-5, 10, 0.1)
    x2 = (w[0] * x1 + b) / (-w[1])

    data = np.array(data)
    label = np.array(label)
    idx_p = np.where(label == 1)
    idx_n = np.where(label != 1)
    data_p = data[idx_p]
    data_n = data[idx_n]
        
    plt.scatter(data_p[:, 0], data_p[:, 1], color='red')
    plt.scatter(data_n[:, 0], data_n[:, 1], color='blue')
    plt.plot(x1, x2)
    plt.show()

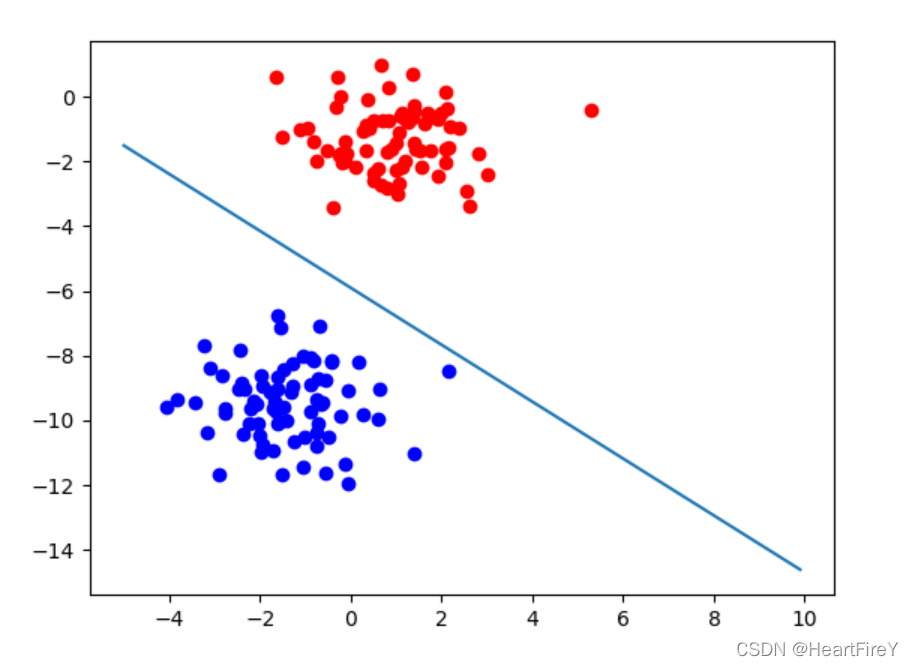
分类效果示例如上所示。