Multiclass Optimal Classification Trees with SVM-splits(2021)
支持向量机分裂的多类最优分类树
V Blanco,A Japón,J Puerto
文章目录
摘要:
在本文中,我们提出了一种新的基于数学优化的方法来构造多类实例的树形分类规则。我们的方法包括建立分类树,其中,除了叶节点,标签被暂时忽略,并通过SVM分离超平面将其分为两类。我们为这个问题提供了一个混合整数非线性规划公式,并报告了一系列扩展计算实验的结果,以评估我们的建议相对于其他基准分类方法的性能。
1.导言
解释性是机器学习方法的一个关键要求,在过去十年中出现了大量的方法[21]。除了能够充分预测样本外观察的行为外,还可以解释使用训练样本的机器学习方法时产生的模型。不同的工具已被用于衍生可解释的机器学习方法。简化得到的模型最常用的策略之一是特征选择,在这种策略中,在不降低预测质量的情况下选择一组简化的属性。通过减少要分析的参数数量,模型可以更容易理解,产生更高的描述精度。人们也可以考虑可以被调制的模型,从某种意义上说,它的预测过程的很大一部分可以独立地解释。这是广义线性模型的情况[29]。其他方法将可解释性作为人类在其整个结构中可以复制的同义词[15,34]。
决策树的深度很小,即使用户不熟悉其构造背后的工具,也可以很容易地对其进行可视化和解释。本文采用了基于树的方法。
在机器学习的视角下衍生出的各种链中,分类因其在许多不同领域的适用性而引起了广泛关注[4,28,31,36,41]。分类方法旨在充分预测新观测值的类别,前提是使用给定样本构建分类规则。数学规划在构建分类模型中的作用已得到广泛认可,一些最流行的推导分类规则的方法是基于解决优化问题[13,17,16,11,27]。此外,当需要对获得的模型进行解释时,数学规划也被证明是一种灵活而准确的工具[5,6,12,25]。
然而,大多数用于构造分类器的优化工具都假设实例只有两个类。在本文中,我们提供了一种新的分类方法,在这种方法中,实例可以被划分为两个或多个类别。该方法使用最具解释性的分类方法之一分类树构建,但与支持向量机相结合,后者提供了高度预测的模型。
我们开发了一个数学规划模型,可以为给定的训练样本构建一个最优分类树,其中每个分类都是通过基于SVM的超平面生成的。在构建树时,在分支节点中忽略观测值的标签,并且只在考虑误分类错误的叶节点中考虑这些标签。构建分类树是为了最小化树的复杂性(确保可解释性)和误分类风险(确保预测能力)。
1.1相关工作
为了构建高度预测??的分类规则,文献中已经提出了几种机器学习方法。最流行的是基于深度学习机制 [1]、k-最近邻域 [18、42]、朴素贝叶斯 [35]、分类树 (CT) [15、23] 和支持向量机 (SVM) [17] .其中,CT 和 SVM 本质上是基于优化的方法,除了产生高度预测的分类器外,已被证明是非常灵活的工具,因为它们都允许结合不同的元素(通过适当的优化模型通过约束和目标函数)以适应不同的情况,如特征选择 [27, 5, 6, 30],准确性要求 [7, 24] 或处理不平衡或嘈杂的实例 [22, 10, 14] 等。
支持向量机最初是由 Cortes 和 Vapnik [17] 作为一种二元分类工具引入的,它通过在两个类之间具有较大间隔的分离超平面来构建决策规则。这个超平面是通过求解一个凸二次优化问题得到的,其目标是通过两个不同的类来分离数据,最大化它们之间的边距并最小化错误分类错误。该优化问题的对偶特性允许扩展方法以通过内核来找到非线性分离器。分类树首先由 Breiman 等人介绍。 al [15],并且决策规则基于一组节点之间的层次关系,该层次关系用于定义将观察结果从根节点(层次关系中的最高节点)引导到某些叶子的路径,其中类被分配给数据。这些路径是根据对训练样本的预测变量的不同优化标准获得的。决策规则自然而然地出现,为新观测预测的类是分配给观测所在的终端节点的类。显然,从 CT 派生的分类规则很容易通过在树节点处构造的拆分来解释.在 [15] 中,提出了一种贪婪的启发式程序,即所谓的 CART 方法来构建 CT。树的每一层是按顺序构造的:从根节点开始,使用整个训练样本,该方法最小化杂质测量函数,作为结果,将样本分成两个不相交的集合,确定两个后代节点。重复此过程,直到达到给定的终止标准(属于叶的最小观察数、树的最大深度或叶上同一类的最小观察百分比等)。在这种方法中,树按照自上而下的贪心方法生长,这一想法在 C4.5 [40] 或 ID3 [39] 等其他流行的决策树方法中也有共享。这些方法的优点是即使对于大型训练样本也可以相当快地获得决策规则,因为整个过程依赖于解决每个节点的可管理问题。然而,这些类型的启发式方法可能无法获得最佳分类树,因为它们在每个节点本地寻找最佳分割,而不考虑随后的分割。因此,这些本地分支可能无法捕获数据的正确结构,从而导致样本外观察中的错误分类错误。此外,这些方法提供的解决方案可能会导致非常深(复杂)的树,导致过度拟合,有时会失去分类规则的可解释性。这个困难通常通过修剪树来克服,因为它是通过比较杂质测量减少的增益与树的复杂性成本来构建的。
最近在建模和解决困难的优化问题方面取得的进展,以及这些模型的灵活性和适应性,促使人们使用优化工具来构建监督分类方法,并取得了巨大成功[9,16])。尤其是最近,Bertsimas和Dunn[8]提出了在最优化镜头下逼近分类回归树的最优分类树(OCT)的概念,给出了最优构造的混合整数线性规划公式。此外,作者还证明了该模型对于合理大小的数据集是可以求解的,同样重要的是,对于许多不同的真实数据集,相对于CART,该模型的精度可以得到显著的提高。与标准CART方法不同,OCT通过解决单个优化问题(在目标函数中)考虑树的复杂性来构建树,避免了后期修剪过程。此外,每次分割都是直接应用的,以便最大限度地减少终端节点上的错误分类错误,因此OCT更有可能捕获数据的隐藏模式。
虽然 SVM 最初设计为仅处理二类实例,但文献中已经提出了一些扩展用于多类分类。最流行的基于多类 SVM 的方法是 One-Versus-All (OVA) 和 One-Versus-One (OVO)。前者,即 OVA,计算每个类 r ∈ {1, . . . , k},一个二元 SVM 分类器,如果观测值属于 r 类,则将观测值标记为 1,否则为 -1。对所有类重复该过程(k 次),然后将每个观察分类到其构造的超平面在正半空间中离它最远的类。在 OVO 方法中,每对类使用一个超平面将类与 k/2 个超平面分开,并且决策规则来自投票策略,其中投票中代表最多的类成为预测的类。
OV A 和 OVO 继承了二进制 SVM 的大部分优良特性。尽管如此,当使用线性核时,他们无法正确分类数据集,其中分离的观察云可能属于同一类(因此被赋予相同的标签)。另一种流行的方法是有向无环图 SVM,DAGSVM [1]。在这种技术中,尽管决策规则涉及使用 OVO 方法构建的相同超平面,但它不是由唯一的投票策略给出的,而是针对连续数量的投票,其中最不可能的类被删除,直到只剩下一个类。此外,除了 OV A 和 OVO,还有一些基于将原始多类问题分解为多个二分类问题的方法。特别是,在 [2] 和 [20] 中,这种分解是基于编码矩阵的构建,该矩阵确定将用于构建分离超平面的类对。或者,其他方法,如 CS ([19])、WW ([44]) 或 LLW ([33]),不是按顺序解决分类问题,而是作为一个整体考虑同一优化模型中的所有类。显然,这似乎是正确的做法。特别是,在 WW 中,k 个超平面用于分离 k 个类别,每个超平面将一个类别与其他类别分开,每个观察使用 k-1 个错误分类错误。
在 CS 中应用了相同的分离思想,但将每个观察的错误分类错误的数量减少到一个唯一值。在 LLW 中,提出了一种不同的误差度量来将贝叶斯分类规则转换为 SVM 问题,这意味着所获得的分类器中的理论统计特性。在 WW 或 CS 中无法确保这些属性
我们还可以找到基于 [26] 提出的 LLW 的二次扩展。在 [43] 中,作者提出了一种基于多类 SVM 的方法 GenSVM,其中使用单纯形编码在 (k-1) 维空间中获得 k 类问题的分类边界。其中一些方法已经变得流行,并在机器学习中的大多数软件包中实现,如 e1071 [37]、scikit-learn [38] 或 [32]。最后,在最近的工作 [11] 中,作者提出了一种处理多类分类的替代方法,该方法扩展了二元 SVM 分类器的范式,通过构造特征空间的多面体分区并将类分配给分区的单元格,通过最大化类之间的分离并最小化两个直观的错误分类错误。
1.2贡献
在本文中,我们提出了一种通过数学规划模型为多类实例构建分类树的新方法。我们的方法基于两个主要成分:
(1)在 [8] 的意义上构建了一个最优二叉分类树(带有斜切),其中分裂和修剪节点是根据叶处的错误分类错误来确定的节点;
(2) 生成树分支的分裂是通过基于二元支持向量机的超平面分离虚构类(这也由模型决定)构建的,即最大化类之间的分离并最小化基于距离的错误分类错误。
我们的具体贡献包括:
(1)导出一个可解释的多类分类规则,它结合了监督分类中两个最强大的工具,即 OCT 和 SVM。
(2)分类器是使用可以表述为混合整数二阶锥规划问题的数学规划模型构建的。该分类器易于应用和解释。
(3)为公式提出了几个有效的不等式,它们允许加强模型并在更短的 CPU 时间内解决更大尺寸的实例。
(4)据报道,对来自 UCI 的真实数据进行的大量计算实验表明,我们的方法优于其他基于决策树的方法,如 CART、OCT 和 OCT-H。
1.3 论文结构
第2节将修复符号,并回顾用于派生我们的方法的工具。在第3节中,我们详细介绍了我们的方法的主要成分,并通过一个示例演示了它的性能。第4节给出了允许我们构建分类器的数学规划模型,其中包括模型中涉及的所有元素:参数、变量、目标函数和约束。在第5节中,我们报告了实验的结果,以评估与其他树形分类器相比,我们的方法的性能。最后,第6节给出了一些结论和未来的研究方向。
2. 预处理
本节专门介绍所研究的问题并修正本文使用的符号。我们还回顾了我们提出的方法中涉及的主要工具,即支持向量机和最优分类树。这些方法充分结合以开发一种新方法,称为基于支持向量机的拆分的多类最优分类树 (MOCTSVM)。
我们得到一个训练样本,X = {(x1, y1), . . . , (xn, yn)} ? Rp×{1, . . . , K},这是在一组 n 个观测值 (x1, . . . , xn) 上测量 p 个特征以及 {1, . . . , K} 为它们中的每一个 (y1, . . . . , yn)。分类方法的目标是建立决策规则,以便根据给定训练样本 X 的行为准确地将标签 (y) 分配给数据 (x)。
我们在方法中使用的第一个成分是支持向量机方法。 SVM 是最流行的基于优化的方法之一,用于设计只涉及两个类的分类规则,通常称为正类 (y = +1) 和负类 (y = -1)。线性支持向量机的目标是通过最大化它们的分离并同时最小化错误分类和边际违规错误来构造一个分离这两个类的超平面。线性 SVM 可以表述为以下凸优化问题:
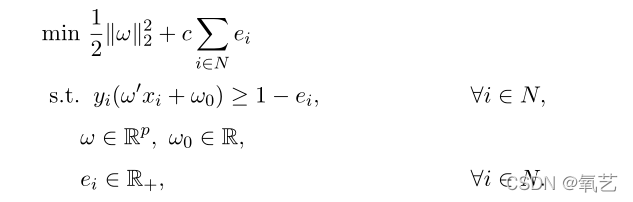
其中 c 是正则化参数,表示训练误差和模型复杂度(边距)之间的权衡,ω’ 是向量 ω 和 ||.|| 的转置。是 Rp 中的欧几里得范数(也可以考虑其他范数,但仍保持优化问题 [13] 的相似结构特性)。请注意,使用这种方法,正(或负)类将倾向于位于由超平面 H = {z ∈ Rp : ω’z +ω0 = 0} 诱导的正(或负)半空间上。另一方面,SVM 的流行主要是由于所谓的内核技巧。这允许人们将数据投影到更高维空间,在其中以最准确的方式执行线性分离,无需知道这样的空间,而只需知道其内积的形式,并保持计算复杂度优化问题(更多细节参见[17])。
我们在方法中结合的第二种方法是分类树。 CT 是一系列基于一组节点之间的层次关系的分类方法。这些方法允许人们通过按顺序构建的超平面来创建特征空间的分区。 CT 从包含整个样本的节点开始,即称为根节点,其中应用了第一个拆分。当在节点上应用拆分时(通过超平面分离观察值,会创建两个新分支,导致两个新节点,称为其子节点。节点通常分为两组:分支节点,即是应用分裂的节点,另一方面是叶节点,它们是树的终端节点。给定一个分支节点和在这样一个节点中分裂的超平面,它们的分支(左和右)定义为由超平面定义的两个半空间中的每一个。CT 的最终目标是构造分支,以获得关于类的叶节点尽可能纯。这样,给定观察的分类规则包括分配它到它所属的叶子中最受欢迎的类。
有大量关于 CT 的文献,因为它们提供了易于解释的分类规则。构建 CT 的最流行方法之一称为 CART,在 [15] 中进行了介绍。 CART 是一种贪婪的启发式方法,它从根节点开始寻找单个特征中的拆分,以最小化给定的杂质函数,创建两个新节点。依次应用相同的过程,直到达到停止标准(树的最大深度、节点中单个类的观察比例等)。 CART 的主要优点是计算成本低,因为现在可以在几秒钟内获得非常深的树。然而,CART 并不能保证分类树的最优性,从某种意义上说,如果不是局部构建分支,而是查看叶节点的最终配置,则可以获得更准确的树。例如,在图 1(左)中,我们展示了 CART 为最大深度为 2 的二分类问题构建的 CT。我们绘制分类树,并在右上角绘制特征空间的分区(在本例中为 R2 )。
可以看出,获得的分类并不完美(并非所有叶节点都由纯类组成),而在这种情况下构造一个没有分类错误的 CT 并不困难。这种情况是由 CART 方法所做的短视构造引起的,即在每个节点只关心其子节点的更好分类,而不关心最终叶节点的分类,而随后的分支决策显然会影响树的整体形状。
受 CART 的这一缺点的启发,在 [8] 中,作者提出了一种通过解决单个数学规划问题来构建最优分类树 (OCT) 的方法,在该问题中,不仅可以进行单变量拆分,还可以进行涉及多个变量的倾斜拆分。可以构建预测变量(通过特征空间中的一般超平面)。在图 1(右)中,我们展示了 OCT 为同一示例提供的具有超平面 (OCT-H) 的解决方案。可以观察到,在拆分根节点(橙色分支)时,没有获得良好的局部拆分(节点包含不同类别中的一半观察值),但是,当添加其他两个拆分时,最终的叶子只有对同一类,从而为训练样本产生完美的分类规则。
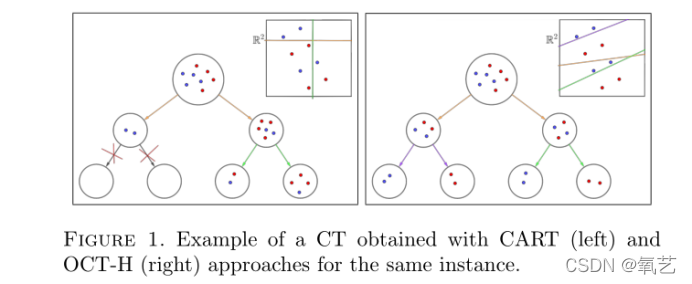
图 1. 使用 CART(左)和 OCT-H(右)方法为同一实例获得的 CT 示例。
在 SVM 方法的意义上,OCT 和 SVM 两种方法可以结合起来,以构建分类树,其中由 CT 中确定的超平面分隔的类最大程度地分离。这个想法并不新鲜,并且已被证明在许多不同的二分类问题中优于标准的最优决策树方法,例如,在 [12] 中提出了 OCTSVM 方法。在图 2 中,我们展示了如何使用 OCTSVM 构建具有更大类别间隔的 OCT,但在训练样本中仍具有与 OCT-H 相同的 100% 准确度,但在样本外观察中更能防止错误分类。
然而,据我们所知,OCT 和 SVM 的组合只针对二类实例进行了分析。将此方法扩展到多类设置(多于两个类)并非易事,因为可以构建更复杂的树或使用基于多类 SVM 的方法(参见例如 [19,44,33])。
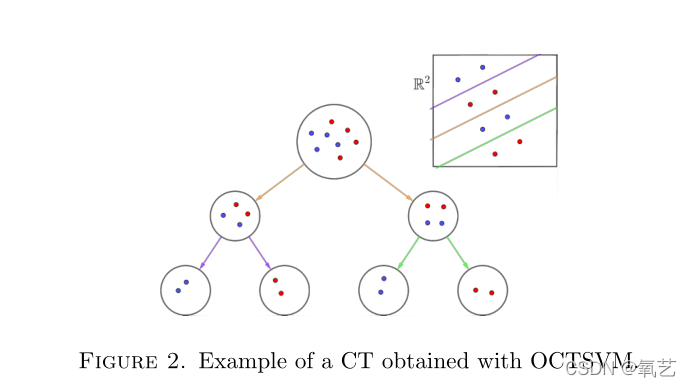
图 2. 使用 OCTSVM 获得的 CT 示例。
然而,经典 SVM 方法的这些改编已被证明在现实世界的实例中失败(参见 [11])。在本文的其余部分中,我们描述了一种基于不同思想构建精确的多类树形分类器的新方法:构造具有由双类 SVM 分离器引起的分裂的 CT,其中每个分支节点处的观察类由模型确定,但经过充分选择以在叶节点处提供小的分类误差。该方法的详细信息将在下一节中给出。
3.带 SVM 拆分的多类 OCT
在本节中,我们描述了我们建议为多类实例构建分类规则的方法,特别是基于 SVM 范式生成拆分的分类树。如前所述,我们的方法基于使用 SVM 拆分构造 OCT,但观察的类别暂时被忽略,仅在叶节点处考虑。为了说明我们方法下的想法,在图 3 中,我们展示了一个玩具实例,其中包含一组具有四种不同类别(蓝色、红色、橙色和绿色)的点。

图 3. 4 类问题的实例
首先,在根节点(涉及所有观察的节点),我们的方法为两个虚构类(也必须确定)构造一个 SVM 分离超平面。一种可能的分离可能是图 4 中所示的分离,其中训练数据集已分为两类(黑色和白色)。这种分离允许生成两个子节点,即黑色和白色节点。在每个节点上,应用相同的想法,直到到达叶节点。在图 5 中,我们根据此过程显示了特征空间的最终划分。

图 4. 4 类分类问题的根分裂

图 5. 4 类分类问题上的子节点分裂,在我们的模型中确定为虚构类。
显然,在整个过程中忽略训练样本的原始类别将导致无意义的树,除非在叶节点处考虑到训练样本中分类规则的优点。因此,在最终的叶节点处,原始标签被恢复,并根据生成的超平面进行分类。这棵树的最终结果如图 6 所示,其中可以检查构建的树是否实现了对训练样本的完美分类。
一旦使用这种策略构建树,决策规则就会自然而然地出现,就像在决策树方法中通常所做的那样,即样本外的观测值将根据拆分遵循树上的路径,并将它们分配给他们所在的叶子的类(训练集上最具代表性的叶子类)。如果在构建树时修剪了一个分支,则观察将分配给发生修剪的节点的最具代表性的类。

图 6. 带有原始标签(颜色)的 4 类分类问题的子节点分裂。
4.MOCTSVM 的数学规划公式
在本节中,我们为上一节中描述的 MOCTSVM 方法推导出混合整数非线性规划公式。我们假设给定一个训练样本 X = {(x1, y1), . . . , (xn, yn)} ? Rp × {1, . . . , ?}。我们用 N = {1, . . . , n} 训练样本中观测值的索引集。我们还将标签 y 的二进制表示视为:
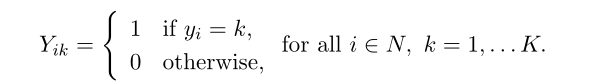
此外,在不失一般性的情况下,我们将假设要归一化的特征,即 x1, 。 . . , xn ∈ [0, 1]p。
我们将构建具有固定最大深度 D 的决策树。因此,分类树最多由 T = 2D+1 - 1 个节点组成。我们用 τ = {1, . . . , T } 为树节点设置的索引,其中节点 1 是根节点,节点 2D,. . . , 2D+1 - 1 是叶节点。
对于任何节点 t ∈ τ{1},我们用 p(t) 表示它的(唯一的)父节点。树节点可以分为两组:分支节点和叶节点。我们用 Tb 表示的分支节点将是应用拆分的节点。相反,在由 T1 表示的叶节点中,没有应用分裂,而是发生预测的地方。分支节点也可以分为两组:Tbl 和 Tbr,这取决于它们分别从其父节点沿路径上的左分支还是右分支。 τbl 节点用偶数索引,同时 τbr 节点用奇数索引。
我们将级别定义为在树中具有相同深度的一组节点。由于根节点被假定为零级,因此要构建的树中的级别数为 D + 1。令 U = {u0, . . . , uD} 是树的层集,其中每个 us ∈ U 是层 s 的节点集,对于 s = 0, . . . , D. 使用这种表示法,根节点是 u0 而 uD 表示叶节点的集合。
图七中,我们在3深度树中显示了上述元素。
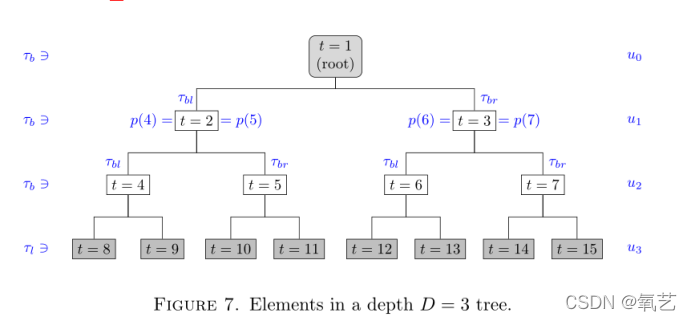
图 7. 深度 D = 3 树中的元素
除了关于树的拓扑结构的信息外,我们还考虑了三个必须在验证过程中校准的正则化参数,它们使我们能够在模型中结合的不同目标之间找到权衡:边际违规和分离分裂超平面的分类误差、叶节点的正确分类和树的复杂度。这些参数如下:
c1:叶节点的单位错误分类成本。
c2:基于单位距离的 SVM 拆分错误分类错误。
c3:树中引入的每个分裂超平面的单位成本。
表 1 总结了我们模型中使用的索引集和参数的完整列表。
4.1变量
我们的模型使用表 2 中描述的一组决策和辅助变量。我们使用二元和连续决策变量来模拟 MOCTSVM。二元变量允许我们决定将观察结果分配给决策树节点,或者决定一个节点是否在树中被分割。连续变量允许我们确定分裂超平面的系数或错误分类错误(在 SVM 分离中或在叶节点处)。我们还使用有助于充分建模问题的辅助二进制和整数变量。
在图 8 中,我们说明了这些变量在具有三个类别(红色、蓝色和绿色)的玩具实例的可行解决方案中的使用。


在根节点(节点 t = 1)处考虑整组训练观察。在那里,原始标签被忽略,并且为了确定每个观察的虚构类,构建了一个基于 SVM 的超平面。
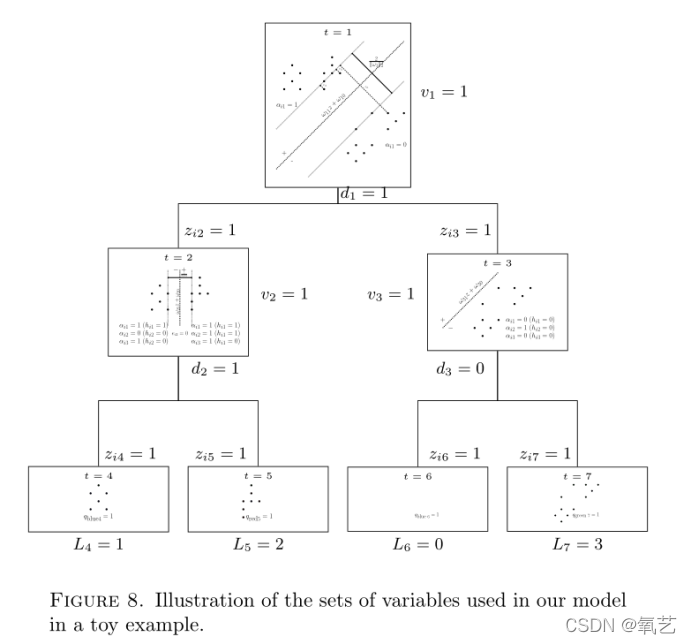
这样的超平面由系数 ω1 ∈ Rp 和 ω10 ∈ R 定义(超平面/图中用虚线绘制的线),它会导致边缘分离(2/||w1||2)和错误分类错误 ei1。在图中绘制的可行解中,只有三个观测值会导致正误差(那些被分类在边缘区域或超平面对面的误差)。这样的超平面也决定了该节点的子节点定义的分裂规则。由于节点是分裂的(d1 = 1),属于超平面正侧的观察被分配给左节点(节点 t = 2),而负侧的观察被分配给右节点(节点 t = 3) 通过 z 变量。
在节点 t = 2,应用相同的方案,即构建由 ω2 定义的超平面,引入基于 SVM 的余量和误差,并且由于 d2 = 1,分割规则也适用于定义节点 t = 4 和 t = 5. 在节点 t = 2 处,必须控制该节点中的观察,以量化仅针对目标函数中的那些观察的误分类误差 ei2。具体来说,我们只考虑属于节点 (zi2 = 1) 并且属于超平面的正侧 (αi2 = 1) 或负侧 (αi2 = 0) 的观测值的这些误差。此外,为了控制树的复杂性,使用 h 变量来了解观察是否属于节点和 SVM 超平面的正侧。
如果一个节点中的所有观测值都属于超平面的正侧,则变量 v 取值为 0。否则,如果 v 取值为 1,则可能出现两种情况:1)在超平面的两侧都有观测值(如在节点 t = 2) 中诱导新的分裂 (d2 = 1),以及 2) 所有观察都属于负侧(如在节点 t = 3 中),确定树在该节点处被修剪(d3 = 0)。
关于叶子节点,节点 t = 2 被分裂为节点 t = 4 和 t = 5,并且决定不再分裂的节点 t = 3 被虚拟分裂为两个叶子节点,尽管其中一个是空的并且另一个接收父节点(节点 t = 3)的所有观察结果。将任何叶节点 τl 分配给一个类是通过 q 变量完成的(分配给节点中最流行的类,或者在节点没有观测值的情况下任意分配),并且错误分类的观测值的数量由 L 变量解释.
4.2 目标函数
如前所述,我们的方法旨在构建在叶节点处具有小错误分类误差的分类树,但同时具有基于 SVM 的超平面和基于距离的最小误差的类之间的最大分离。使用上一节中描述的变量,目标函数中包含的四个项如下:

分裂超平面的边距:: 分支节点 t ∈ Tb 的分离超平面的边距为 2/||wt||2。因此,我们的方法旨在最大化这些边距的最小值。这相当于最小化由辅助变量 δ 表示的逆边际 { 1 2kωtk22 : t ∈ τb} 中的最大值。叶节点处的误分类错误::变量 Lt 说明叶节点 t 中误分类观察的数量,即不属于该叶节点中代表最多的类的观察数量。这些变量使我们能够计算训练样本中错误分类观察的总数。因此,模型要最小化的数量由以下总和给出:
分支节点处基于距离的错误:每次向树添加拆分时,都会合并一个基于 SVM 的超平面,其中基于全局便利性为整个树分配标签。因此,我们在 Tb 中的每个分支节点处测量 SVM 分类器在该分割处产生的基于距离的误差。该数量由 eit 变量测量,并通过总和合并到模型中:

树的复杂性:生成的树的简单性是通过在其构造中完成的拆分数量来衡量的。由于 dt 变量告诉我们节点 t 是否被拆分,因此该术语在我们的模型中被解释为:
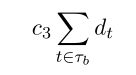
总而言之,我们模型的总体目标函数是:
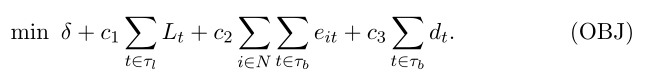
请注意,系数 c1、c2 和 c3 分别权衡了训练样本的错误分类、类之间的分离和树的复杂性。应该仔细校准这些参数,以便构建具有高预测能力的简单决策树,如我们的计算实验所示。
4.3 约束
通过定义数学规划模型的以下约束来描述对变量之间关系的要求和我们模型的基本原理。首先,为了充分表示分裂超平面的逆边距中的最大值,我们需要:

接下来,我们强加如何在树中执行拆分。为此,我们需要知道哪些观测值属于某个节点 t(z 变量),以及这些观测值是如何相对于要分离的两个虚构类(α 变量)分布的。将所有这些元素聚集在一起,我们使用以下约束来定义决策树的拆分:
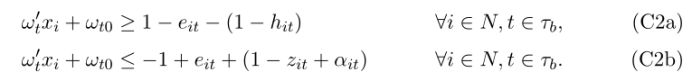
据此,只有在观察 i 属于参考类并且它位于节点 t 中(hit = 1)的情况下,才会激活约束(C2a)。另一方面,如果 i 被分配给节点 t (zit = 1) 但它不属于参考类 (αit = 0),则 (C2b) 被激活。因此,参考类位于超平面 Ht 的正半空间,而另一个类位于负半空间,同时,边缘违规由 eit 变量调节。
为了确保上述约束的正确行为,我们必须正确定义 zit 变量。首先,要求每个观测值恰好属于树中每一层的一个节点。这可以通过在树的每个级别 u ∈ U 上向问题添加通常的分配约束来轻松完成:
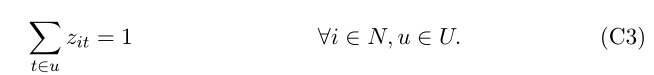
此外,我们应该强制如果观察 i 在节点 t (zit = 1) 中,那么观察 i 也必须在 t 的父节点中,p(t) (zip(t) = 1),并且观察 i 也可以如果它不在其父节点中,则不在节点 t 中 (zip(t) = 0 ? zit = 0)。这些含义可以通过以下约束获得:
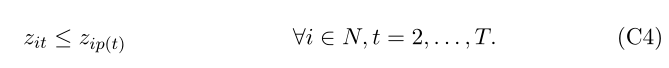
然而,观察通过树下降的方式需要进一步分析,因为此时他们可以随机定义树中的路径。每当观察 i 在节点 t, Ht 处的分裂超平面的正半空间中时,该观察应该遵循连接到 t 的子节点的右分支。否则,如果 i 在负半空间上,它应该跟随左分支。观察所属的分裂超平面一侧的知识被编码在α变量中。然后,如果 i 位于 Ht 的正半空间,则 αit 永远不会等于 0,因为它会导致 eit 的值大于 1,而在 αit = 1 的情况下保证 eit < 1。
通过上述观察,确保分裂超平面相对于观察所属的一侧正确构造的约束如下:


约束 (C5a) 确保如果观察 i 位于偶数节点 t (zip(t) = 1) 的父节点上,并且 i 位于 Hp(t) 的负半空间上 (αip(t) = 0),然后 zit 被强制等于一。结果,αip(t) = 0 迫使观察 i 采取节点 t 中的左分支。注意,如果 zip(t) = 1,同时观察 i 不在 t 的左子节点中(zit = 0 for i ∈ τbl),则 αip(t) = 1,这意味着观察 i位于 Hp(t) 的正半空间。约束 (C5b) 类似于 (C5a) 但允许充分表示右分支节点。

此外,需要结合两个额外的重要元素来完成我们的模型:树的复杂性和错误分类观察的正确定义。请注意,在通常不使用基于 SVM 的拆分的最佳分类树中,只需在所有分支节点中强制 kωtk22 ≤ M dt (对于足够大的 M 常数),就可以轻松调节复杂性,因为如果一个节点不是进一步分支(dt = 0),分裂超平面的系数设置为零。然而,在我们的例子中,分裂超平面是基于 SVM 的超平面,这些约束与约束 (C2a) 和 (C2b) 冲突,因为在 dt = 0(因此 ωt = 0)的情况下,它不仅意味着系数 ωt 等于 0,而且基于距离的误差将设置为最大值 1,即对于节点中的每个观测值 i,eit = 1,即使这些误差没有任何意义,因为观测值不会在节点处分离。为了克服这个问题,我们考虑辅助二元变量 hit = zitαit(如果观察 i 属于节点 t 并且位于应用于节点 t 的分裂超平面的正半空间中,则命中取值为 1)和 vt(取值为零如果节点中的所有点都属于正半空间,否则一个)。如果将以下约束合并到模型中,则可以充分定义变量: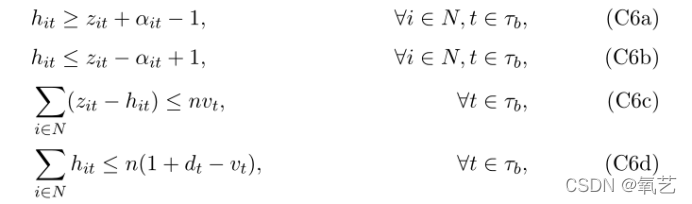
其中约束 (C6a) 和 (C6b) 是双线性约束 hit = zitαit 的线性化。另一方面,约束 (C6c) 确保在 vt = 0 的情况下,节点 t 中的所有观察值都属于 Ht 的正半空间,并且约束 (C6d) 确保如果 vt = 1 并且树在节点 t 处被修剪(dt = 0),那么分配给节点 t 的那些观测值被放置在由分裂超平面定义的负半空间中。因此,它意味着当且仅当节点 t 中的观察被 Ht 分隔时,dt 取值 1,因此在节点处产生有效分割。
最后,为了充分表示 Lt 变量(测量叶节点上错误分类观察次数的变量),我们使用 [8] 中的 OCT-H 模型中已经包含的约束。一方面,我们将每个叶节点分配给一个类(属于该节点的最流行的观察类)。我们使用二进制变量 qkt 来检查叶节点 t ∈ τl 是否分配给类 k = 1, 。 . . , K. 通常的分配约束被认为是为了确保每个节点都被分配给一个类:
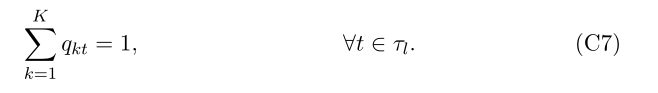
然后通过以下一组约束来保证变量 Lt 的正确定义:
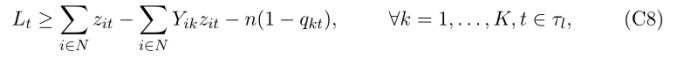
当且仅当 qkt = 1 时,这些约束才被激活,即,如果节点 t 中的观察值被分配给类 k。在这种情况下,由于 Lt 在目标函数中被最小化,Lt 将由节点 t 中除标签为 k 的训练观测值外的训练观测数确定,即节点 t 中的错误分类观测数根据 k-课堂作业。
观察到 (C8) 中的常数 n 可以减小并固定为训练样本中错误分类观察值的最大数量。这个数字与训练样本中的观测数 (n) 与样本中最具代表性的类别中的观测数之差一致。
总结以上段落,MOCTSVM 可以表述为以下 MINLP 问题: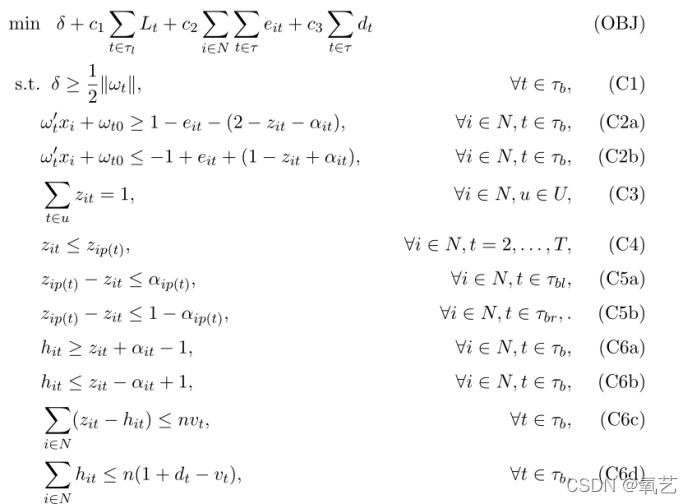
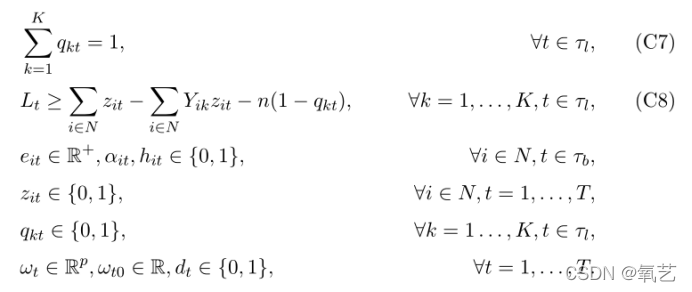
4.4 强化示范
上面介绍的 MINLP 公式对我们的 MOCTSVM 模型有效。然而,这是一个计算成本很高的问题,虽然它可以通过大多数现成的优化求解器(如 Gurobi、CPLEX 或 XPRESS)来解决,但它只能以最佳方式解决中小型实例。为了提高其性能,可以通过有效不等式来加强问题,这允许人们减少问题的连续松弛与其最佳整数解之间的差距,然后能够在更短的 CPU 时间内解决更大的实例。在下文中,我们将描述我们已纳入 MINLP 公式的其中一些不等式:
如果观察 i 和 i’ 属于不同的节点,则它们不能分配给树的其余级别的同一节点:
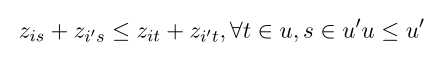
如果叶节点 t 和 s 是适当分裂超平面的结果,则不能将两个节点分配给同一类:
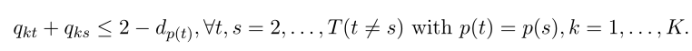
在 zit = 0 的情况下,变量 αit 强制取值为 0:
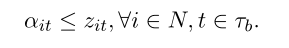
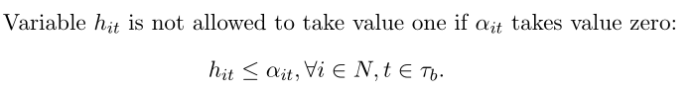
如果 αit 取值为零,则变量 hit 不允许取值 1:
每个类都应该至少有一个叶节点(假设每个类都在训练样本中表示)。这也意味着一个类被分配到的节点的数量有界为:
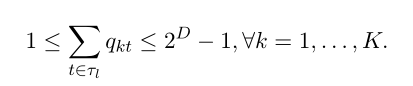

为了降低维度并避免 MINLP 问题的对称性,还可以应用一些启发式策略来在预处理阶段固定一些二进制变量的值。例如,我们选择 i0 ∈ arg maxi∈N | {i0 ∈ N : kai ? ai0k ≤ ε and yi = yi0} | ,即在同一类中具有最大观察量的观察值与其足够接近。然后,我们将 i ∈ {i0 ∈ N : kai?ai0k ≤ ε 和 yi = yi0} 的所有变量 zit0 固定为一个,将 t0 作为树的第一个左叶节点(并将这些点的分配固定为零)其余的叶节点)。类似地,我们也将所有 z 变量固定为一个,将观察分配给树的最后一个右叶节点,用于同一类中距离 i0 足够远的观察子集,即对于所有 i ∈ {i0,zitf = 1 ∈ N : kaif ? ai0k ≤ ε and yif = yi0} 其中 if = arg maxi∈N kai0 ? aik (并将这些点分配给其余叶节点的固定为零)。
5.实验
为了分析这种新方法的性能,我们在来自 UCI 机器学习存储库 [3] 的不同真实数据集之间进行了一系列实验。我们选择了 12 个数据集,类别数在 2 到 7 之间。这些问题的维度在表 3 中由元组报告(n:观察数,p:特征数,K:类数)。
我们将 MOCTSVM 模型与其他三种基于分类树的方法进行了比较,即 CART、OC??T 和 OCT-H。所有模型的最大树深度 D 等于 3,CART、OC??T 和 OCT-H 中每个节点的最小观察数等于训练规模的 5%
我们对每个实例执行了 5 折交叉验证方案,即数据集被分成五个随机训练测试分区,其中一个折叠用于构建模型,其余用于测量模型的准确性预测。此外,为了避免利用有益的初始分区,我们对所有数据集重复了五次交叉验证方案。
CART 方法是使用 rpart 库在 R 中编码的。另一方面,MOCTSVM、OCT 和 OCT-H 用 Python 编码,并使用优化求解器 Gurobi 8.1.1 求解。所有实验均在 PC Intel Xeon E-2146G 处理器上运行,频率为 3.50GHz,内存为 64GB。训练折叠的训练时间限制为 300 秒。尽管并非所有问题都在时限内得到最佳解决,但如表 3 所示,使用我们的模型获得的结果已经优于其他方法。
为了校准调节树复杂性的不同模型的参数,我们使用了不同的方法。

一方面,对于 CART 和 OCT,由于这种深度的最大节点数是 2D - 1 = 7,因此可以通过在网格中搜索来搜索具有最佳复杂度的树 ?1,…。 . . , 2D - 1?可能的活动节点。对于 OCT-H,我们在网格 ?10i 中搜索复杂性正则化因子:i = -5, . . . , 5?。最后,在 MOCTSVM 中,我们使用了相同的网格 ?10i:i = -5, 。 . . , 5?对于 c1 和 c2,以及?10i:i = -2,. . . , 2?对于 c3。
在表 3 中,我们报告了在所有模型的实验中获得的结果。表的第一列表示数据集的标识(连同它的维度)。其次,对于我们测试过的每种方法,我们都会报告获得的平均测试准确度和标准偏差。我们以粗体突出显示为每个数据集获得的最佳平均测试精度。
可以看出,在大多数情况下,我们的方法在准确性方面明显优于其他方法。显然,我们的模型旨在构建具有更大类间距的最优分类树,从而提高测试样本的准确性。数据集 Australian 和 BalanceScale 使用 OCT-H 获得了更好的结果,但是可以观察到,与其他方法的差异很小(这是在测试样本中正确分类的结果,只是比其余方法)。在这种情况下,我们的方法获得的准确度几乎与 OCT-H 一样好。在其余数据集中,我们的方法始终获得更好的分类器,例如对于皮肤病学,与其他最佳分类器的差异在 [4%, 19%] 范围内,对于帕金森,我们模型的准确度至少为 6比其他模型好 %,对于 Wine,我们的准确度比 OCTH 高 5%,比 CART 高 10%,对于 Zoo,我们模型的准确度比 CART 高 17% 以上。
关于我们方法的可变性,表 3 中报告的标准偏差表明,平均而言,我们的结果比其他结果更稳定,平均精度偏差很小。这种行为不同于在 CART 或 OCT 中观察到的行为,后者会获得更大的偏差,这意味着准确度高度取决于应用该方法的测试文件夹。
6. 结论和进一步研究
我们在本文中提出了一种通过数学规划模型为多类实例构建分类器的新方法。所提出的方法输出分类树是基于支持向量机的超平面的分裂。在树的每个分支节点,构造一个二元 SVM 超平面,其中观察被分类为两个虚构的类(在所有分裂节点中忽略原始类),但测量树的全局优度在叶节点处,错误分类错误被最小化。此外,该模型将树的复杂性与 SVM 方法中出现的两个元素一起最小化:边缘分离和基于距离的错误分类错误。我们进行了大量的计算实验,表明我们的方法在准确性和稳定性方面都优于大多数基于决策树的方法。
我们在本文中提出了一种通过数学规划模型为多类实例构建分类器的新方法。所提出的方法输出分类树是基于支持向量机的超平面的分裂。在树的每个分支节点,构造一个二元 SVM 超平面,其中观察被分类为两个虚构的类(在所有分裂节点中忽略原始类),但测量树的全局优度在叶节点处,错误分类错误被最小化。此外,该模型将树的复杂性与 SVM 方法中出现的两个元素一起最小化:边缘分离和基于距离的错误分类错误。我们进行了大量的计算实验,表明我们的方法在准确性和稳定性方面都优于大多数基于决策树的方法。
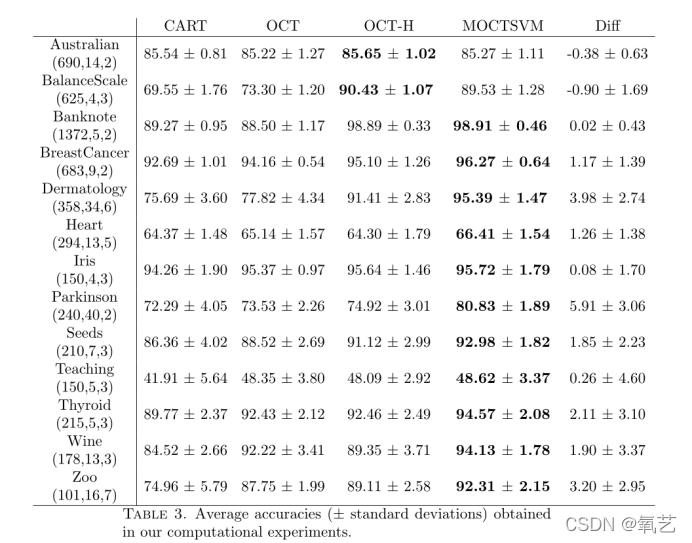
表3在我们的计算实验中获得的平均准确度(±标准偏差)。
关于这个主题的未来研究方向包括在 MOCTSVM 中分支时的非线性分裂分析,两者都使用从 SVM 分类器或特定非线性分离器系列派生的内核工具。这种方法将产生更灵活的分类器,能够捕捉许多现实生活数据集的非线性趋势。此外,我们还计划在我们的方法中加入特征选择,以构建具有高度预测性但也更具可解释性的分类工具。
致谢
参考文献
[1] Agarwal, N., Balasubramanian, V. N., and Jawahar, C. Improving multiclass classification by deep networks using dagsvm and triplet loss. Pattern Recognition Letters 112(2018), 184–190.
通过使用 dagsvm 和三元组损失的深度网络改进多类分类
[2] Allwein, E. L., Schapire, R. E., and Singer, Y. Reducing multiclass to binary: A unifying approach for margin classifiers. Journal of machine learning research 1, Dec (2000), 113–141.
边缘分类器的统一方法
[3] Asuncion, A., and Newman, D. Uci machine learning repository, 2007.
机器学习存储库
[4] Bahlmann, C., Haasdonk, B., and Burkhardt, H. Online handwriting recognition with support vector machines-a kernel approach. In Proceedings Eighth International Workshop on Frontiers in Handwriting Recognition (2002), IEEE, pp. 49–54.
支持向量机的在线手写识别——一种内核方法
[5] Baldomero-Naranjo, M., Mart′?nez-Merino, L. I., and Rodr′?guez-Ch′?a, A. M. Tightening big ms in integer programming formulations for support vector machines with ramp loss. European Journal of Operational Research 286, 1 (2020), 84–100.
在具有斜坡损失的支持向量机的整数规划公式中紧缩大ms
[6] Baldomero-Naranjo, M., Mart′?nez-Merino, L. I., and Rodr′?guez-Ch′?a, A. M. A robust svm-based approach with feature selection and outliers detection for classification problems. Expert Systems with Applications 178 (2021), 115017.
基于svm的分类问题特征选择和异常值检测方法
[7] Ben′?tez-Pe?na, S., Blanquero, R., Carrizosa, E., and Ram′?rez-Cobo, P. Costsensitive feature selection for support vector machines. Computers & Operations Research 106 (2019), 169–178.
支持向量机代价敏感特征选择
[8]Bertsimas, D., and Dunn, J. Optimal classification trees. Machine Learning 106, 7 (2017), 1039–1082.
最优分类树
[9] Bertsimas, D., and Dunn, J. W. Machine learning under a modern optimization lens, 2019.
现代优化镜头下的机器学习
[9]Blanco, V., Japón, A., and Puerto, J. A mathematical programming approach to binary supervised classification with label noise. arXiv preprint arXiv:2004.10170 (2020).
现代优化视角下的机器学习
[11] Blanco, V., Japón, A., and Puerto, J. Optimal arrangements of hyperplanes for svmbased multiclass classification. Advances in Data Analysis and Classification 14, 1 (2020), 175–199.
数据分析与分类进展
[12]Blanco, V., Japón, A., and Puerto, J. Robust optimal classification trees under noisy labels. Advances in Data Analysis and Classification (2021).
数据分析和分类的进展
[13]Blanco, V., Puerto, J., and Rodriguez-Chia, A. M. On lp-support vector machines and multidimensional kernels. J. Mach. Learn. Res. 21 (2020), 14–1.
关于支持向量机和多维核的研究
[14] Blanquero, R., Carrizosa, E., Molero-R′?o, C., and Morales, D. R. Optimal randomized classification trees. Computers & Operations Research 132 (2021), 105281.
最优随机分类树
[15] Breiman, L., Friedman, J., Olshen, R., and Stone, C. Classification and regression trees, 1984.
分类和回归树
[16] Carrizosa, E., Molero-R′?o, C., and Morales, D. R. Mathematical optimization in classification and regression trees. Top 29, 1 (2021), 5–33.
在分类和回归树中的数学优化
[17] Cortes, C., and V apnik, V. Support-vector networks. Machine learning 20, 3 (1995), 273–297.
支持向量网络
[18] Cover, T., and Hart, P. Nearest neighbor pattern classification. IEEE transactions on information theory 13, 1 (1967), 21–27.
最近邻模式分类
[19] Crammer, K., and Singer, Y. On the algorithmic implementation of multiclass kernelbased vector machines. Journal of machine learning research 2, Dec (2001), 265–292.
关于基于多类核的向量机的算法实现
[20] Dietterich, T. G., and Bakiri, G. Solving multiclass learning problems via errorcorrecting output codes. Journal of artificial intelligence research 2 (1994), 263–286.
通过纠错输出码解决多类学习问题
[21] Du, M., Liu, N., and Hu, X. Techniques for interpretable machine learning. Communications of the ACM 63, 1 (2019), 68–77.
一种可解释的机器学习方法
[22] Eitrich, T., and Lang, B. Efficient optimization of support vector machine learning parameters for unbalanced datasets. Journal of computational and applied mathematics 196, 2 (2006), 425–436.
不平衡数据集支持向量机学习参数的有效优化
[23] Friedman, J., Hastie, T., and Tibshirani, R. The elements of statistical learning, 2001.
统计学习的要素
[24] Gan, J., Li, J., and Xie, Y. Robust svm for cost-sensitive learning. Neural Processing Letters (2021), 1–22.
代价敏感学习的鲁棒支持向量机
[25] Gaudioso, M., Gorgone, E., Labbé, M., and Rodr′?guez-Ch′?a, A. M. Lagrangian relaxation for svm feature selection. Computers & Operations Research 87 (2017), 137–145.
基于拉格朗日松弛的svm特征选择方法
[26] Guermeur, Y., and Monfrini, E. A quadratic loss multi-class svm for which a radius– margin bound applies. Informatica 22, 1 (2011), 73–96.
一个应用半径边界的二次损失多类支持向量机
[27] Günlük, O., Kalagnanam, J., Menickelly, M., and Scheinberg, K. Optimal decision trees for categorical data via integer programming. arXiv preprint arXiv:1612.03225 (2018).
通过整数规划的分类数据的最优决策树
[28] Harris, T. Quantitative credit risk assessment using support vector machines: Broad versus narrow default definitions. Expert Systems with Applications 40, 11 (2013), 4404– 4413.
使用支持向量机的量化信用风险评估:广义与狭义违约定义
[29] Hastie, T. J., and Tibshirani, R. J. Generalized additive models, 2017.
广义可加模型
[30] Jiménez-Cordero, A., Morales, J. M., and Pineda, S. A novel embedded min-max approach for feature selection in nonlinear support vector machine classification. European Journal of Operational Research 293, 1 (2021), 24–35.
一种新的嵌入最小-最大方法用于非线性支持向量机分类
[31] Kaˇs′celan, V., Kaˇs′celan, L., and Novovi′c Buri′c, M. A nonparametric data mining approach for risk prediction in car insurance: a case study from the montenegrin market. Economic research-Ekonomska istraˇ zivanja 29, 1 (2016), 545–558.
汽车保险风险预测的非参数数据挖掘方法:以黑山市场为例
[32] Lauer, F., and Guermeur, Y. Msvmpack: a multi-class support vector machine package. The Journal of Machine Learning Research 12 (2011), 2293–2296.
Msvmpack:一个多类支持向量机包
[33] Lee, Y., Lin, Y., and W ahba, G. Multicategory support vector machines: Theory and application to the classification of microarray data and satellite radiance data. Journal of the American Statistical Association 99, 465 (2004), 67–81.
基于多类别支持向量机的卫星辐射数据分类方法研究
[34] Letham, B., Rudin, C., McCormick, T. H., and Madigan, D. Interpretable classifiers using rules and bayesian analysis: Building a better stroke prediction model. The Annals of Applied Statistics 9, 3 (2015), 1350–1371
使用规则和贝叶斯分析的可解释分类器:建立一个更好的中风预测模型
[35] Lewis, D. D. Naive (bayes) at forty: The independence assumption in information retrieval. In European conference on machine learning (1998), Springer, pp. 4–15.
贝叶斯:信息检索中的独立性假设
[36] Majid, A., Ali, S., Iqbal, M., and Kausar, N. Prediction of human breast and colon cancers from imbalanced data using nearest neighbor and support vector machines. Computer methods and programs in biomedicine 113, 3 (2014), 792–808.
使用最近邻和支持向量机从不平衡数据预测人类乳腺癌和结肠癌
[37] Meyer, D., Dimitriadou, E., Hornik, K., Weingessel, A., Leisch, F., Chang, C., and Lin, C. Misc functions of the department of statistics, probability theory group (formerly: E1071). Package e1071. TU Wien (2015).
统计学系的Misc函数,概率论群
[38] Pedregosa, F., V aroquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P., Weiss, R., Dubourg, V., et al. Scikit-learn: Machine learning in python. the Journal of machine Learning research 12 (2011), 2825– 2830.
Scikit-learn: python中的机器学习
[39] Quinlan, J. Machine learning and id3. Los Altos: Morgan Kauffman (1996).
机器学习和id3
[40] Quinlan, R. C4. 5. Programs for machine learning (1993).
机器学习程序
[41] Radhimeenakshi, S. Classification and prediction of heart disease risk using data mining techniques of support vector machine and artificial neural network. In 2016 3rd International Conference on Computing for Sustainable Global Development (INDIACom) (2016), IEEE, pp. 3107–3111.
基于支持向量机和人工神经网络数据挖掘技术的心脏病风险分类和预测
[42] Tang, X., and Xu, A. Multi-class classification using kernel density estimation on knearest neighbours. Electronics Letters 52, 8 (2016), 600–602.
基于最近邻核密度估计的多类分类方法
[43] van den Burg, G., and Groenen, P. Gensvm: A generalized multiclass support vector machine. Journal of Machine Learning Research 17 (2016), 1–42.
广义多类支持向量机
[44] Weston, J., and W atkins, C. Support vector machines for multi-class pattern recognition. In Esann (1999), vol. 99, pp. 219–224.
基于支持向量机的多类别模式识别
[1] Blanco V , A Japón, Puerto J . Multiclass Optimal Classification Trees with SVM-splits[J]. 2021.