[人工智能]使用Sklearn进行线性回归和二次回归的比较（基于jupyter）

以简单的披萨直径与价格的线性回归方程和二次回归方程举例，利用sklearn进行拟合与可视化处理。其中涉及到利用PolynomialFeatures的方法将给定一维数据集转换为多项式形式。

1、首先导入所需要的库包

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures

2、简单预设数据集

X_train = [[6],[8],[10],[14],[18]]
y_train = [[7],[9],[13],[17.5],[18]]
X_test = [[6],[8],[11],[17]]
y_test = [[8],[12],[15],[19]]

3、以线性回归的方式对模型进行拟合训练

regressor = LinearRegression()
regressor.fit(X_train,y_train)

4、生成多项式特征（最高次为2），并拟合二次回归曲线

quadratic_featurizer = PolynomialFeatures(degree=2)
X_train_quadratic = quadratic_featurizer.fit_transform(X_train)

regressor_quadratic = LinearRegression()
regressor_quadratic.fit(X_train_quadratic,y_train)

5、为了可视化两种方式对拟合性，生成100个数据点描绘图形

xx = np.linspace(0,26,100) # 在0-26区间内生成100个点
# print（xx）
# xx.reshape(xx.shape[0],1)意味着将点转换为一维数据形式
yy = regressor.predict(xx.reshape(xx.shape[0],1)) 
#print(xx.reshape(xx.shape[0],1))

xx_quadratic = quadratic_featurizer.transform(xx.reshape(xx.shape[0],1))
yy_quadratic = regressor_quadratic.predict(xx_quadratic)

其中xx.shape为（100，），xx.reshape(xx.shape[0],1).shape为（100，1），xx_quadratic.shape为（100，3），注意?PolynomialFeatures(degree=2)是生成（1，x，x^2)三列数据。

6、利用plt画出两组回归曲线

plt.figure()
plt.title(u"the plot of pizza")
plt.xlabel(u"size")
plt.ylabel(u"prize")
plt.axis([0,25,0,25])
plt.grid(True)
plt.scatter(X_train,y_train,s=40)
plt.plot(xx,yy,label="linear equation")
plt.plot(xx,yy_quadratic,"r-",label = "quadratic equation")
plt.legend(loc="upper left")
plt.show()

最终运行结果如下

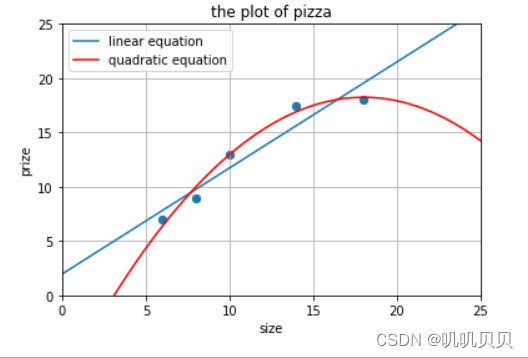
?7、为检验两组曲线拟合效果，利用R方进行验证

X_test_quadratic = quadratic_featurizer.transform(X_test)
print("linear equation r_squared",regressor.score(X_test,y_test))
print("quadratic equation r_squared",regressor_quadratic.score(X_test_quadratic,y_test))

最终得到结果

?该文章代码引自中国慕课网课程深度学习基础_哈尔滨工业大学_中国大学MOOC(慕课) (icourse163.org)