[人工智能]leastsq函数的使用

leastsq作用：最小化一组方程的平方和。
参数设置：
func 误差函数
x0 初始化的参数
args 其他的额外参数

举个例子就清楚了
首先创建样本点

import numpy as np
import scipy as sp
from scipy.optimize import leastsq
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
x=[1,2,3,4]
y=[2,3,4,5]

拟合直线

def y_pre(p,x):
    f=np.poly1d(p)
    return f(x)

其中的np.polyld

f=np.poly1d([1,2,3])
 # x^2+2x+3
f(1)
"""
6
"""

误差函数

def error(p,x,y):
    return y-y_pre(p,x)

接下就简单了

p=[1,2]    # 值随便写
# y=w1*x+w2
res=leastsq(error,p,args=(x,y))
w1,w2=res[0]   # res[0]中就是wi的参数列表
"""
到这w1和w2就已经求出来了，下面是画图看一下
"""
x_=np.linspace(1,10,100)   # 等差数列，
y_p=w1*x_+w2               # 求出的拟合曲线
plt.scatter(x,y)           # 样本点
plt.plot(x_,y_p)           # 画拟合曲线

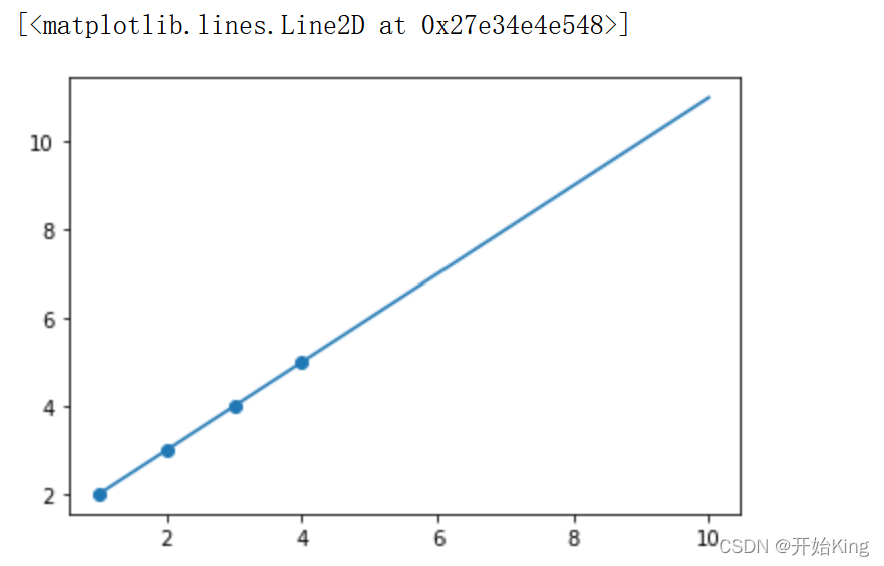
可以直接封装成函数

x=np.linspace(0,2,10)
y=np.sin(np.pi*x)
# 原始的样本
y_=[y + np.random.normal(0,0.1) for y in y]     # np.random.normal(loc,scale,size):正态分布的均值,正态分布的标准差,形状

# np.random.randn()   # 标准正态分布是以0为均数、以1为标准差的正态分布，记为N（0，1）

def fit(M=1):
    p=np.random.rand(M+1)   # 返回一个或一组服从“0~1”均匀分布的随机样本值。随机样本取值范围是[0,1)
    res=leastsq(error,p,args=(x,y))  # wi 的值
    x_point=np.linspace(0,2,100)  # 增加数据量为了画出的图平滑
    y_point=np.sin(np.pi*x_point) # 增加数据量为了画出的图平滑
    plt.plot(x_point,y_point,'r',label='原始')
    plt.plot(x_point,y_pre(res[0],x_point),'b',label='拟合')
    plt.scatter(x,y_)
    plt.legend()
fit(3)

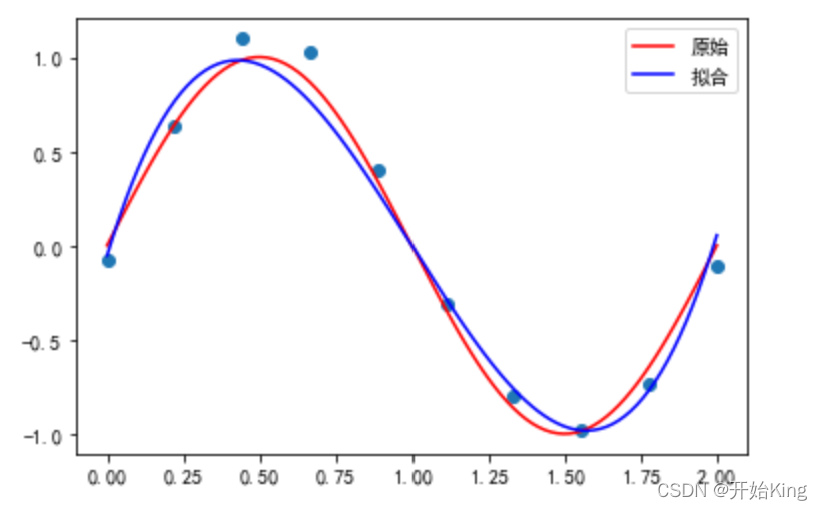
你也可以输出一下中间的结果

x=np.linspace(0,2,10)
y=np.sin(np.pi*x)
# 原始的样本
y_=[y + np.random.normal(0,0.1) for y in y]     # np.random.normal(loc,scale,size):正态分布的均值,正态分布的标准差,形状

# np.random.randn()   # 标准正态分布是以0为均数、以1为标准差的正态分布，记为N（0，1）

def fit(M=1):
    p=np.random.rand(M+1)   # 返回一个或一组服从“0~1”均匀分布的随机样本值。随机样本取值范围是[0,1)
    res=leastsq(error,p,args=(x,y))  # wi 的值
    x_point=np.linspace(0,2,100)
    y_point=np.sin(np.pi*x_point)
    plt.plot(x_point,y_point,'r',label='原始')
    plt.plot(x_point,y_pre(res[0],x_point),'b',label='拟合')
    print(res[0])
    plt.scatter(x,y_)
    plt.legend()
fit(3)

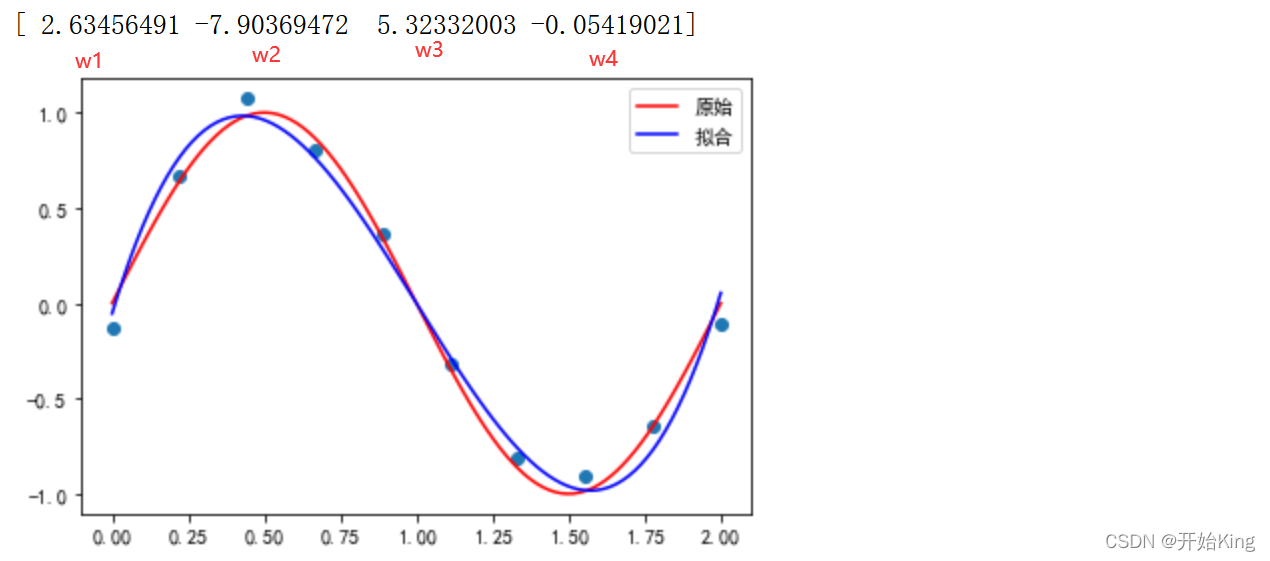拟合的直线就是
$y=w_1?x^3+w_2?x^2+w3?x^1+w_4?x^0$