时间序列模型简介
??尽管此前我们已经用到了time series这个专业名词,但我们对时序特征进行的处理,并不是time series这个专业名词所代表的真正含义,既时间序列。尽管本阶段我们并不会讲解时间序列模型,但既然讨论了时序特征,对时间序列略加了解,也是能够增加对时序特征处理方法理解的。因此以下部分作为补充内容,简单介绍下到底什么是时间序列模型。
注,此处仅对时间序列分析模型进行简单介绍,而时间序列分析模型本身也只是针对时序数据进行分析的诸多模型中的一种,其他能够进行时序规律挖掘的模型还包括RNN、LSTM等。
- 什么是时间序列模型
??首先时间序列模型是一类拥有非常强统计背景的模型,尽管也属于有监督学习范畴,但其建模过程和机器学习的有监督学习算法大相径庭。时间序列是一种用于进行回归问题建模的模型,整个建模过程只有时间这一个特征,也就是说时间序列的模型预测过程就是希望通过时间这一个特征去对标签进行连续型数值预测。
- 时间序列模型的建模过程
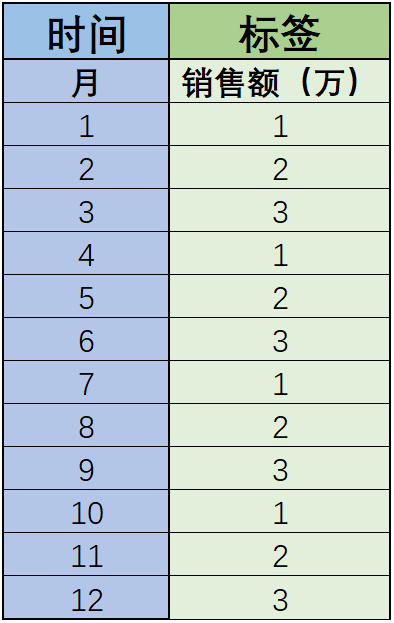
??为了更好的理解时间序列模型,我们通过一组简单的例子来展示时间序列模型的一般建模过程。首先假设有如下数据集,特征只有月份这一个时间,标签是销售额,具体数值如下所示:
 ??
??
对于上述数据集,特征和标签就不是简单的相关关系了。通过观察我们不难看出,标签的取值呈周期性变化,并且如果我们进一步将月份按照自然周期进行季度的划分,则会发现有如下规律:
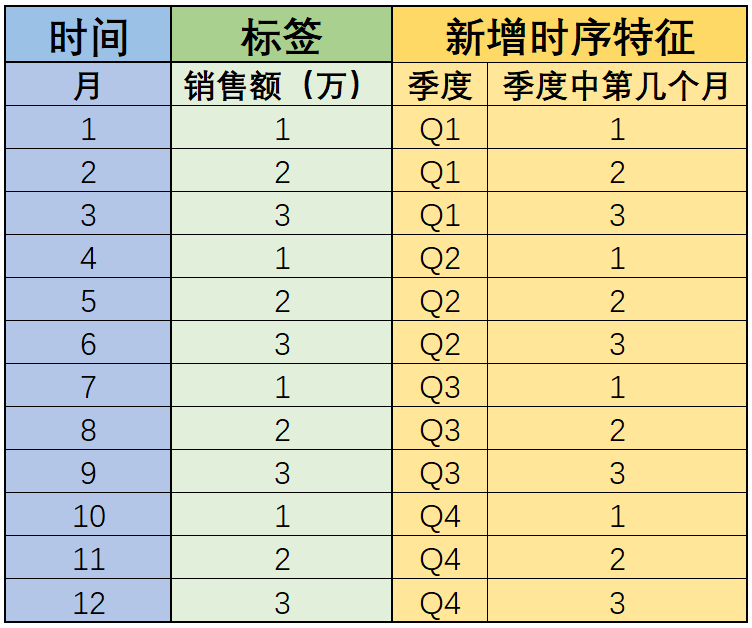
即销售额不再和月份相关,而是和每个季度的第几个月呈现出相关关系,那么也就是说,如果是围绕上述数据集进行预测,我们只需要将自然周期的月按照季度来进行划分,然后创建“季度中的第几个月”字段,即可利用该字段对销售额进行预测。当然,这种相关性还有另一种能够更加深刻的描述其本质的概念:自相关。
??所谓自相关,指的是标签自己和自己相关,并且指的是某个时间点的自己和之前一段时间的自己是相关的。例如在上述数据集中,每个标签的取值,其实就和一个季度前的自己有极大的相关性(甚至取值都是一样的):
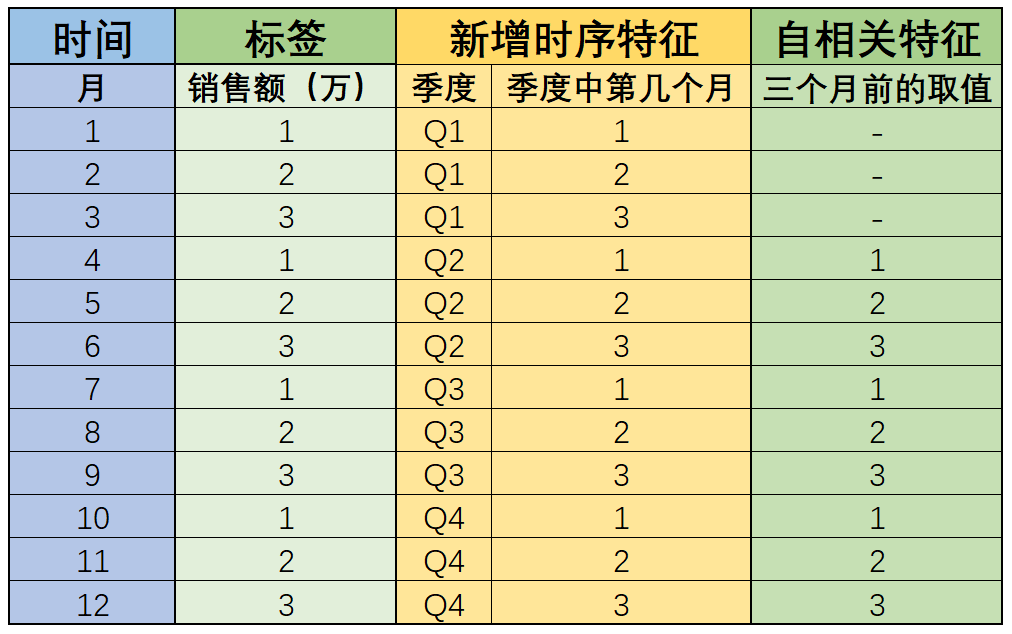
而标签一定要在时间维度上呈现出一定的自相关性,才能进一步带入时间序列模型进行建模预测。此外,这里的三个月时间差,也被称为按月计算的三阶差分,这里的销售额受到季节影响,也被称为销售额呈现季节性波动。
此处介绍的自相关性并不是自相关性概念的严谨定义、而自相关的概念也不仅仅出现在时间序列技术范畴内,望知悉。
??当然,类似上述例举的,完全的自相关的情况还是比较少,更常见的情况是存在自相关、但也并不是完全自相关,例如如下数据集情况:
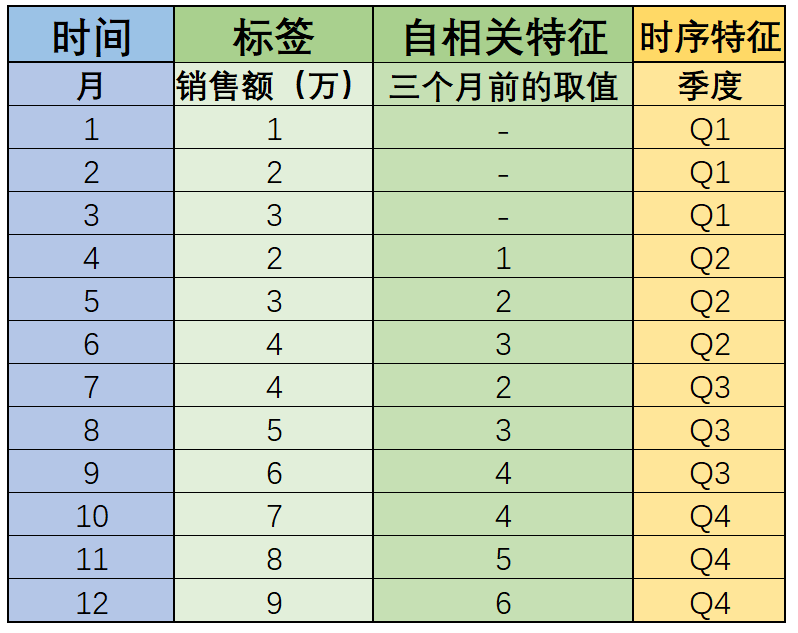
能够看出,该数据集的标签在时间特征上仍然呈现出一定的自相关性,但这种相关性只存在于一个季度内,“三个月前的自己”和“现在的自己”都呈现出季度内稳步增长的情况,但也只是变化的趋势相同,Q2、Q1季度之间每月都相差1,而Q3和Q2之间每月则相差2,Q4和Q3之间每月相差3,哪怕间隔时间相同,随着时间变化,“过去的自己”和“现在的自己”差异也在逐渐增加,这种变化,也被称为时间序列中的趋势。对应到当前数据中来,就是整体序列的变化趋势是稳步增加的,即销售额尽管受到不同季度的季度周期影响,但整体是呈现上涨趋势的。
??而时间序列中存在一些“趋势”,也是非常常见的一种情况。当然,除了一些季节性波动、长期趋势以外,有些时候还会出现一些偶然因素导致的时间序列发生变化,例如数据集如下所示:
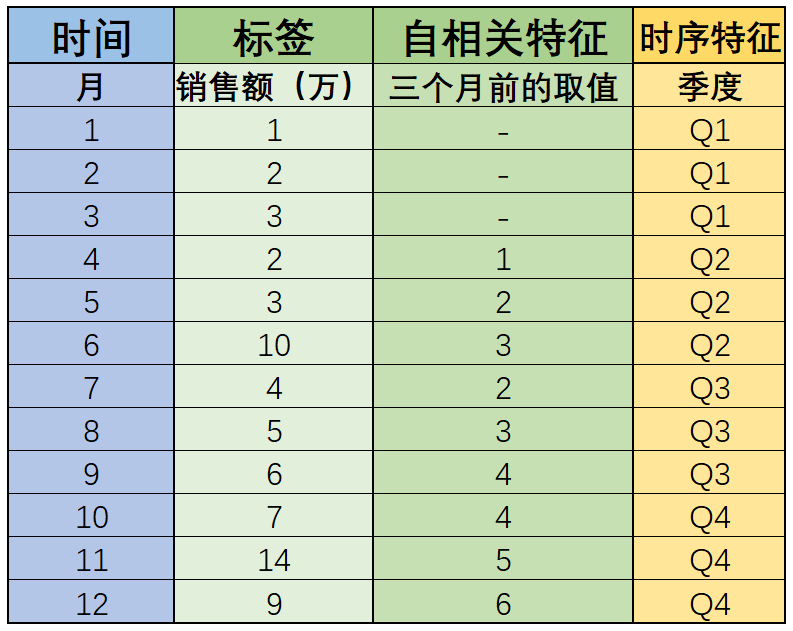
??首先,该数据的销售额仍然存在季节性波动,同时呈现整体上涨的趋势,但其中6月、11月两个月的销售额稍显异常,通过和之前的数据集对比不难发现,该数据集的6月、11月销售额都增长了6万,这很可能是商家在6月和11月分别举办了“618”和“双11”促销活动所导致的销售额增加,而这些事件,也被称为不确定事件(并不是通过自然周期划分所决定的),往往在进行时间序列预测时,我们都需要把这些对时间序列有明显影响的随机事件找出来,合理评估其对标签的影响,然后利用再对预测的时间序列进行修正。
??此外,在某些长期的预测项目中,还有可能出现一些循环的变动,例如某些行业受到经济周期影响,每个五到十年就会进行类似循环的变化,这也就是所谓的时间序列中的循环趋势。而对于时间序列模型来说,其根本作用就是去捕捉目标变量(标签)在时间维度中所呈现出来的季节波动、长期规律以及循环规律,然后再使用一些随机事件对标签取值进行修正,最后得出预测结果。当然,判断某数据集是否适合进行时间序列的建模,首先我们需要对其进行自相关性(以及偏自相关性)检验。
从另一个角度来说,时序特征的周期划分就是捕捉周期性、关键时间差值就是趋势性与不规则规律挖掘。
- 时间序列模型本身的有效性
??最后,我们来简单讨论时间序列模型本身的有效性。长期钻研机器学习的小伙伴肯定对只需要时间维度、这么一丁点数据就可以完成对标签数值预测的算法怀有迟疑态度,但实际上在我们的生产生活中,是存在很大一部分预测场景、能用且只能用时间序列模型来进行预测的。例如(很多小伙伴感兴趣的)股票预测,以及我个人曾经主导的四川省卫计委区域患病人次预测项目,也就是预测某地区的患病总人次。
??在这些预测场景中,我们很难采用一般的机器学习模型进行建模,其中最难的地方在于无法有效的提取特征。对于区域患病人次预测项目来说,影响一个地区患病总人数的有效特征是非常难以提取及评估的,患病总人次可能和当地卫生状况、人口结构、气候、出行、节假日等诸多因素有关,而这些特征,要么受到随机事件影响根本无法提取(如大规模出行所导致的交叉感染)、要么根本无法量化评估(如卫生状况),而如果要通过气候变化对未来的一周甚至数周的患病人次进行预测,则还要依赖高度准确的天气预测结果。因此通过提取特征的方法进行机器学习预测,可以说是难上加难。
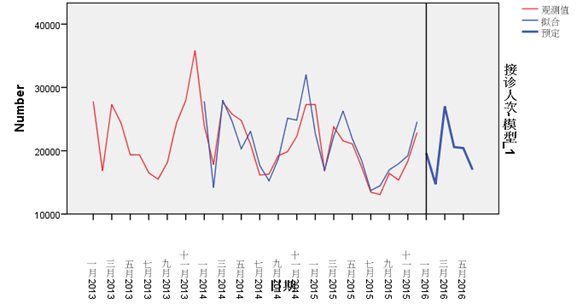
??而另一方面,尽管区域患病总人次会受到诸多不确定因素影响,但在一个较长的时间段中,整体患病人次在时间维度上的分布还是有一定规律的,如下所示:(下图为2013-2016年四川省某地区14岁以下非特慢疾病接诊人次序列)
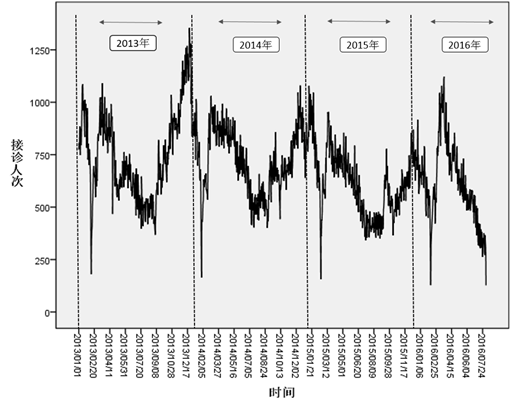
据此,我们可以进一步对其进行自相关性检测、时间序列建模、随机事件修正等,最终模型的实时预测(按月)平均误差率仅在5%以内,可以说是非常高精度的预测结果了。
- 时间序列的模型局限
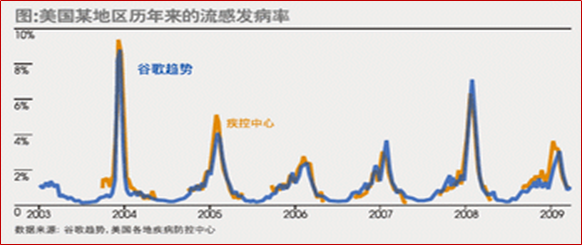
??当然,时间序列本身的局限也非常明显,或者说时间序列本身就是一种只适用于谋者特殊情况的模型,即当一系列的不确定性因素产生了某种综合性的确定性的影响之后,时间序列能够非常快速的对其进行规律挖掘,但如果预测项目可以有效提取特征,那么机器学习模型肯定是潜力更大的模型。同样是患病人次预测,谷歌通过借助搜索引擎的搜索结果来进行的全美冬季流感人数预测,就会更加先进、更加高效、更加精准。此外,如果标签并未在时间维度上呈现周期性波动、趋势性变化,也没有自相关性,那么时间序列模型也是无法构建的。
??当然,哪怕是数据分布规律符合时间序列模型建模要求,时间序列的预测周期也会极大受到既有数据时间跨度影响,例如我们要预测接下来一个季度每个月的患病人次,那么可能就需要有过去两年的历史数据的支持,而如果要预测半年的患病人次,则需要有至少3-4年的历史数据支持,而在很多信息化建设较晚的领域,如此时间跨度的历史数据的获取,本身可能也是不小的难度。