算法原理
在开始步入算法之前,可以很明显的看到回归的两字,这分类相比是另一类问题,而Sigmoid函数将回归问题也应用到了分类问题上来。
σ
(
z
)
=
1
1
?
e
?
z
\sigma(z)=\frac{1}{1-e^{-z}}
σ(z)=1?e?z1?
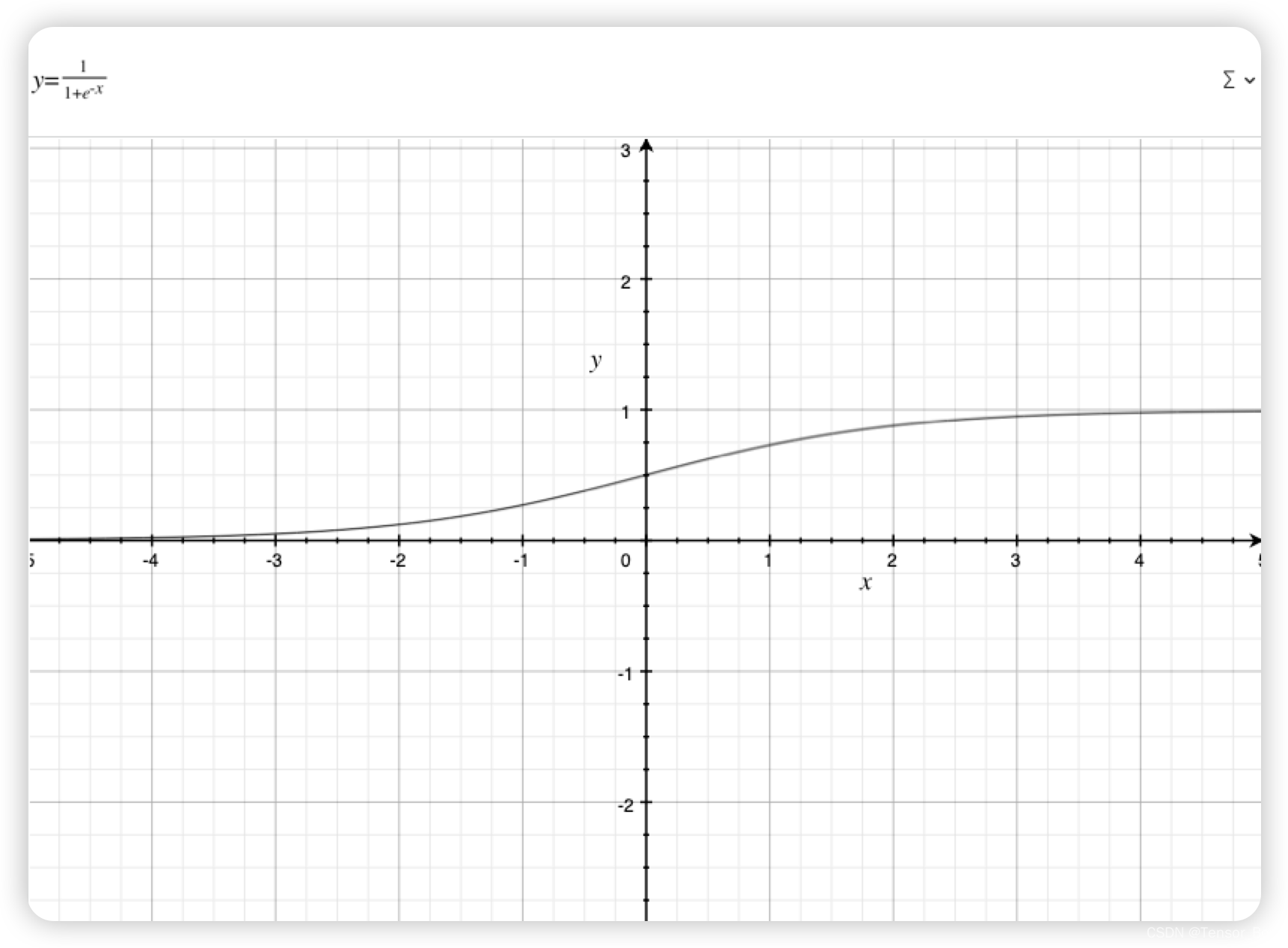
作出声明:Logistic是一个分类算法。
我们回顾一下之前的分类算法是什么样子。是通过样本的某一些特征来进行该样本的标签(Label),其特征往往是离散的数据,因为往往离散的数据是可以做到线性可划分的。
问题:那如果我们遇到是连续的数据将如何处理?
回归:非学术的解释是用一条直线对已知的点进行线性拟合,得到一条线形的方程类似于y=ax+b。
假设:在我们不知道摄氏度与华氏度之间的转换关系的时候,我们如何根据一些样本值来计算出这个公式呢?
F
=
a
C
+
b
F=aC+b
F=aC+b
当然我们可以通过百度得到a=1.8,b=32。但是现在我们有一部分数据(摄氏度,华氏度)这样子对应的数据,当然测量的本身是存在一定的误差,所以不能直接使用两个值来进行二元一次的方程的求解。所以在这个时候我们会用一条线就可能的去将所有的点都串到线上去。
这个过程就是拟合。这也是非常常用处理连续数据的方法。其中计算未知参数的时候可以采用梯度上升的方法或者是梯度下降的方法。
梯度上升:是一个利用偏导的方法来进行优化的方法。
往往我们在求解最小值或者最大时,通常会去计算倒数值为0的时候,因为这个时候的值处于一个没有增量的状态(稳定状态)。但由于已知数据存在测度误差无法直接找到最值,所以我们可以通过一个缓慢学习的过程来找到所需要的值,这个思想在深度学习中应用广泛。
y
=
w
x
+
b
y=wx+b
y=wx+b
我们在获得连续数据的方式之后,对于其分类通常能想到的是y大于某一个阀值的是就是某一类,或在某一个范围的时候。这里存在一个问题,y的值是不知道的,范围也是不知道的,这种情况是不利于求解的。
我们这里给出的解法也是仅适用于二分类的问题。我们可以看到sigmoid函数在越往正方向靠的时候越接近于1,越靠近负方向的时候越靠近0.同时处处可微,这是非常好的品质。也就是说我们可以使用梯度上升方法来进行优化算法。我们可以以0.5为阀值来进行分类,这样子就解决了上述的难点。
p
=
1
1
+
e
?
w
x
T
+
b
p = \frac{1}{1+e^{-wx^T+b}}
p=1+e?wxT+b1?
其中x表示的是向量,我们可以有多个连续的数值进行输入,w也是与之对应的向量,我们需要优化计算的就是w。
提前计算好梯度的公式
实现的过程是比较简单的都是直接对公式进行复现,难点在🌧?梯度的计算。损失函数是用极大似然来计算的,这也是为什么用的是梯度上升算法。
l
o
s
s
(
w
)
=
∏
i
s
i
g
m
o
i
d
(
x
i
)
y
i
(
1
?
s
i
g
m
o
i
d
(
x
i
)
)
1
?
y
i
l
o
g
(
l
o
s
s
)
=
∑
i
(
y
i
?
s
i
g
m
o
i
d
(
x
i
)
+
(
1
?
y
i
)
?
l
o
g
(
1
?
s
i
g
m
o
i
d
(
x
i
)
)
)
l
o
g
(
l
o
s
s
)
=
∑
i
(
y
i
?
(
w
T
x
i
)
?
l
o
g
(
1
+
e
w
T
x
i
)
)
?
l
o
s
s
(
w
)
?
w
=
y
x
?
1
1
+
e
w
T
x
?
e
w
T
x
?
x
=
x
(
y
?
s
i
g
m
o
i
d
(
x
)
)
loss(w) = \prod_isigmoid(x_i)^{y_i}(1-sigmoid(x_i))^{1-y_i} \\ log(loss)=\sum_i(y_i*sigmoid(x_i)+(1-y_i)*log(1-sigmoid(x_i))) \\ log(loss)=\sum_i(y_i*(w^Tx_i)-log(1+e^{w^Tx_i})) \\ \frac{\partial loss(w)}{\partial w}= yx - \frac{1}{1+e^{w^Tx}}*e^{w^Tx}*x \\ =x(y-sigmoid(x))
loss(w)=i∏?sigmoid(xi?)yi?(1?sigmoid(xi?))1?yi?log(loss)=i∑?(yi??sigmoid(xi?)+(1?yi?)?log(1?sigmoid(xi?)))log(loss)=i∑?(yi??(wTxi?)?log(1+ewTxi?))?w?loss(w)?=yx?1+ewTx1??ewTx?x=x(y?sigmoid(x))
现在就万事俱备只欠东风了🚢
算法实现
和之前一样我们先导数据,(数据我会单独上传的testSet.txt)
def loadDataSet():
dataMat = []; LabelMat = []
fr = open('testSet.txt')
for line in fr.readlines():
linedata = line.strip().split()
dataMat.append([1.0,float(linedata[0]),float(linedata[1])])
LabelMat.append(int(linedata[2]))
return dataMat,LabelMat
x,y = loadDataSet()
然后定义好sigmoid和梯度上升就可以了
def sigmoid(x):
return 1/(1+np.exp(-x))
def AscengGrad(data, label):
data = np.mat(data)
label = np.mat(label).transpose()
m,n = data.shape
lr = 0.001
epoch = 500
weight = np.ones((n,1))
for i in range(epoch):
sigma = sigmoid(data*weight)
loss = label - sigma
weight = weight + lr * data.T * loss
return weight
AscengGrad(x,y)
当然这个算法也不是不可以改进的,改进的话可以考虑通过数据的大小,这里的想法就是用小批量进行训练和深度学习的batch训练思路一样,关于这部分内容以后会在深度学习内出现。