文章目录
1 - cora数据集
2 - 源码含义记录
首先我们来整体看一下代码的组成

截图中的这一大坨为命令行传递参数,含义参考命令行传递参数 argparse.ArgumentParser解析简单点说,就是想在不改动代码的情况下,使用命令行去改参数。
2.1 加载数据集
在代码中,加载数据集通过这个函数实现
# Load data
adj, features, labels, idx_train, idx_val, idx_test = load_data()
可以看看load_data中的内容:
def load_data(path="../data/cora/", dataset="cora"):
"""Load citation network dataset (cora only for now)"""
print('Loading {} dataset...'.format(dataset))
idx_features_labels = np.genfromtxt("{}{}.content".format(path, dataset),
dtype=np.dtype(str))
features = sp.csr_matrix(idx_features_labels[:, 1:-1], dtype=np.float32) # 取特征feature
labels = encode_onehot(idx_features_labels[:, -1]) # one-hot label
# build graph
idx = np.array(idx_features_labels[:, 0], dtype=np.int32) # 节点
idx_map = {j: i for i, j in enumerate(idx)} # 构建节点的索引字典
edges_unordered = np.genfromtxt("{}{}.cites".format(path, dataset),
dtype=np.int32) # 导入edge的数据
edges = np.array(list(map(idx_map.get, edges_unordered.flatten())),
dtype=np.int32).reshape(edges_unordered.shape) # 将之前的转换成字典编号后的边
adj = sp.coo_matrix((np.ones(edges.shape[0]), (edges[:, 0], edges[:, 1])),
shape=(labels.shape[0], labels.shape[0]),
dtype=np.float32) # 构造邻接矩阵
# build symmetric adjacency matrix 计算邻接矩阵的对称矩阵,因为cora是有向图,而GCN是无向图
adj = adj + adj.T.multiply(adj.T > adj) - adj.multiply(adj.T > adj)
features = normalize(features)
adj = normalize(adj + sp.eye(adj.shape[0]))
idx_train = range(140)
idx_val = range(200, 500)
idx_test = range(500, 1500)
features = torch.FloatTensor(np.array(features.todense()))
labels = torch.LongTensor(np.where(labels)[1])
adj = sparse_mx_to_torch_sparse_tensor(adj)
idx_train = torch.LongTensor(idx_train)
idx_val = torch.LongTensor(idx_val)
idx_test = torch.LongTensor(idx_test)
return adj, features, labels, idx_train, idx_val, idx_test
np.genfromtxt函数为numpy加载数据集,当然还有其它几种加载数据集的方式,例如pandas等等,详情见Python加载数据的5种不同方式(收藏)。
2.1.1 加载节点数据
首先是加载节点的数据,即.content。
通过断点+命令行调试,可以看到输出的idx_features_labels的结果

因此我们想把中间节点的特征给取出来,即这一句
features = sp.csr_matrix(idx_features_labels[:, 1:-1], dtype=np.float32)
中间[1:-1]是从第二列到倒数第二列(因为python为左闭右开)
然后再取label,使用
labels = encode_onehot(idx_features_labels[:, -1])
只取最后一列,并且采用one-hot编码。
分别看看上述两行代码的输出
解释一下特征的含义

最后开始取节点的索引(index),即第一列,并且构建节点的索引字典。
idx = np.array(idx_features_labels[:, 0], dtype=np.int32) # 取节点
idx_map = {j: i for i, j in enumerate(idx)} # 构建节点的索引字典
看看输出,字典就构建好啦
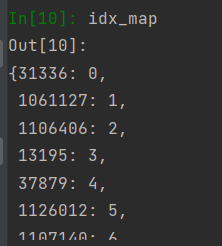
2.1.2 加载边的数据
节点的数据导入完了,我们再来导入边的数据
edges_unordered = np.genfromtxt("{}{}.cites".format(path, dataset), dtype=np.int32) # 导入edge的数据

将之前的转换成字典编号后的边
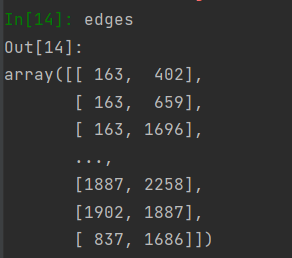
2.1.3 构造邻接矩阵
adj = sp.coo_matrix((np.ones(edges.shape[0]), (edges[:, 0], edges[:, 1])),
shape=(labels.shape[0], labels.shape[0]),
dtype=np.float32) # 构造边的邻接矩阵(稀疏矩阵)
看看邻接矩阵的大小和样子,因为有2708个节点,所以大小为(2708×2708)

由于Cora数据集是一个有向图,而GCN本身使用的为无向图,其邻接矩阵是对称的,因此我们需要构造一个对称矩阵,如下:
# build symmetric adjacency matrix 计算邻接矩阵的对称矩阵,因为cora是有向图,而GCN是无向图
adj = adj + adj.T.multiply(adj.T > adj) - adj.multiply(adj.T > adj)
其中adj.T > adj的含义为,如果转置后为1,而原矩阵为0,则该位置为1
Python将非对称邻接矩阵转变为对称邻接矩阵(有向图转无向图)
2.1.4 归一化
features = normalize(features)
adj = normalize(adj + sp.eye(adj.shape[0]))
我们可以看一下normalize函数
def normalize(mx):
"""Row-normalize sparse matrix"""
rowsum = np.array(mx.sum(1)) # 矩阵行求和
r_inv = np.power(rowsum, -1).flatten() # 求和的-1次方,即倒数
r_inv[np.isinf(r_inv)] = 0. # 求倒数的时候有可能是无穷,因此如果是无穷的话,就转换成0
r_mat_inv = sp.diags(r_inv) # 构造对角矩阵
mx = r_mat_inv.dot(mx) # 构造D-1 * A,特征归一化,非对称方式,简化方式
return mx
分别看看rowsum和r_inv的输出

然后我们在把r_inv中的无穷值变为0后,构造对角矩阵,可以看到结果

特征矩阵归一化(非必须)
做了上述这些后,我们对特征矩阵进行归一化
可以发现特征每一行加起来都是1,已经被归一化好了。
邻接矩阵归一化(必须)
再对邻接矩阵+单位阵进行归一化(必须操作)

首先看起来邻接矩阵+单位阵的值:

然后再进行归一化,这里用的是简便方法,和上面一样啦~
2.1.5 加载数据集/数据格式转换
# 训练、验证、测试的样本
idx_train = range(140)
idx_val = range(200, 500)
idx_test = range(500, 1500)
# 将numpy的数据转换成torch格式
features = torch.FloatTensor(np.array(features.todense()))
labels = torch.LongTensor(np.where(labels)[1])
adj = sparse_mx_to_torch_sparse_tensor(adj)
idx_train = torch.LongTensor(idx_train)
idx_val = torch.LongTensor(idx_val)
最后返回的格式
return adj, features, labels, idx_train, idx_val, idx_test
2.2 构造模型
我们构造一个GCN模型和优化器
# Model and optimizer 构造GCN,初始化参数,两层GCN
model = GCN(nfeat=features.shape[1],
nhid=args.hidden,
nclass=labels.max().item() + 1,
dropout=args.dropout)
optimizer = optim.Adam(model.parameters(),
lr=args.lr, weight_decay=args.weight_decay)
当然想看看GCN长什么样啦~
class GCN(nn.Module):
def __init__(self, nfeat, nhid, nclass, dropout):
super(GCN, self).__init__()
self.gc1 = GraphConvolution(nfeat, nhid) # 构建第一层GCN
self.gc2 = GraphConvolution(nhid, nclass) # 构建第二层GCN
self.dropout = dropout
def forward(self, x, adj):
x = F.relu(self.gc1(x, adj))
x = F.dropout(x, self.dropout, training=self.training)
x = self.gc2(x, adj)
return F.log_softmax(x, dim=1)
在初始化里,看到了GraphConvolution函数,自然想看看它是什么样子的
class GraphConvolution(Module):
"""
Simple GCN layer, similar to https://arxiv.org/abs/1609.02907
"""
def __init__(self, in_features, out_features, bias=True):
super(GraphConvolution, self).__init__()
self.in_features = in_features
self.out_features = out_features
self.weight = Parameter(torch.FloatTensor(in_features, out_features)) # 参数化,变成可以训练的
if bias:
self.bias = Parameter(torch.FloatTensor(out_features))
else:
self.register_parameter('bias', None)
self.reset_parameters()
def reset_parameters(self): # 参数随机化
stdv = 1. / math.sqrt(self.weight.size(1))
self.weight.data.uniform_(-stdv, stdv)
if self.bias is not None:
self.bias.data.uniform_(-stdv, stdv)
def forward(self, input, adj):
support = torch.mm(input, self.weight) # 输入和权重矩阵进行相乘
output = torch.spmm(adj, support) # 邻接矩阵和上面的结果相乘,spmm是稀疏矩阵的相乘
if self.bias is not None:
return output + self.bias
else:
return output
def __repr__(self):
return self.__class__.__name__ + ' (' \
+ str(self.in_features) + ' -> ' \
+ str(self.out_features) + ')'
这里的forward函数就是矩阵的相乘

2.3 使用GPU
if args.cuda:
model.cuda()
features = features.cuda()
adj = adj.cuda()
labels = labels.cuda()
idx_train = idx_train.cuda()
idx_val = idx_val.cuda()
idx_test = idx_test.cuda()
2.4 定义训练和测试函数
def train(epoch):
t = time.time()
model.train()
optimizer.zero_grad()
output = model(features, adj)
loss_train = F.nll_loss(output[idx_train], labels[idx_train])
acc_train = accuracy(output[idx_train], labels[idx_train])
loss_train.backward()
optimizer.step()
if not args.fastmode:
# Evaluate validation set performance separately,
# deactivates dropout during validation run.
model.eval()
output = model(features, adj)
loss_val = F.nll_loss(output[idx_val], labels[idx_val])
acc_val = accuracy(output[idx_val], labels[idx_val])
print('Epoch: {:04d}'.format(epoch+1),
'loss_train: {:.4f}'.format(loss_train.item()),
'acc_train: {:.4f}'.format(acc_train.item()),
'loss_val: {:.4f}'.format(loss_val.item()),
'acc_val: {:.4f}'.format(acc_val.item()),
'time: {:.4f}s'.format(time.time() - t))
def test():
model.eval()
output = model(features, adj)
loss_test = F.nll_loss(output[idx_test], labels[idx_test])
acc_test = accuracy(output[idx_test], labels[idx_test])
print("Test set results:",
"loss= {:.4f}".format(loss_test.item()),
"accuracy= {:.4f}".format(acc_test.item()))
2.5 模型训练和测试
# Train model
t_total = time.time()
for epoch in range(args.epochs):
train(epoch)
print("Optimization Finished!")
print("Total time elapsed: {:.4f}s".format(time.time() - t_total))
# Testing
test()
首先我们看一下模型第一层输出的size

经过一个dropout,再经过第二层gcn,此时的input已经是

第二层要学习的权重,维度为

学完之后,x变为

最后经过一个log_softmax,得到output

训练完之后计算loss,然后计算准确度(不是很重要)
def accuracy(output, labels):
preds = output.max(1)[1].type_as(labels) # 输出哪个是最大的,即相应类别
correct = preds.eq(labels).double()
correct = correct.sum()
return correct / len(labels)
训练完了再测试,就大功告成啦