[人工智能]python 皮尔森相关系数（Pearson）

一、概述

• 皮尔森相关系数也称皮尔森积矩相关系数(Pearson product-moment correlation coefficient) ，是一种线性相关系数，是最常用的一种相关系数。记为r，用来反映两个变量X和Y的线性相关程度，r 值介于-1到1之间，绝对值越大表明相关性越强。
• 适用连续变量。
• 相关系数与相关程度一般划分为
  ?? 0.8 - 1.0 极强相关
  ?? 0.6 - 0.8 强相关
  ?? 0.4 - 0.6 中等程度相关
  ?? 0.2 - 0.4 弱相关
  ?? 0.0 - 0.2 极弱相关或无相关

二、定义

2.1 总体样本定义

$$\begin{array}{r}{\rho }_{X,Y}=\frac{cov(X,Y)}{{\sigma }_X{\sigma }_Y}=\frac{E(X?{\mu }_X)E(Y?{\mu }_Y)}{{\sigma }_X{\sigma }_Y}\end{array}$$
其中， σ X = E { [ X ? E ( X ) ] 2 } , σ Y = E { [ Y ? E ( Y ) ] 2 } \sigma_{X} = \sqrt{E\{[X - E(X)]^{2}\}},\sigma_{Y} = \sqrt{E\{[Y - E(Y)]^{2}\}} σX?=E{[X?E(X)]2} ?,σY?=E{[Y?E(Y)]2} ?

2.2 估算样本定义

• 估算样本的协方差和标准差，可得到样本相关系数（即样本皮尔森相关系数），常用 r 表示：
  $$\begin{array}{r}r=\frac{\sum _{i=1}^n(X_i?\overline{X})(Y_i?\overline{Y})}{\sqrt{\sum _{i=1}^n(X_i?\overline{X}{)}^2}\sqrt{\sum _{i=1}^n(Y_i?\overline{Y}{)}^2}}\end{array}$$

• 还可以由(Xi,Yi)样本点的标准分数均值估计得到与上式等价的表达式
  $$\begin{array}{r}r=\frac{1}{n?1}\sum _{i=1}^n(\frac{X_i?\overline{X}}{{\sigma }_X})(\frac{Y_i?\overline{Y}}{{\sigma }_Y})\end{array}$$
  其中，$\frac{X_i?\overline{X}}{{\sigma }_X}$ 是样本X的标准分数。

2.3 两种计算方式

• (1)
  $$\begin{array}{r}{\rho }_{X,Y}=\frac{cov(X,Y)}{{\sigma }_X{\sigma }_Y}=\frac{E(X?{\mu }_X)E(Y?{\mu }_Y)}{{\sigma }_X{\sigma }_Y}=\frac{E(XY)?E(X)E(Y)}{\sqrt{E(X^2)?E^2(X)}\sqrt{E(Y^2)?E^2(Y)}}\end{array}$$

• (2)
  $$\begin{array}{r}{\rho }_{X,Y}=\frac{n\sum XY?\sum X\sum Y}{\sqrt{n\sum X^2?(\sum X{)}^2}\sqrt{n\sum Y^2?(\sum Y{)}^2}}\end{array}$$

2.4 皮尔森距离

$$d_{X,Y}=1?{\rho }_{X,Y}$$

三、python 实现

3.1 生成随机数据集

import random
import pandas as pd

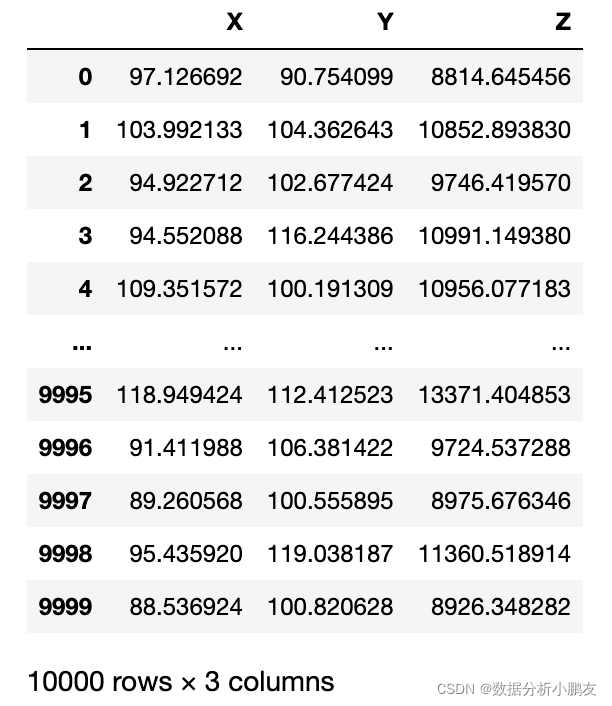
n = 10000
X = [random.normalvariate(100, 10) for i in range(n)] # 随机生成服从均值100，标准差10的正态分布序列
Y = [random.normalvariate(100, 10) for i in range(n)] # 随机生成服从均值100，标准差10的正态分布序列
Z = [i*j for i,j in zip(X,Y)]
df = pd.DataFrame({"X":X,"Y":Y,"Z":Z})

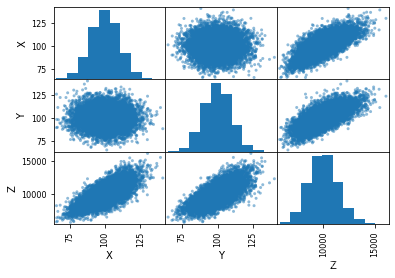
3.2 绘制散点图

import matplotlib.pyplot as plt 

# 绘制散点图矩阵
pd.plotting.scatter_matrix(df)
plt.show()

3.3 计算相关系数

3.3.1 自定义函数（无显著性检验）

import math

def PearsonFirst(X,Y):
    '''
        公式一
    '''
    XY = X*Y
    EX = X.mean()
    EY = Y.mean()
    EX2 = (X**2).mean()
    EY2 = (Y**2).mean()
    EXY = XY.mean()
    numerator = EXY - EX*EY                                 # 分子
    denominator = math.sqrt(EX2-EX**2)*math.sqrt(EY2-EY**2) # 分母
    
    if denominator == 0:
        return 'NaN'
    rhoXY = numerator/denominator
    return rhoXY

def PearsonSecond(X,Y):
    '''
        公式二
    '''
    XY = X*Y
    X2 = X**2
    Y2 = Y**2
    n = len(XY)
    numerator = n*XY.sum() - X.sum()*Y.sum()                                            # 分子
    denominator = math.sqrt(n*X2.sum() - X.sum()**2)*math.sqrt(n*Y2.sum() - Y.sum()**2) # 分母
    
    if denominator == 0:
        return 'NaN'
    rhoXY = numerator/denominator
    return rhoXY 
    
r1 = PearsonFirst(df['X'],df['Z'])  # 使用公式一计算X与Z的相关系数
r2 = PearsonSecond(df['X'],df['Z']) # 使用公式二计算X与Z的相关系数
print("r1: ",r1)
print("r2: ",r2)

3.3.2 python 函数

（1）pandas.corr 函数（无显著性检验）

• 参数解析
  DataFrame.corr(
  ??method = ‘pearson’, # 可选值为{‘pearson’:‘皮尔森’, ‘kendall’:‘肯德尔秩相关’, ‘spearman’:‘斯皮尔曼’}
  ??min_periods=1 ?? # 样本最少的数据量
  )

df.corr(method="pearson")

（2）scipy.stats.pearsonr 函数 （有显著性检验）

from scipy.stats import pearsonr

r = pearsonr(df['X'],df['Z'])
print("pearson系数：",r[0])
print("   P-Value：",r[1])

（3）pandas.corr 加 scipy.stats.pearsonr 获取相关系数检验P值矩阵

def GetPvalue_Pearson(x,y):
    return pearsonr(x,y)[1]

df.corr(method=GetPvalue_Pearson)

• 参考：pandas.DataFrame.corr
• 参考：皮尔森相关系数(Pearson correlation coefficient)
• 参考：scipy.stats.pearson