文章目录
1. 分类问题模型性能评价指标
当我们用机器学习或深度学习算法做分类问题时,必不可免要设计到一个问题:如何评价这些算法的性能?
回答这个问题,需要我们了解分类问题模型性能评价的相关指标。
常用的指标有:准确率(accucary)、精确率(precision)、召回率(recall)、灵敏度(sensitive)、特效度(sensitive)、F-Score、Micro-F1、Macro-F1、P-R曲线、ROC曲线和AUC等。

2. 混淆矩阵(confusion matrix)
上图中的各种指标,都是建立在一个基础之上:混淆矩阵(confusion matrix)。
表1 二分类问题的混淆矩阵
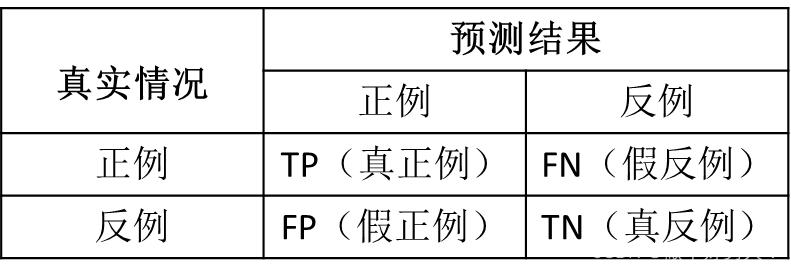
表2 中英文对照表
| 中文 | 英文全拼 | 英文缩写 |
|---|---|---|
| 正例 | Positive | P |
| 反例 | Negative | N |
| 真正例/真阳性 | Ture Positive | TP |
| 假正例/假阳性 | False Positive | FP |
| 假反例/假阴性 | False Negative | FN |
| 真反例/真阴性 | Ture Negative | TN |
基本等式:
全部样本 = TP + FP + FN + TN
P表示分类器判定为正样本 P = TP + FP
N表示分类器判定为负样本N = FN + TN
全部样本 = P + N
对于二分类问题,混淆矩阵是2x2 ,对于n分类问题,混淆矩阵是nxn的。混淆矩阵是用来记录分类器的预测结果的,根据混淆矩阵可以计算出各种指标。
怎么机器学习中正例和反例的概念呢?
笔者举个例子:
- 一个二分类问题,现有500幅动物图片(100幅为猫的图片),现把猫的图片当作“正例”,则非猫的图片就是“反例”。同时因为正例少,反例多,我们可以说这个数据是不均衡的。
- 现有一个分类器,拿出一个图片,让这个分类器做预测。如果这个图片实际为猫,分类器预测为猫,则为真正例,混肴矩阵中TP的值+1;
- 如果如果这个图片实际为猫,分类器预测非猫,则为假正例,混肴矩阵中FN的值+1;
- 如果这个图片实际为狗,分类器预测为猫,则为假反例,混肴矩阵中FP的值+1;
- 如果这个图片实际为狗,分类器预测为狗,则为真反例,混肴矩阵中TN的值+1;
3. 准确率(accucary)、精确率(precision)、召回率(recall)
准确率(accucary):是被正确分类的样本占所有样本数的比例;对分类器整体分类正确率性能的评价。1-accucary = error rate

精确率(precision):预测为正例的样本中,有多少是真正例。预测为某类的样本中,有多少真的是这一类。 又叫查准率。
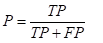
召回率(recall):预测正确的样本中,占实际样本的比例。正确预测为某类的样本,占实际该类样本量的比例。 又叫查全率。对应工业检测上的漏检率。漏检率= 1- Recall (工业上的缺陷检测,希望应检尽检,缺陷漏检率为0)
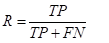
4. 灵敏度(sensitive)、特效度(sensitive)
灵敏度(sensitive):所有正例中被分对的比例,衡量了分类器对正例的识别能力
灵敏度(sensitive)其实就是精确率(precision),一般在医学上使用灵敏度这个概念。
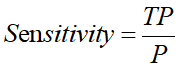
特效度(sensitive):所有负例中被分对的比例,衡量了分类器对负例的识别能力
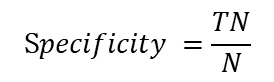
5. F-Score / F-Measure
从精确率和召回率的定义和概念,我们可以看出,这是一对矛盾的指标。一般来说,在复杂任务中,使精确率和召回率都很好,是比较难的。
P和R指标有时候会出现矛盾,这样就要综合考虑他们,最常见的方法就是F-Score(又称为F-Measure)
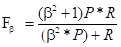
从公式可以看出,F是P和R的加权平均。当beta取1时,F-Score被称为 F1-Score
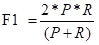
6. Macro-F1 和 Micro-F1
很多时候,我们有多个二分类混淆矩阵,例如:进行多次训练/测试,每次得到一个混淆矩阵。我们希望在这n个混淆矩阵上,综合考察精确率和召回率。
一种常见的做法是:对P相加后求平均,得到 Macro-P;对R相加后求平均,得到 Macro-R;最后将Macro-P和Macro-R代入F1公式。
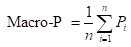
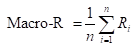
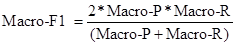
还可以将各混淆矩阵对应元素进行平均,得到:
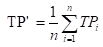
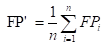
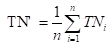
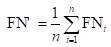
再基于这些,计算出微精确率Micro-P和微召回率Micro-R
在基于Micro-P和Micro-R,得出微F1(Micro-F1)
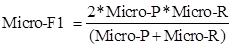
7. P-R曲线、ROC曲线和AUC
等待以后补充……
8. 代码实现(python)
metrics.py
# %%
import torch
import numpy as np
import os
class Metrics:
def __init__(self, pred:torch.Tensor, true:torch.Tensor, n_class):
assert pred.shape[0] == true.shape[0]
assert pred.shape[1] == n_class
pred, true = pred.detach(), true.detach()
# target is (batch_size, ...)
pred = torch.argmax(pred, dim=1).flatten()
true = true.flatten()
mask = (true >= 0) & (true < n_class)
self.true = true[mask]
self.pred = pred[mask]
self.n_class = n_class
def confusion_matrix(self):
if not hasattr(self, 'cm'):
indices = self.n_class * self.true + self.pred
self.cm = torch.bincount(indices, minlength=self.n_class ** 2).reshape(self.n_class, self.n_class)
self.cm = self.cm.float()
return self.cm
def accuracy_score(self):
if not hasattr(self, 'acc'):
count = torch.sum(torch.eq(self.true, self.pred), dtype=torch.float32)
self.acc = count/self.true.shape[0]
return self.acc
def precision_score(self):
if not hasattr(self, 'pr'):
self.pr = torch.sum(self.confusion_matrix(), dim=0)
for i in range(self.n_class):
self.pr[i] = self.confusion_matrix()[i, i]/self.pr[i]
return self.pr
def recall_score(self):
if not hasattr(self, 're'):
self.re = torch.sum(self.confusion_matrix(), dim=1)
for i in range(self.n_class):
self.re[i] = self.confusion_matrix()[i, i]/self.re[i]
return self.re
def f1_score(self):
if not hasattr(self, 'f1'):
self.f1 = 2*self.precision_score()*self.recall_score() / (self.precision_score()+self.recall_score()+1e-5)
self.macro_f1 = torch.mean(self.f1)
return self.f1, self.macro_f1
def cohen_kappa_score(self):
if not hasattr(self, 'k'):
p0 = self.accuracy_score()
pe = torch.sum(torch.sum(self.confusion_matrix(), dim=0)*torch.sum(self.confusion_matrix(), dim=1))/(self.true.shape[0]**2)
self.k = (p0-pe)/(1-pe)
return self.k
def print_metrics(self):
cm = self.confusion_matrix().cpu().int().detach().numpy()
print('confusion_matrix:')
print(cm)
print('precision:')
print(np.round(self.precision_score().cpu().detach().numpy()*100, 2))
print('recall:')
print(np.round(self.recall_score().cpu().detach().numpy()*100, 2))
f1, mf1 = self.f1_score()
print('f1:')
print(np.round(f1.cpu().detach().numpy()*100, 2))
print('acc:')
print(np.round(self.accuracy_score().item()*100, 2))
print('mf1:')
print(np.round(mf1.item()*100, 2))
print('k:')
print(np.round(self.cohen_kappa_score().item(), 3))
def save_metrics(self, save_path):
from openpyxl import Workbook
wb = Workbook()
ws = wb.active
ws.merge_cells('A1:A2')
ws.merge_cells('B1:F1')
ws.merge_cells('G1:J1')
ws.merge_cells('J3:J7')
ws.cell(1, 2, 'Predictions')
ws.cell(1, 7, 'Metrics')
for i, s in enumerate(['W', 'N1', 'N2', 'N3', 'R', 'PR', 'RE', 'F1', 'Overall']):
ws.cell(2, i+2, s)
for i, s in enumerate(['W', 'N1', 'N2', 'N3', 'R']):
ws.cell(i+3, 1, s)
for i in range(5):
for j in range(5):
ws.cell(i+3, j+2, int(self.confusion_matrix()[i, j].item()))
for i, pr in enumerate(self.precision_score()):
ws.cell(i+3, 7, np.round(pr.item()*100, 2))
for i, re in enumerate(self.recall_score()):
ws.cell(i+3, 8, np.round(re.item()*100, 2))
f1, mf1 = self.f1_score()
for i, _f1 in enumerate(f1):
ws.cell(i+3, 9, np.round(_f1.item()*100, 2))
acc = np.round(self.accuracy_score().item()*100, 2)
mf1 = np.round(mf1.item()*100, 2)
kappa = np.round(self.cohen_kappa_score().item(), 3)
val = f'ACC: {acc}\r\nMF1: {mf1}\r\nKappa: {kappa}\r\nTime: '
ws.cell(3, 10, val)
wb.save(os.path.join(save_path, 'metrics.xlsx'))
Metrics类提供记录混淆矩阵的方法,提供计算Precision、Recall、F1-Score等的方法。