Def
- 损失函数loss:对单个样本
- 代价函数cost:对整个训练集 MSE均方误差
- 梯度(Batch gradient):cost对权重的导数
- 随机梯度(Stochastic gradient):loss对权重的导数
- 凸函数:任取两个点,画一条直线,直线都在曲线上方,则为凸函数。凸函数有全局最优。
- BGD:收敛到局部最优
- SGD:更容易收敛到全局最优,但时间复杂度大
- GD 和 SGD 的折中:mini-batchGD (深度学习中常用)
- 鞍点:导数那里等于零(某段曲线斜率为0,平了)
代码分析

02-BGD
# -*- coding:utf-8 -*-
# Abstract : 模型:y^ = wx BGD
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = 1.0
def forward(x):
return w * x
def cost(xs, ys):
cost = 0.0
for x,y in zip(xs, ys):
y_pred = forward(x)
loss = (y_pred - y) ** 2
cost += loss
return cost/len(xs)
def gradient(xs,ys):
grad = 0.0
for x,y in zip(xs,ys):
y_pred = forward(x)
grad += 2 * x * (y_pred - y)
return grad/len(xs)
def draw():
plt.plot(ep_lst,cost_lst)
plt.xlabel('epoch')
plt.ylabel('cost')
plt.show()
cost_lst = []
ep_lst = []
learning_rate = 0.01
for epoch in range(0,101,1):
ep_lst.append(epoch)
cost_val = cost(x_data, y_data)
cost_lst.append(cost_val)
grad_val = gradient(x_data, y_data)
w = w - learning_rate * grad_val
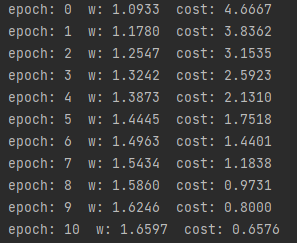
print('epoch:', epoch, ' w:', '%.4f'%w, ' cost:','%.4f'%cost_val)
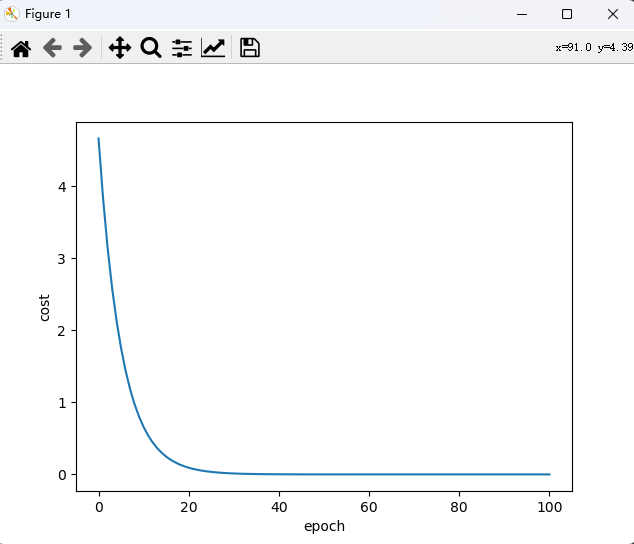
draw()
结果:
02-SGD
# -*- coding:utf-8 -*-
# Abstract : 模型:y^ = wx SGD
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = 1.0
def forward(x):
return w * x
def loss(x, y):
y_pred = forward(x)
loss = (y_pred - y) ** 2
return loss
def gradient(x,y):
y_pred = forward(x)
s_grad = 2 * x * (y_pred - y)
return s_grad
def draw():
plt.plot(ep_lst,loss_lst)
plt.xlabel('epoch')
plt.ylabel('cost')
plt.show()
loss_lst = []
ep_lst = []
learning_rate = 0.01
for epoch in range(0,101,1):
for x,y in zip(x_data, y_data):
ep_lst.append(epoch)
s_grad = gradient(x,y)
w = w - learning_rate * s_grad
loss_val = loss(x,y)
loss_lst.append(loss_val)
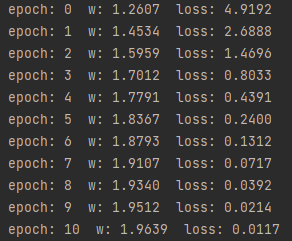
print('epoch:', epoch, ' w:', '%.4f'%w, ' loss:','%.4f'%loss_val)
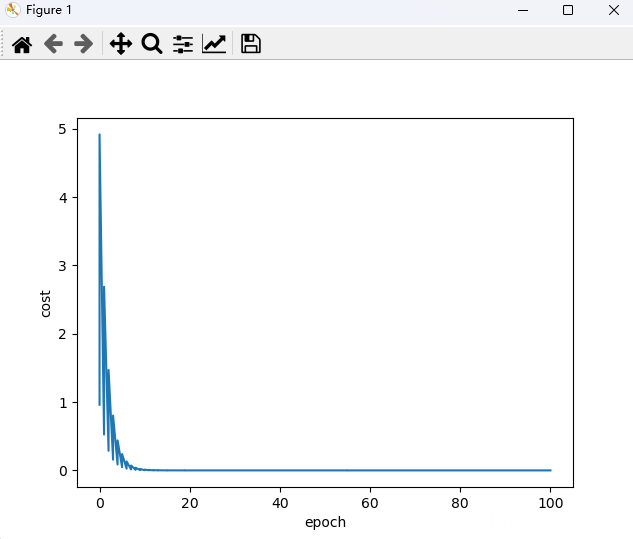
draw()
结果: