[人工智能]3.4 随机梯度下降【斯坦福21秋季：实用机器学习中文版】代码实现

题目

3.4 随机梯度下降【斯坦福21秋季：实用机器学习中文版】代码实现

代码

'''
Description: SGD代码实现
Autor: 365JHWZGo
Date: 2022-03-20 12:10:30
LastEditors: 365JHWZGo
LastEditTime: 2022-03-20 17:46:25
'''
import random
import torch
import matplotlib.pyplot as plt
EPOCH = 40
BATCH_SIZE = 32
m = 3
NUM = 1000
LR = 0.03

# 创造数据
def create_data(w, b, num_examples):
    # w.shape [m, 1]
    # b.shape [1]

    # X.shape [num_examples, m]
    X = torch.normal(0, 1, (num_examples, len(w)))

    # y = X*w = [num_examples, 1]
    y = torch.matmul(X, w) + b

    # Y.shape [num_examples, 1]
    Y = torch.normal(0, 0.01, y.shape)+y
    return X, Y

# batch数据截取
def data_iteration(batch_size, features, labels):
    # features.shape [num_examples, m]
    # labels.shape [num_examples, 1]

    num_examples = len(features)
    indices_num = list(range(num_examples))
    random.shuffle(indices_num)
    for i in range(0, num_examples, batch_size):
        data_indices = torch.tensor(
            # 当数据不足切片时，取到num_examples
            indices_num[i:min(i+batch_size, num_examples)]
        )
        # features.shape [batch_size, m]
        # labels.shape [batch_size, 1]
        yield features[data_indices], labels[data_indices]

# SGD函数
def SGD(y_acc, y_pre):
    loss = ((y_acc - y_pre)**2/2).sum()
    return loss

# 函数预测
def linear_predict(x, w, b):
    y = torch.matmul(x, w)+b
    return y


'''
实际上的w和b
'''
# w_acc.shape [m, 1]
w_acc = torch.tensor([[-2.0], [2.5], [-1.9]])
# b_acc.shape [1]
b_acc = torch.tensor([8.1])

# 生成有噪音的数据
features, labels = create_data(w_acc, b_acc, NUM)

'''
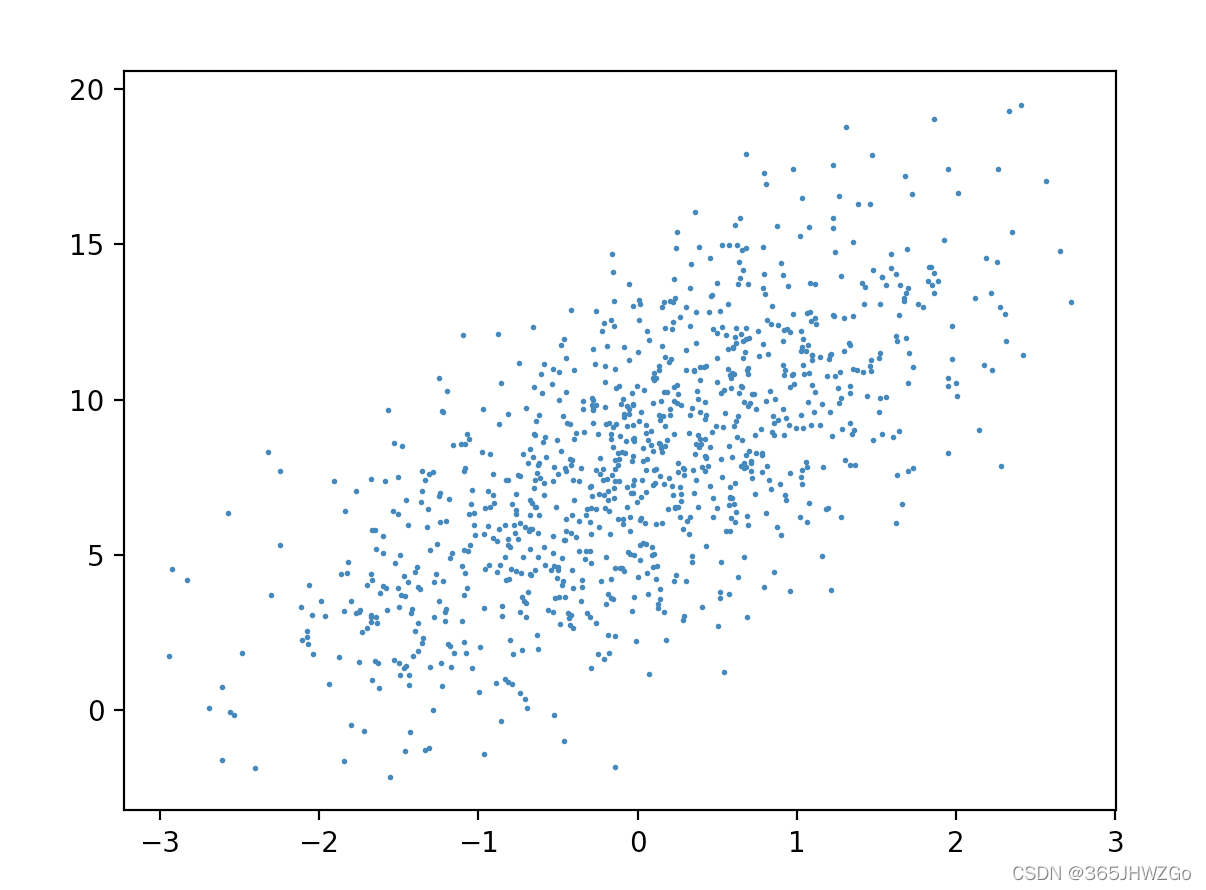
画图
plt.scatter(features[:, (1)].detach().numpy(), labels.detach().numpy(), 1)
plt.show()
'''

'''
预测时初始化w和b
'''
# w.shape [m, 1] 可导
w = torch.normal(0, 0.01, (m,1), requires_grad=True)
# b.shape [1] 可导
b = torch.zeros(1, requires_grad=True)

# 主函数入口
if __name__ == '__main__':
    
    for epoch in range(EPOCH):
        # features.shape [batch_size, m]
        # labels.shape [batch_size, 1]
        for f, l in data_iteration(BATCH_SIZE, features, labels):

            # 进行y值预测 y_pre.shape [batch_size, 1]
            y_pre = linear_predict(f, w, b)

            # SGD梯度下降
            loss = SGD(l, y_pre)

            # 求导
            loss.backward()

            with torch.no_grad():
                for param in [w, b]:
                    param -= LR * param.grad / BATCH_SIZE
                    param.grad.zero_()

        # test
        with torch.no_grad():
            test_loss = SGD(labels, linear_predict(features, w, b)).mean()
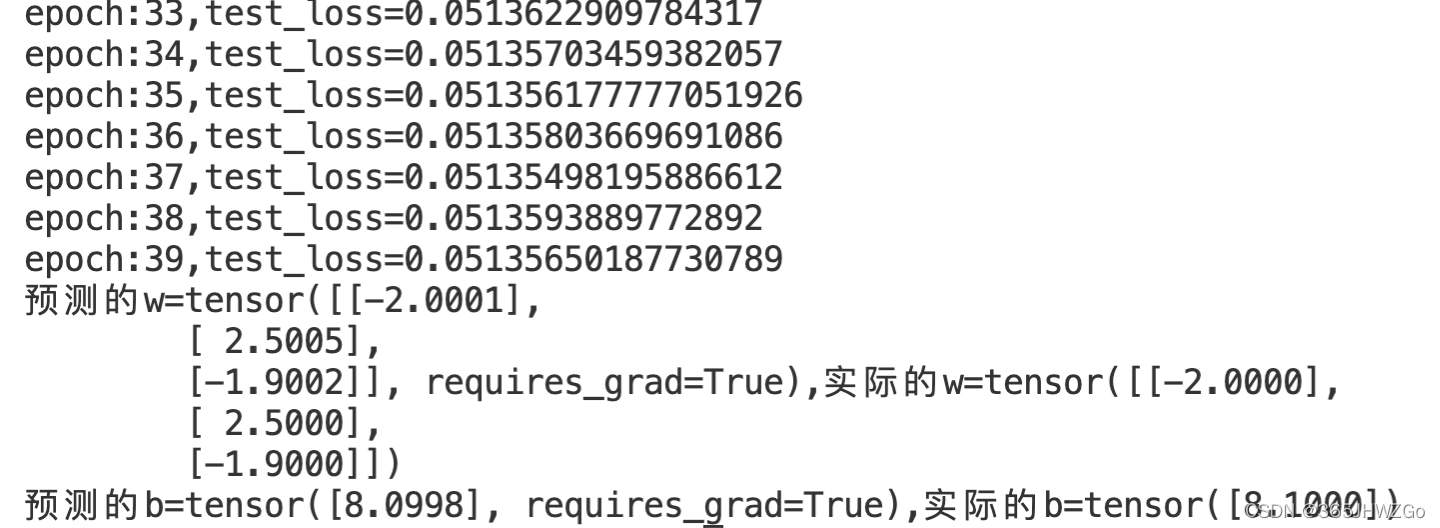
            print(f'epoch:{epoch},test_loss={test_loss}')
    print(f'预测的w={w},实际的w={w_acc}\n预测的b={b},实际的b={b_acc}')

'''
画图
'''
sample_x = np.linspace(-10,10,10)
w_accurancy = w_acc.flatten().numpy()
b_accurancy = b_acc.flatten().numpy()
sample_y = []
sample_y_pre = []
w_prediction = w.flatten().detach().numpy()
b_prediction = b.flatten().detach().numpy()
for i in range(len(sample_x)):
    sample_y.append(sample_x[i]*w_accurancy[0]+sample_x[i]*w_accurancy[1]+sample_x[i]*w_accurancy[2]+b_accurancy[0])
    sample_y_pre.append(sample_x[i]*w_prediction[0]+sample_x[i]*w_prediction[1]+sample_x[i]*w_prediction[2]+b_prediction[0])
plt.figure(num=0, figsize=(8, 5))
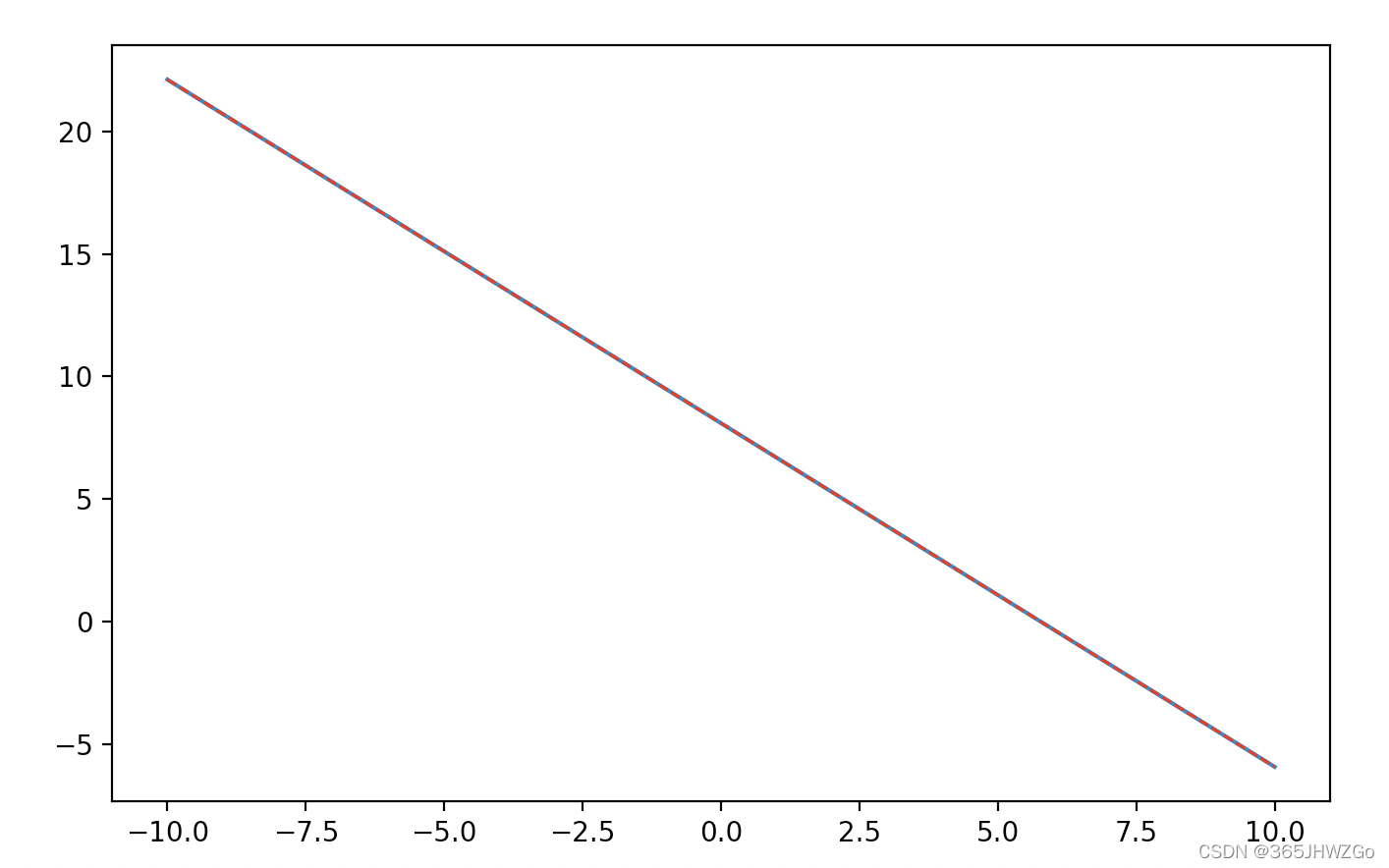
plt.plot(sample_x,sample_y,label="真实函数")
plt.plot(sample_x,sample_y_pre,color='red', linewidth=1.0, linestyle='--',label="预测函数")
plt.show()

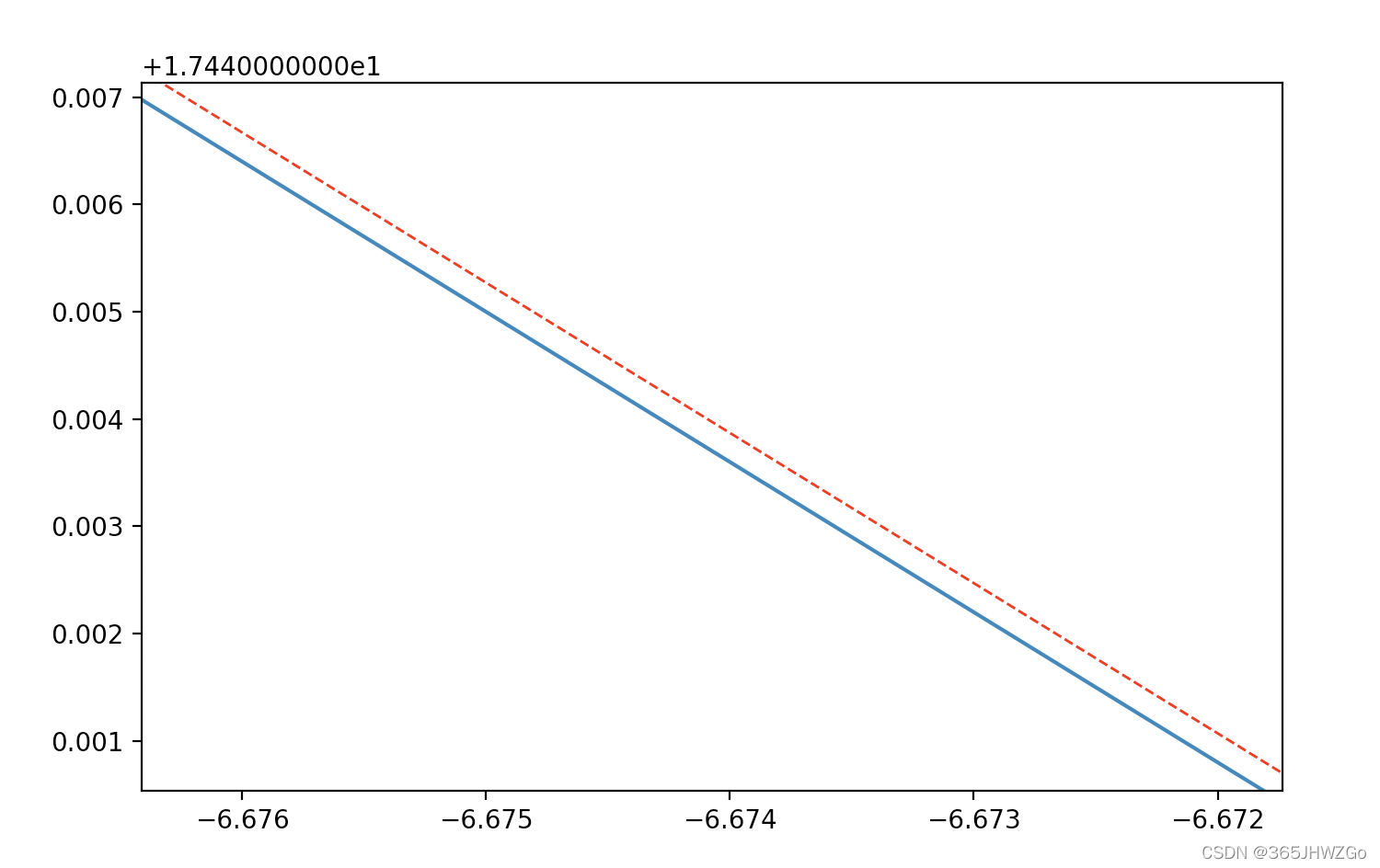
真实函数和预测函数比较

放大后