? ? ? 之前在https://blog.csdn.net/fengbingchun/article/details/75351323 介绍过梯度下降,常见的梯度下降有三种形式:BGD、SGD、MBGD,它们的不同之处在于我们使用多少数据来计算目标函数的梯度。
? ? ? 大多数深度学习算法都涉及某种形式的优化。优化指的是改变x以最小化或最大化某个函数f(x)的任务。我们通常以最小化f(x)指代大多数最优化问题。我们把要最小化或最大化的函数称为目标函数(objective function)或准则(criterion)。当我们对其进行最小化时,我们也把它称为成本函数(cost function)、损失函数(loss function)或误差函数(error function)。
? ? ? 梯度下降是深度学习中一种常用的优化技术。梯度是函数的斜率。它衡量一个变量响应另一个变量的变化而变化的程度。在数学上,梯度下降是一个凸函数,其输出是输入的一组参数的偏导数。梯度越大,坡度越陡(the greater the gradient, the steeper the slope)。从初始值开始,迭代运行梯度下降以找到参数的最佳值,以找到给定成本函数的最小可能值。
? ? ? 梯度下降是一种优化算法,通常用于寻找深度学习算法中的权值及系数(weights or coefficients),如逻辑回归。它的工作原理是让模型对训练数据进行预测,并使用预测中的error来更新模型从而减少error(It works by having the model make predictions on training data and using the error on the predictions to update the model in such a way as to reduce the error)。
? ? ? 该算法的目标是找到使模型在训练数据集上的误差最小化的模型参数(e.g. coefficients or weights)。它通过对模型进行更改,使其沿着误差的梯度或斜率向下移动到最小误差值来实现这一点。这使该算法获得了"梯度下降"的名称。
? ? ? 梯度下降是深度学习中非常流行的优化算法。它的目标是搜索目标函数或成本函数(objective function or cost function)的全局最小值。这只有在目标函数是凸函数时才有可能,这间接意味着该函数将是碗形的。在非凸函数的情况下,梯度下降会找到最近的最小值,这个函数的最小值称为局部最小值。
? ? ? 梯度下降是一种一阶优化算法。这意味着在更新参数时它只考虑函数的一阶导数。我们的主要目标是在每次迭代中使梯度沿最陡斜率的方向行进,我们在与目标函数的梯度相反的方向上更新参数。
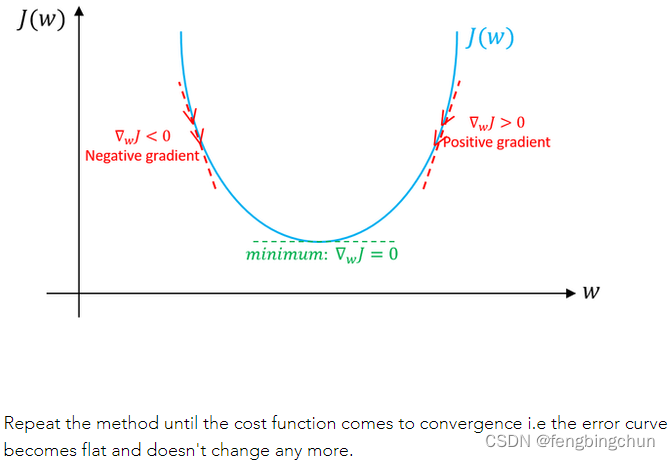
? ? ? 图解说明:假设只有weight没有bias。如果weight(w)的特定值的斜率>0,则表示我们在最优w*的右侧,在这种情况下,更新将是负数,并且w将开始接近最优w*。但是,如果weight(w)的特定值的斜率<0,则更新将为正值,并将当前值增加到w以收敛到w*的最佳值。以下截图来自于https://www.machinelearningman.com:重复该方法,直到成本函数收敛。
?? ? ? 在https://blog.csdn.net/fengbingchun/article/details/79370310 中有梯度下降应用于二分类的公式推导。
? ? ? BGD(Batch Gradient Descent):批量梯度下降,是梯度下降法最原始的形式,它计算训练数据集中每个样本的误差(error),使用所有的样本来进行参数更新。整个训练数据集的一个周期(one cycle)称为一个训练epoch。BGD是在每个训练epoch结束时才进行模型更新。
? ? ? 梯度下降是一种最小化目标函数的方法:θ为模型的参数,J(θ)为目标函数,以下截图来自https://arxiv.org/pdf/1609.04747.pdf?
 ???????
???????
?
? ? ? 批量梯度下降可以使用固定的学习率。同时处理整个训练集,只有处理完整个训练集才更新一次权值和偏置。
? ? ? 优点:
? ? ? (1).对模型的更新较小意味着这种形式的梯度下降比随机梯度下降的计算效率更高。
? ? ? (2).降低的(decreased)的更新频率会产生更稳定的误差梯度(error gradient),在某些问题上可能产生更稳定的收敛。
? ? ? (3).预测误差(prediction error)的计算和模型更新的分离使算法适用于基于并行处理的实现。
? ? ? 缺点:
? ? ? (1).更稳定的误差梯度可能会导致模型过早收敛到一组不太理想的参数。
? ? ? (2).训练结束时的更新需要在所有训练样本中累积预测误差的额外复杂性(additional complexity)。
? ? ? (3).通常需要将整个训练数据集加载到内存中以供算法使用。
? ? ? (4).对于大型数据集,模型更新以及训练速度可能会变得非常慢。
? ? ? 以上内容主要参考:
? ? ? 1. https://arxiv.org/pdf/1609.04747.pdf
? ? ? 2.?https://machinelearningmastery.com/
? ? ? 3. https://www.machinelearningman.com
? ? ? 以下的测试代码以https://blog.csdn.net/fengbingchun/article/details/79346691?中逻辑回归实现的基础上进行调整:
? ? ? logistic_regression2.hpp:
#ifndef FBC_SRC_NN_LOGISTIC_REGRESSION2_HPP_
#define FBC_SRC_NN_LOGISTIC_REGRESSION2_HPP_
#include <vector>
#include <string>
namespace ANN {
enum class ActivationFunction {
Sigmoid // logistic sigmoid function
};
enum class LossFunction {
MSE // Mean Square Error
};
enum class Optimzation {
BGD, // Batch_Gradient_Descent
SGD, // Stochastic Gradient Descent
MBGD // Mini-batch Gradient Descent
};
template<typename T>
class LogisticRegression2 { // two categories
public:
LogisticRegression2() = default;
int init(const T* data, const T* labels, int train_num, int feature_length, T learning_rate = 0.00001, int epochs = 300);
int train(const std::string& model);
int load_model(const std::string& model);
T predict(const T* data, int feature_length) const; // y = 1/(1+exp(-(wx+b)))
private:
int store_model(const std::string& model) const;
T calculate_z(const std::vector<T>& feature) const; // z(i)=w^T*x(i)+b
T calculate_cost_function() const;
T calculate_activation_function(T value) const;
T calculate_loss_function() const;
T calculate_loss_function_derivative() const;
T calculate_loss_function_derivative(unsigned int index) const;
void calculate_gradient_descent();
std::vector<std::vector<T>> x_; // training set
std::vector<T> y_; // ground truth labels
std::vector<T> o_; // predict value
int epochs_ = 100; // epochs
int m_ = 0; // train samples num
int feature_length_ = 0; // weights length
T alpha_ = (T)0.00001; // learning rate
std::vector<T> w_; // weights
T b_ = (T)0.; // threshold
ActivationFunction activation_func_ = ActivationFunction::Sigmoid;
LossFunction loss_func_ = LossFunction::MSE;
Optimzation optim_ = Optimzation::BGD;
}; // class LogisticRegression2
} // namespace ANN
#endif // FBC_SRC_NN_LOGISTIC_REGRESSION2_HPP_? ? ? logistic_regression2.cpp:
#include "logistic_regression2.hpp"
#include <fstream>
#include <algorithm>
#include <random>
#include <cmath>
#include "common.hpp"
namespace ANN {
template<typename T>
int LogisticRegression2<T>::init(const T* data, const T* labels, int train_num, int feature_length, T learning_rate, int epochs)
{
if (train_num < 2) {
fprintf(stderr, "logistic regression train samples num is too little: %d\n", train_num);
return -1;
}
if (learning_rate <= 0) {
fprintf(stderr, "learning rate must be greater 0: %f\n", learning_rate);
return -1;
}
if (epochs <= 0) {
fprintf(stderr, "number of epochs cannot be zero or a negative number: %d\n", epochs);
return -1;
}
alpha_ = learning_rate;
epochs_ = epochs;
m_ = train_num;
feature_length_ = feature_length;
x_.resize(m_);
y_.resize(m_);
o_.resize(m_);
for (int i = 0; i < m_; ++i) {
const T* p = data + i * feature_length_;
x_[i].resize(feature_length_);
for (int j = 0; j < feature_length_; ++j) {
x_[i][j] = p[j];
}
y_[i] = labels[i];
}
return 0;
}
template<typename T>
int LogisticRegression2<T>::train(const std::string& model)
{
CHECK(x_.size() == y_.size());
w_.resize(feature_length_, (T)0.);
generator_real_random_number(w_.data(), feature_length_, (T)-0.01f, (T)0.01f, true);
generator_real_random_number(&b_, 1, (T)-0.01f, (T)0.01f);
for (int iter = 0; iter < epochs_; ++iter) {
calculate_gradient_descent();
fprintf(stdout, "echoch: %d, cost function: %f\n", iter, calculate_cost_function());
}
CHECK(store_model(model) == 0);
return 0;
}
template<typename T>
int LogisticRegression2<T>::load_model(const std::string& model)
{
std::ifstream file;
file.open(model.c_str(), std::ios::binary);
if (!file.is_open()) {
fprintf(stderr, "open file fail: %s\n", model.c_str());
return -1;
}
int length{ 0 };
file.read((char*)&length, sizeof(length));
w_.resize(length);
feature_length_ = length;
file.read((char*)w_.data(), sizeof(T)*w_.size());
file.read((char*)&b_, sizeof(T));
file.close();
return 0;
}
template<typename T>
T LogisticRegression2<T>::predict(const T* data, int feature_length) const
{
CHECK(feature_length == feature_length_);
T value{ (T)0. };
for (int t = 0; t < feature_length_; ++t) {
value += data[t] * w_[t];
}
value += b_;
return (calculate_activation_function(value));
}
template<typename T>
int LogisticRegression2<T>::store_model(const std::string& model) const
{
std::ofstream file;
file.open(model.c_str(), std::ios::binary);
if (!file.is_open()) {
fprintf(stderr, "open file fail: %s\n", model.c_str());
return -1;
}
int length = w_.size();
file.write((char*)&length, sizeof(length));
file.write((char*)w_.data(), sizeof(T) * w_.size());
file.write((char*)&b_, sizeof(T));
file.close();
return 0;
}
template<typename T>
T LogisticRegression2<T>::calculate_z(const std::vector<T>& feature) const
{
T z{ 0. };
for (int i = 0; i < feature_length_; ++i) {
z += w_[i] * feature[i];
}
z += b_;
return z;
}
template<typename T>
T LogisticRegression2<T>::calculate_cost_function() const
{
/*// J+=-1/m([y(i)*loga(i)+(1-y(i))*log(1-a(i))])
// Note: log0 is not defined
T J{0.};
for (int i = 0; i < m_; ++i)
J += -(y_[i] * std::log(o_[i]) + (1 - y_[i]) * std::log(1 - o_[i]) );
return J/m_;*/
T J{0.};
for (int i = 0; i < m_; ++i)
J += 1./2*std::pow(y_[i] - o_[i], 2);
return J/m_;
}
template<typename T>
T LogisticRegression2<T>::calculate_activation_function(T value) const
{
switch (activation_func_) {
case ActivationFunction::Sigmoid:
default: // Sigmoid
return ((T)1 / ((T)1 + std::exp(-value))); // y = 1/(1+exp(-value))
}
}
template<typename T>
T LogisticRegression2<T>::calculate_loss_function() const
{
switch (loss_func_) {
case LossFunction::MSE:
default: // MSE
T value = 0.;
for (int i = 0; i < m_; ++i) {
value += 1/2.*std::pow(y_[i] - o_[i], 2);
}
return value/m_;
}
}
template<typename T>
T LogisticRegression2<T>::calculate_loss_function_derivative() const
{
switch (loss_func_) {
case LossFunction::MSE:
default: // MSE
T value = 0.;
for (int i = 0; i < m_; ++i) {
value += o_[i] - y_[i];
}
return value/m_;
}
}
template<typename T>
T LogisticRegression2<T>::calculate_loss_function_derivative(unsigned int index) const
{
switch (loss_func_) {
case LossFunction::MSE:
default: // MSE
return (o_[index] - y_[index]);
}
}
template<typename T>
void LogisticRegression2<T>::calculate_gradient_descent()
{
switch (optim_) {
case Optimzation::BGD:
default: // BGD
T db = (T)0.;
std::vector<T> dw(feature_length_, (T)0.), z(m_, (T)0), dz(m_, (T)0);
for (int i = 0; i < m_; ++i) {
z[i] = calculate_z(x_[i]);
o_[i] = calculate_activation_function(z[i]);
dz[i] = calculate_loss_function_derivative(i);
for (int j = 0; j < feature_length_; ++j) {
dw[j] += x_[i][j] * dz[i]; // dw(i)+=x(i)(j)*dz(i)
}
db += dz[i]; // db+=dz(i)
}
for (int j = 0; j < feature_length_; ++j) {
dw[j] /= m_;
w_[j] -= alpha_ * dw[j];
}
b_ -= alpha_*(db/m_);
}
}
template class LogisticRegression2<float>;
template class LogisticRegression2<double>;
} // namespace ANN? ? ? test.cpp:
int test_logistic_regression2_train()
{
#ifdef _MSC_VER
const std::string image_path{ "E:/GitCode/NN_Test/data/images/digit/handwriting_0_and_1/" };
#else
const std::string image_path{ "data/images/digit/handwriting_0_and_1/" };
#endif
cv::Mat data, labels;
for (int i = 1; i < 11; ++i) {
const std::vector<std::string> label{ "0_", "1_" };
for (const auto& value : label) {
std::string name = std::to_string(i);
name = image_path + value + name + ".jpg";
cv::Mat image = cv::imread(name, 0);
if (image.empty()) {
fprintf(stderr, "read image fail: %s\n", name.c_str());
return -1;
}
data.push_back(image.reshape(0, 1));
}
}
data.convertTo(data, CV_32F);
std::unique_ptr<float[]> tmp(new float[20]);
for (int i = 0; i < 20; ++i) {
if (i % 2 == 0) tmp[i] = 0.f;
else tmp[i] = 1.f;
}
labels = cv::Mat(20, 1, CV_32FC1, tmp.get());
ANN::LogisticRegression2<float> lr;
const float learning_rate{ 0.00001f };
const int iterations{ 1000 };
int ret = lr.init((float*)data.data, (float*)labels.data, data.rows, data.cols);
if (ret != 0) {
fprintf(stderr, "logistic regression init fail: %d\n", ret);
return -1;
}
#ifdef _MSC_VER
const std::string model{ "E:/GitCode/NN_Test/data/logistic_regression2.model" };
#else
const std::string model{ "data/logistic_regression2.model" };
#endif
ret = lr.train(model);
if (ret != 0) {
fprintf(stderr, "logistic regression train fail: %d\n", ret);
return -1;
}
return 0;
}
int test_logistic_regression2_predict()
{
#ifdef _MSC_VER
const std::string image_path{ "E:/GitCode/NN_Test/data/images/digit/handwriting_0_and_1/" };
#else
const std::string image_path{ "data/images/digit/handwriting_0_and_1/" };
#endif
cv::Mat data, labels, result;
for (int i = 11; i < 21; ++i) {
const std::vector<std::string> label{ "0_", "1_" };
for (const auto& value : label) {
std::string name = std::to_string(i);
name = image_path + value + name + ".jpg";
cv::Mat image = cv::imread(name, 0);
if (image.empty()) {
fprintf(stderr, "read image fail: %s\n", name.c_str());
return -1;
}
data.push_back(image.reshape(0, 1));
}
}
data.convertTo(data, CV_32F);
std::unique_ptr<int[]> tmp(new int[20]);
for (int i = 0; i < 20; ++i) {
if (i % 2 == 0) tmp[i] = 0;
else tmp[i] = 1;
}
labels = cv::Mat(20, 1, CV_32SC1, tmp.get());
CHECK(data.rows == labels.rows);
#ifdef _MSC_VER
const std::string model{ "E:/GitCode/NN_Test/data/logistic_regression2.model" };
#else
const std::string model{ "data/logistic_regression2.model" };
#endif
ANN::LogisticRegression2<float> lr;
int ret = lr.load_model(model);
if (ret != 0) {
fprintf(stderr, "load logistic regression model fail: %d\n", ret);
return -1;
}
for (int i = 0; i < data.rows; ++i) {
float probability = lr.predict((float*)(data.row(i).data), data.cols);
fprintf(stdout, "probability: %.6f, ", probability);
if (probability > 0.5) fprintf(stdout, "predict result: 1, ");
else fprintf(stdout, "predict result: 0, ");
fprintf(stdout, "actual result: %d\n", ((int*)(labels.row(i).data))[0]);
}
return 0;
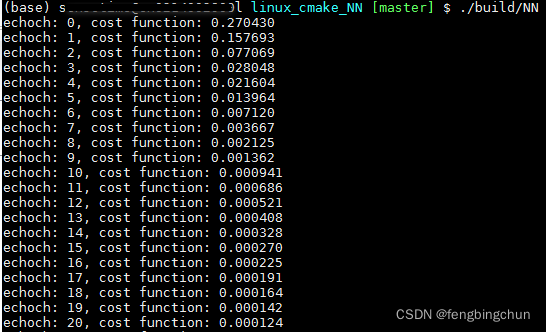
}? ? ? train执行结果如下:
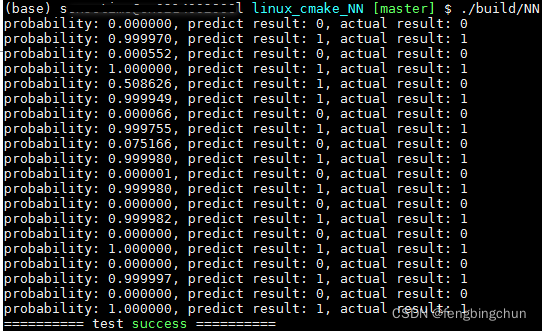
? ? ? predict执行结果如下:
? ? ? GitHub:?https://github.com/fengbingchun/NN_Test