WhitegiveCMA
题目链接,提取码:GAME
理论分析
下载后是一个文件
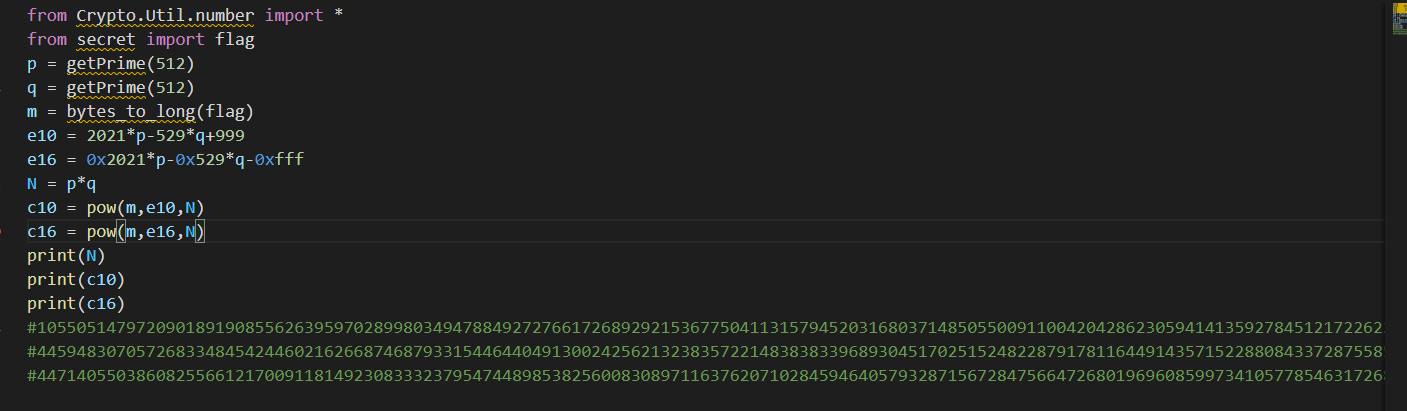
给出了两个e,考虑共模攻击。
为了方便后续阅读,做如下变形:
e 10 = a 1 ? p + b 1 ? q + d 1 e_{10} = a_1*p + b_1*q+d_1 e10?=a1??p+b1??q+d1?
e
16
=
a
2
?
p
+
b
2
?
q
+
d
2
e_{16}=a_2*p + b_2*q +d_2
e16?=a2??p+b2??q+d2?
a
1
=
2021
;
b
1
=
?
529
;
d
1
=
999
;
a
2
=
0
x
2021
;
b
2
=
?
0
x
529
;
d
2
=
0
x
f
f
f
;
a_1 = 2021; b_1 = -529; d_1 = 999;\\ a_2 = \rm 0x2021; b_2 = -\rm 0x529; d_2 = \rm 0xfff;
a1?=2021;b1?=?529;d1?=999;a2?=0x2021;b2?=?0x529;d2?=0xfff;
首先通过变换获取只与p,q相关的密文形式,记为 c p , c q c_p,c_q cp?,cq?
c p = c 10 b 2 × c 16 ? b 1 = m a 1 × b 2 × p ? a 2 × b 1 × p + d 1 × b 2 ? d 2 × d 1 c_p = c_{10}^{b_2}\times c_{16}^{-b_1} = m^{a_1\times b_2\times p-a_2\times b_1\times p+d_1\times b_2- d_2\times d_1} cp?=c10b2??×c16?b1??=ma1?×b2?×p?a2?×b1?×p+d1?×b2??d2?×d1?
c q = c 10 ? a 2 × c 16 a 1 = m a 1 × b 2 × q ? a 2 × b 1 × q + d 2 × a 1 ? d 1 × a 2 c_q = c_{10}^{-a_2}\times c_{16}^{a_1} = m^{a_1\times b_2\times q-a_2\times b_1\times q+d_2\times a_1- d_1\times a_2} cq?=c10?a2??×c16a1??=ma1?×b2?×q?a2?×b1?×q+d2?×a1??d1?×a2?
令
w = a 1 ? b 2 ? a 2 ? b 1 w = a_1*b_2 -a_2*b_1 w=a1??b2??a2??b1?
e p = b 2 ? d 1 ? b 1 ? d 2 + w e_p = b_2*d_1 -b_1*d_2 + w ep?=b2??d1??b1??d2?+w
e q = a 1 ? d 2 ? a 2 ? d 1 + w e_q = a_1*d_2 -a_2*d_1 +w eq?=a1??d2??a2??d1?+w
则
c p = m w ( p ? 1 ) + e p m o d N c_p = m^{w(p-1)}+e_p \quad mod \quad N cp?=mw(p?1)+ep?modN
c q = m w ( q ? 1 ) + e q m o d N c_q = m^{w(q-1)}+e_q \quad mod \quad N cq?=mw(q?1)+eq?modN
根据欧拉定理知道: m p ? 1 ≡ 1 m o d p m^{p-1} \equiv 1 \quad mod\quad p mp?1≡1modp, m q ? 1 ≡ 1 m o d q m^{q-1} \equiv 1 \quad mod \quad q mq?1≡1modq
所以 c p m o d p = m e p m o d p , c q m o d q = m e q m o d q c_p\quad mod\quad p = m^{e_p}\quad mod \quad p,\quad c_q\quad mod\quad q = m^{e_q}\quad mod\quad q cp?modp=mep?modp,cq?modq=meq?modq
令
k p = c p e q m o d N k_p = c_p^{e_q} mod\quad N kp?=cpeq??modN
k q = c q e p m o d N k_q = c_q^{e_p} mod\quad N kq?=cqep??modN
如果知道 k = m e p × e q m o d N k = m^{e_p\times e_q}mod \quad N k=mep?×eq?modN
则由
k
p
=
x
1
?
p
+
m
e
q
?
e
p
k
q
=
x
2
?
q
+
m
e
q
?
e
p
K
=
x
3
?
N
+
m
e
q
?
e
p
x
1
,
x
2
,
x
3
∈
Z
k
p
?
k
=
p
?
(
x
1
?
x
3
?
q
)
k
q
?
k
=
q
?
(
x
1
?
x
3
?
p
)
k_p = x_1*p + m^{e_q*e_p}\\ k_q = x_2*q + m^{e_q*e_p}\\ K = x_3*N + m^{e_q*e_p}\\ x_1,x_2,x_3 \in \Z\\ k_p - k = p*(x_1-x_3*q)\\ k_q - k = q*(x_1-x_3*p)
kp?=x1??p+meq??ep?kq?=x2??q+meq??ep?K=x3??N+meq??ep?x1?,x2?,x3?∈Zkp??k=p?(x1??x3??q)kq??k=q?(x1??x3??p)
由以上信息可知
k
p
?
k
k_p-k
kp??k是p的倍数,
k
q
?
k
k_q-k
kq??k是q的倍数,则有:
(
k
p
?
k
)
?
(
k
q
?
k
)
≡
0
m
o
d
N
p
=
g
c
d
(
k
p
?
k
,
N
)
q
=
g
c
d
(
k
q
?
k
,
N
)
(k_p - k )*(k_q - k ) \equiv 0 \quad mod \quad N\\ p = gcd(k_p-k,N)\\ q = gcd(k_q-k,N)
(kp??k)?(kq??k)≡0modNp=gcd(kp??k,N)q=gcd(kq??k,N)
为了能求出K,一个方程还不行。可以构造
c
0
=
(
c
p
?
c
q
)
e
p
?
e
q
=
m
e
p
?
e
q
?
(
w
(
p
?
1
)
+
e
p
+
w
(
q
?
1
)
+
e
q
=
m
e
P
?
e
q
?
(
w
(
p
+
q
?
2
)
+
e
p
+
e
q
)
=
k
w
?
(
p
+
q
?
2
)
+
e
p
+
e
q
m
o
d
N
c_0 = (c_p* c_q)^{e_p*e_q}\quad \\ =m^{e_p*e_q*(w(p-1)+e_p+w(q-1)+e_q}\\ =m^{e_P*e_q*(w(p+q-2)+e_p+e_q)}\\ = k^{w*(p+q-2)+e_p+e_q}\quad mod \quad N
c0?=(cp??cq?)ep??eq?=mep??eq??(w(p?1)+ep?+w(q?1)+eq?=meP??eq??(w(p+q?2)+ep?+eq?)=kw?(p+q?2)+ep?+eq?modN
又因为
k
(
p
?
1
)
?
(
q
?
1
)
≡
1
m
o
d
N
k^{(p-1)*(q-1)} \equiv 1 \quad mod \quad N
k(p?1)?(q?1)≡1modN
所以
c
0
=
k
w
?
N
?
w
+
e
q
+
e
p
m
o
d
N
e
0
=
w
?
N
?
w
+
e
q
+
e
p
c_0= k^{w*N - w + e_q+e_p} \quad mod \quad N\\ e_0= w*N - w + e_q+e_p
c0?=kw?N?w+eq?+ep?modNe0?=w?N?w+eq?+ep?
此时有
(
k
p
?
k
)
?
(
k
q
?
k
)
≡
0
m
o
d
N
c
0
=
k
w
?
N
?
w
+
e
q
+
e
p
m
o
d
N
(k_p - k )*(k_q - k ) \equiv 0 \quad mod \quad N\\ c_0= k^{w*N - w + e_q+e_p} \quad mod \quad N\\
(kp??k)?(kq??k)≡0modNc0?=kw?N?w+eq?+ep?modN
其中只有k是未知数,所以可以考虑共模攻击。
把两个方程看为两个多项式,第一个 k 2 = ( k p + k q ) ? k ? k p ? k q m o d N k^2 =(k_p+k_q)*k - k_p*k_q \quad mod\quad N k2=(kp?+kq?)?k?kp??kq?modN
一般化:
(
a
1
?
k
+
b
1
)
?
(
a
2
?
k
+
b
2
)
=
a
1
?
a
2
?
k
2
+
(
a
1
?
b
2
+
a
2
?
b
1
)
?
k
+
(
b
1
?
b
2
)
(a_1*k+b_1)*(a_2*k+b_2) = a_1*a_2*k^2 + (a_1*b_2+a_2*b_1)*k+(b_1*b_2)
(a1??k+b1?)?(a2??k+b2?)=a1??a2??k2+(a1??b2?+a2??b1?)?k+(b1??b2?)
将
k
2
=
(
k
p
+
k
q
)
?
k
?
k
p
?
k
q
m
o
d
N
k^2 =(k_p+k_q)*k - k_p*k_q \quad mod\quad N
k2=(kp?+kq?)?k?kp??kq?modN两边同时乘以
a
1
a
2
a_1a_2
a1?a2?展开
( a 1 ? b 2 + a 2 ? b 1 + a 1 ? a 2 ? ( k p + k q ) ? k + ( b 1 ? b 2 ? a 1 ? a 2 ? k p ? k q ) (a_1*b_2+a_2*b_1+a_1*a_2*(k_p+k_q)*k+(b_1*b_2-a_1*a_2*k_p*k_q) (a1??b2?+a2??b1?+a1??a2??(kp?+kq?)?k+(b1??b2??a1??a2??kp??kq?)
只要确定 a 1 , b 1 , a 2 , b 2 a_1,b_1,a_2,b_2 a1?,b1?,a2?,b2?即可求出解,
def mul(a1,b1,a2,b2):
return (a1*b2+a2*b1+a1*a2*(Kp+Kq))%N,(b1*b2-a1*a2*Kp*Kq)%N
根据上述等式用多项式的二分乘法把pow(K,e0,N)化成关于K的一次多项式
a0 = 1
b0 = 0
a = 0
b = 1
while(e0):
if(e0%2):
a,b = mul(a,b,a0,b0)
a0,b0 = mul(a0,b0,a0,b0)
e0 = e0//2
化为一次多项式后,有 a ? k ≡ b m o d N a*k\equiv b \quad mod \quad N a?k≡bmodN,即可求出k
K = ((c0-b)*inverse(a,N))%N
根据上面方程可以求出p,q。最后求出结果
完整代码
import binascii
import gmpy2
# 数据
N = 105505147972090189190855626395970289980349478849272766172689292153677504113157945203168037148505500911004204286230594141359278451217226220464199578711317870524009399925159330085268891611702732693725184219479126235131294548787119706541901289970313500513673347826843758751748580989418278226520156936626924327059
c10 = 44594830705726833484542446021626687468793315446440491300242562132383572214838383396893045170251524822879178116449143571522880843372875585376945929248227672182668860765415910480567064826316000549996363948338866696321566948086096629421501295545617054417677393365598002537621340410326525247666639842346491047367
c16 = 44714055038608255661217009118149230833323795474489853825600830897116376207102845946405793287156728475664726801969608599734105778546317268118984070287308254520723161252793270372766239693849125114583526383289679577470203270954263611671265610573237844472924495914342697052049517874123620614228215081764500905625
a1 = 2021
b1 = -529
d1 = 999
a2 = 0x2021
b2 = -0x529
d2 = -0xfff
# 获取cp和cq。
cp = gmpy2.powmod(c16,-b1,N)*gmpy2.powmod(c10,b2,N)%N
cq = gmpy2.powmod(c10,-a2,N)*gmpy2.powmod(c16,a1,N)%N
w = a1*b2-b1*a2
ep = b2*d1-b1*d2+w
eq = a1*d2-a2*d1+w
Kp = gmpy2.powmod(cp,eq,N)
Kq = gmpy2.powmod(cq,ep,N)
c0 = gmpy2.powmod(cp*cq,ep*eq,N)
e0 = w*N+ep+eq-w
def mul(a1,b1,a2,b2):
return (a1*b2+a2*b1+a1*a2*(Kp+Kq))%N,(b1*b2-a1*a2*Kp*Kq)%N
# 把pow(K,e0,N)化成关于K的一次多项式。
a0 = 1
b0 = 0
a = 0
b = 1
while(e0):
if(e0%2):
a,b = mul(a,b,a0,b0)
a0,b0 = mul(a0,b0,a0,b0)
e0 = e0//2
# 得到关于K的一元一次方程,求解
K = ((c0-b)*gmpy2.invert(a,N))%N
# 再分解N
p = gmpy2.gcd(Kp-K,N)
q = gmpy2.gcd(Kq-K,N)
# 解密
e10 = a1*p+b1*q+d1
e16 = a2*p+b2*q+d2
d = gmpy2.invert(e16,(p-1)*(q-1))
m = gmpy2.powmod(c16,d,N)
flag = binascii.unhexlify(hex(m)[2:])
print(flag)