文章目录
1. 基本流程
(1)定义
一般的,一棵决策树包含一个根节点、若干内部节点和叶节点。
- 叶节点:对应决策结果。
- 根节点和中间节点:根据属性测试的结果将所属样本划分到其子节点中。
(2)决策树基本算法
决策树的生成是一个递归过程。
- 在每次递归中,首先判断是否达到递归返回条件,获得叶节点。
- 选择最优化分节点。
- 根据节点的属性测试结果将包含的样本划分到子节点。
- 以子节点为子树根节点,剔除当前最优划分属性,调用决策树生成函数。

(3)三种递归返回情况
- 当前D中所有样本都属于同一类别C时:
将Node标记为类型为C的叶节点。 - 当前属性集A为空:
多数投票,将Node标记为当前样本集合D中数量最多类别的叶节点。 - 当前样本集D为空
将Node标记为其父节点样本中数量最多的类的叶节点。
2. 划分选择
我们希望随着划分的不断进行,决策树的分支节点的纯度越来越高,分支节点所包含的样本尽可能属于同一类别。
| 属性 | 缺点 | 方法 | 内容 |
|---|---|---|---|
| 信息增益 | 对可取值数目较多的属性有所偏好 | ID3 | 选择信息增益最大的属性 |
| 信息增益率 | 对可取值数目较多的属性有所偏好 | C4.5 | 从候选划分属性找出信息增益高于平均水平的属性,再从中选取增益率最高 |
| 基尼指数 | CART | 选择划分后基尼指数最小的属性 |
2.1 信息增益(information gain)
(1)信息熵
信息熵(information entropy)是度量样本纯度最常用的一种指标。
E
n
t
(
D
)
=
?
∑
k
=
1
∣
γ
∣
p
k
log
?
2
p
k
Ent(D)=-\sum_{k=1}^{|\gamma|} p_k \log_2 p_k
Ent(D)=?k=1∑∣γ∣?pk?log2?pk?
度量: E n t ( D ) Ent(D) Ent(D)值越小,惊异值越小,纯度越高。
- 假设当 p k = 0 p_k=0 pk?=0时, p k log ? 2 p k = 0 p_k \log_2 p_k =0 pk?log2?pk?=0。
- 当 p k = 1 p_k=1 pk?=1时, E n t ( D ) Ent(D) Ent(D)值最小为0。当 p k = 1 ∣ γ ∣ p_k=\frac{1}{|\gamma|} pk?=∣γ∣1?时,即样本按类别1:1分布时, E n t ( D ) Ent(D) Ent(D)值最大为1.
理解: 信息熵用于度量某一样本集D的纯度。只要给定样本集就可以计算其对应的信息熵。
(2)信息增益(information entropy)
假设离散属性
α
\alpha
α有
V
V
V个可能的取值为
{
a
1
,
a
2
,
?
?
,
a
V
}
\{a_1,a_2,\cdots,a_V\}
{a1?,a2?,?,aV?},用
α
\alpha
α来进行划分,会产生
V
V
V个分支节点。其中第v各分支节点包含了D中所有在属性
α
\alpha
α上取值为
a
v
a_v
av?的样本,记为
D
v
D^v
Dv。
可以计算出用属性
α
\alpha
α对样本D进行划分所得到的信息增益:
G
a
i
n
(
D
,
α
)
=
E
n
t
(
D
)
?
∑
i
=
1
V
∣
D
i
∣
∣
D
∣
E
n
t
(
D
i
)
Gain(D,\alpha)=Ent(D)-\sum_{i=1}^V \frac{|D^i|}{|D|}Ent(D^i)
Gain(D,α)=Ent(D)?i=1∑V?∣D∣∣Di∣?Ent(Di)
其中, ∣ D i ∣ ∣ D ∣ \frac{|D^i|}{|D|} ∣D∣∣Di∣?为该分支节点 a i a_i ai?的权重,样本数越多分支节点的影响越大。
- 信息增益 = 划分前的信息上 - 划分后各分支节点信息熵的加权和。
- 一般而言,信息增益越大,则意味着使用 α \alpha α来进行划分所获得的纯度提升越大。
(3)实例分析
以色泽属性为例,计算按色泽划分后的信息增益:
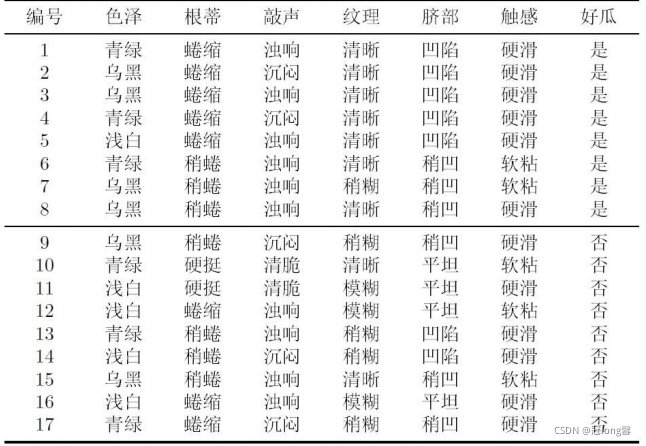
- 计算划分前样本集D的信息熵
E n t ( D ) = 8 17 l o g 2 8 17 + 9 17 l o g 2 9 17 = 0.998 Ent(D)=\frac{8}{17}log_2\frac{8}{17}+\frac{9}{17}log_2\frac{9}{17}=0.998 Ent(D)=178?log2?178?+179?log2?179?=0.998 - 以属性色泽为划分,计算信息增益。
①对应的三个子集分别为 D 1 青 绿 = { 1 , 4 , 6 , 10 , 13 , 17 } , D 2 乌 黑 = { 2 , 3 , 7 , 8 , 9 , 15 } , D 3 浅 白 = { 5 , 11 , 12 , 14 , 16 } D^{1青绿}=\{1,4,6,10,13,17\},D^{2乌黑}=\{2,3,7,8,9,15\},D^{3浅白}=\{5,11,12,14,16\} D1青绿={1,4,6,10,13,17},D2乌黑={2,3,7,8,9,15},D3浅白={5,11,12,14,16}
②计算各子节点的信息熵:
E n t ( D 1 ) = 1 E n t ( D 2 ) = ? ( 2 3 l o g 2 2 3 + 1 3 l o g 2 1 3 ) = 0.918 E n t ( D 3 ) = ? ( 1 5 l o g 2 1 5 + 4 5 l o g 2 4 5 ) = 0.722 Ent(D^1)=1 \\ Ent(D^2)=-(\frac{2}{3}log_2\frac{2}{3}+\frac{1}{3}log_2\frac{1}{3})=0.918 \\ Ent(D^3)=-(\frac{1}{5}log_2\frac{1}{5}+\frac{4}{5}log_2\frac{4}{5})=0.722 Ent(D1)=1Ent(D2)=?(32?log2?32?+31?log2?31?)=0.918Ent(D3)=?(51?log2?51?+54?log2?54?)=0.722
③计算信息增益:
G a i n ( D , α ) = 0.998 ? ( 6 17 × 1 + 6 17 × 0.918 + 5 17 × 0.722 ) = 0.109 Gain(D,\alpha)=0.998-(\frac{6}{17}\times 1+\frac{6}{17} \times 0.918+\frac{5}{17} \times 0.722)=0.109 Gain(D,α)=0.998?(176?×1+176?×0.918+175?×0.722)=0.109
(4)缺点
信息增益对可取值数目较多的属性有所偏好。
2.2 信息增益率
(1)定义
G
a
i
n
_
r
a
t
i
o
n
(
D
,
a
)
=
G
a
i
n
(
D
,
a
)
I
V
(
a
)
I
V
(
a
)
=
?
∑
v
=
1
V
∣
D
v
∣
∣
D
∣
l
o
g
2
∣
D
v
∣
∣
D
∣
Gain\_ration(D,a) = \frac{Gain(D,a)}{IV(a)} \\ IV(a)=-\sum_{v=1}^{V}\frac{|D^v|}{|D|} log_2 \frac{|D^v|}{|D|}
Gain_ration(D,a)=IV(a)Gain(D,a)?IV(a)=?v=1∑V?∣D∣∣Dv∣?log2?∣D∣∣Dv∣?
其中, I V ( a ) IV(a) IV(a)为属性a的固定值。属性a的可能取值数目越多(V越大),则IV(a)的值通常越大。
(2)缺点
信息增益率对可取值数目较少的属性有所偏好。
(3)C4.5启发式算法
先从候选划分属性找出信息增益高于平均水平的属性,再从中选取增益率最高的。
理解: 信息增益率在信息增益的基础上除以了属性的固定值,以期削弱对可取值数目较多属性的偏好。但是固定值的出现,也导致信息增益率对可取值数目较少的属性有所偏好。
2.3 基尼指数
(1)基尼值
数据集D的纯度可用“基尼值”来度量。基尼值反应了从D中随机抽取两个样本,其类别标记不一致的概率。
G
i
n
i
(
D
)
=
1
?
∑
k
=
1
∣
y
∣
p
k
2
Gini(D)=1-\sum_{k=1}^{|y|}p_k^2
Gini(D)=1?k=1∑∣y∣?pk2?
- Gini(D)越小,数据集D的纯度越高
(2)基尼指数
G
i
n
i
_
i
n
d
e
x
(
D
,
a
)
=
∑
v
=
1
∣
V
∣
∣
D
v
∣
∣
D
∣
G
i
n
i
(
D
v
)
a
?
=
arg
?
min
?
a
∈
A
G
i
n
i
_
i
n
d
e
x
(
D
,
a
)
Gini\_index(D,a)=\sum_{v=1}^{|V|}\frac{|D^v|}{|D|}Gini(D^v) \\ a_* = \arg \min_{a \in A} Gini\_index(D,a)
Gini_index(D,a)=v=1∑∣V∣?∣D∣∣Dv∣?Gini(Dv)a??=arga∈Amin?Gini_index(D,a)
- 选择划分后基尼指数最小的属性作为最优划分属性。
3. 剪枝
决策树训练过程中,为了尽可能正确分类训练样本,节点划分过程不断重复,有时会造成决策树分支过多而导致过拟合。因此可以用过主动去掉一些分支来降低过拟合的风险。
决策树剪枝的基本策略有“预剪枝”和“后剪枝”。
- 预剪枝:每个节点在划分前先进行估计。若当前节点的划分不能带来泛化性能的提升,则停止划分并将节点当作叶节点。
- 后剪枝:先从训练集生成一棵完整的决策树,然后自底向上地对非叶节点进行考察。若将节点对应的子树替换成叶节点能对决策树带来泛化性能的提升,则将子树替换为叶节点。
| 优点 | 缺点 | |
|---|---|---|
| 预剪枝 | 1.显著减少训练时间和测试时间开销。2. 降低过拟合风险 | 欠拟合风险 |
| 后剪枝 | 1.欠拟合风险小。2. 泛化能力往往优于预剪枝 | 训练时间开销大 |
3.1 划分验证集
可以采用留出法,预留一部分数据用作验证集,以进行性能评估。
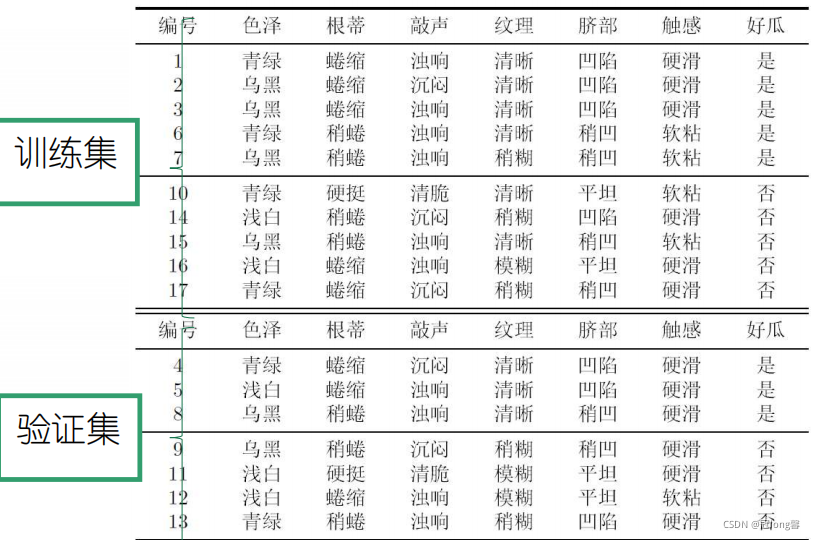
- 训练集{1,2,3,6,7,10,14,15,16,17}
- 验证集{4,5,8,9,11,12,13}
3.2 预剪枝
(1)思路
当划分节点前先进行评估。若当前节点划分不能带来泛化性能的提升,则停止划分并将当前节点当作叶节点。
(2)步骤
- Step1: 计算将节点当作叶节点时在验证集上的精度pre1。
- Step2: 计算节点划分后在验证集上的精度pre2。
- Step3: 若 p r e 2 > p r e 1 pre2 > pre1 pre2>pre1,即划分能带来泛化性能的提高,则按照当前属性划分。否则,采取多数投票法则将节点看作叶节点。
(3)样例分析
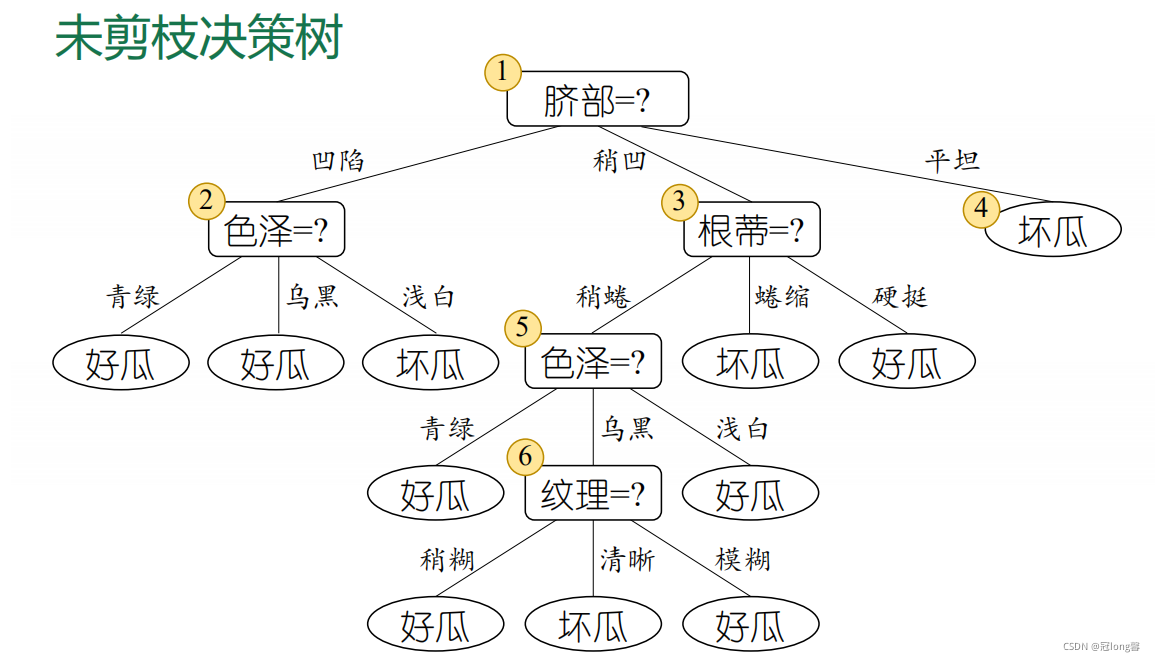
- 若不对脐部划分,并将其标记为叶节点:
① 根据当前节点的样本集,其中标记为好瓜的个数大于坏瓜的数目 5 > 4 5>4 5>4,将叶节点类别标记为好瓜。
② 验证集中{4,5,8}分类正确,验证集精度为 3 7 ? 100 = 42.9 % \frac{3}{7} *100 =42.9 \% 73??100=42.9% - 若对脐部进行划分,划分结果如下:
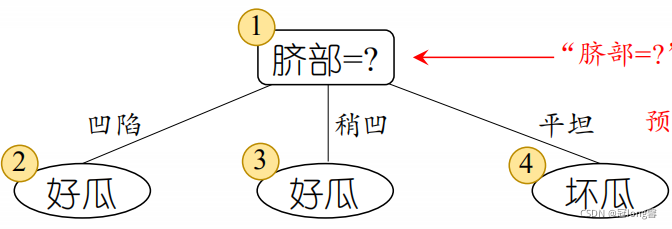
此时,验证集中{4,5,8,11,12}划分正确,验证集精度为: 5 7 × 100 = 71.4 % \frac{5}{7} \times 100 = 71.4 \% 75?×100=71.4% - 划分后验证集的精度提升,则按照脐部进行划分。
对脐部为凹陷的样本进行预剪枝判断:
首先选择出“色泽“为其最佳划分属性。
-
若不对色泽划分,并将其标记为叶节点:
① 根据当前节点的样本集,其中标记为好瓜的个数大于坏瓜的数目 3 > 1 3>1 3>1,将叶节点类别标记为好瓜。
此时,验证集中{4,5,8,11,12}划分正确,验证集精度为: 5 7 × 100 = 71.4 % \frac{5}{7} \times 100 = 71.4 \% 75?×100=71.4% -
若对色泽进行划分,划分结果如下:
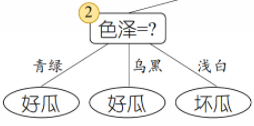
此时,验证集中{4,8,11,12}划分正确,验证集精度为: 4 7 × 100 = 57.1 % \frac{4}{7} \times 100 =57.1 \% 74?×100=57.1% -
划分后验证集的精度降低,故将凹陷节点当作标签为好瓜的叶节点。
(4)优缺点
优点
- 降低过拟合风险
- 显著减少训练时间和测试时间开销
缺点
- 欠拟合风险
有些分支当前划分虽然不能提升泛化性能,但在其基础上进行得后续划分却有可能导致性能显著提高。
3.3 后剪枝
(1)思想
先从训练集生成一棵完整的决策树,然后自底向上地对非叶节点进行考察。若将节点对应的子树替换成叶节点能对决策树带来泛化性能的提升,则将子树替换为叶节点。
(2)步骤
- Step1: 从训练集生成一颗完整的决策树。
- Step2: 自底向上对非叶节点考察,计算将节点对应子树替换成叶节点后在验证集上的精确度。
- Step3: 若替换后精度上升,则将子树替换为叶节点。
(3)样例分析

决策树在验证集上的精度为{4、11、12}:
3
/
7
=
42.9
%
3 / 7 = 42.9 \%
3/7=42.9%
- 考虑节点⑥。节点包含样本集为”稍凹、微蜷、乌黑“D={7、15}.将其替换为叶节点,节点标签为好瓜。此时,决策树在验证集上的精度为{4、8、11、12}:
4 7 = 57.1 % \frac{4}{7}=57.1\% 74?=57.1% - 替换为叶节点后,验证集上精度提升。于是决定剪枝。剪枝后的决策树如图:

(4)优缺点
优点
- 欠拟合风险小。
- 泛化能力往往优于预剪枝。
缺点
- 训练时间开销大。
3.4 预剪枝和后剪枝的选择
预剪枝能显著减少训练时间并避免过拟合,但是又欠拟合的风险。后剪枝训练时间开销较大,但泛化能力往往更强。因此得到如下结论:
- ① 数据量较小时 ==> 后剪枝
- ② 数据量较大时 ==> 预剪枝
4. 连续与缺失值
4.1 连续值处理
因为连续属性的可能取值不再有限,因此不能直接根据连续属性的可能取值对节点进行划分。最常用的策略是二分法对连续属性进行处理。
(1)二分法
给定样本集D和连续属性a,假定a在D上出现了n个不同的取值,将这些值从小到大进行排序,记为
a
1
,
a
2
,
?
?
,
a
n
{a^1,a^2,\cdots,a^n}
a1,a2,?,an。基于划分点t可将D分为子集
D
t
?
,
D
t
+
D_t^-,D_t^+
Dt??,Dt+?。
- 对于连续属性,我们考虑包含 n ? 1 n-1 n?1个元素的候选划分点集合:
T a = { a i + a i + 1 2 ∣ 1 ≤ i ≤ n ? 1 } T_a=\{\frac{a_i+a_{i+1}}{2}|1 \leq i \leq n-1 \} Ta?={2ai?+ai+1??∣1≤i≤n?1}
- 然后选取最优的划分点进行样本集合划分:
G a i n ( D , a ) = max ? t ∈ T a G a i n ( D , a , t ) G a i n _ i n d e x ( D , a ) = max ? t ∈ T a G a i n _ i n d e x ( D , a , t ) G i n i _ i n d e x ( D , a ) = min ? t ∈ T a ∑ v = 1 ∣ V ∣ ∣ D v ∣ ∣ D ∣ G i n i ( D v , t ) Gain(D,a) = \max_{t \in T_a}Gain(D,a,t) \\ Gain\_index(D,a) = \max_{t \in T_a} Gain\_index(D,a,t) \\ Gini\_index(D,a)=\min_{t \in T_a} \sum_{v=1}^{|V|}\frac{|D^v|}{|D|}Gini(D^v,t) Gain(D,a)=t∈Ta?max?Gain(D,a,t)Gain_index(D,a)=t∈Ta?max?Gain_index(D,a,t)Gini_index(D,a)=t∈Ta?min?v=1∑∣V∣?∣D∣∣Dv∣?Gini(Dv,t)
注意
- 若当前节点划分属性为连续属性,该属性还可作为后代节点的划分属性。
4.2 缺失值处理
若简单地放弃不完整样本,仅使用无缺失值的样本进行学习,是对数据信息极大的浪费。对于缺失值,我们需要解决两个问题:
- 如何在属性缺失的情况下进行划分属性选择。
- 给定划分属性,若样本在属性上的值缺失,如何对样本进行划分。
理解:如何解决划分属性选择和样本分类两个问题。
(1)定义
给定训练集
D
D
D和属性a。
- 令 D ^ \hat{D} D^表示D中在属性a上没有缺失值的样本子集。
- 令 D ^ v \hat{D}^v D^v表示 D ^ \hat{D} D^中属性a上取值为 a v a^v av的样本子集。
- 令 D ^ k \hat{D}_k D^k?表示 D ^ \hat{D} D^中属于第k类( k = 1 , 2 , ? ? , ∣ γ ∣ k=1,2,\cdots,|\gamma| k=1,2,?,∣γ∣)的样本子集。
- 假定为每个样本x赋予一个权重 w x w_x wx?,初始化为1.
- 无缺失值样本所占比例
ρ
\rho
ρ:
ρ = ∑ x ∈ D ^ w x ∑ x ∈ D w x \rho = \frac{\sum_{x \in \hat{D}}w_x}{\sum_{x \in D}w_x} ρ=∑x∈D?wx?∑x∈D^?wx?? - 无缺失样本中第k类所占的比例
p
k
^
\hat{p_k}
pk?^?:
p k ^ = ∑ x ∈ D ^ k w x ∑ x ∈ D ^ w x \hat{p_k} = \frac{\sum_{x \in \hat{D}_k}w_x}{\sum_{x \in \hat{D}}w_x} pk?^?=∑x∈D^?wx?∑x∈D^k??wx?? - 无缺失样本中在属性a上取值为
a
v
a^v
av的样本所占比例
r
v
^
\hat{r_v}
rv?^?:
r v ^ = ∑ x ∈ D ^ v w x ∑ x ∈ D ^ w x \hat{r_v} = \frac{\sum_{x \in \hat{D}^v}w_x}{\sum_{x \in \hat{D}}w_x} rv?^?=∑x∈D^?wx?∑x∈D^v?wx??
(2)最优划分属性
基于上述定义,可以将信息增益的计算式推广为:
G
a
i
n
(
D
,
a
)
=
ρ
×
G
a
i
n
(
D
^
,
a
)
=
ρ
×
(
E
n
t
(
D
^
)
?
∑
v
=
1
V
r
^
v
E
n
t
(
D
v
^
)
)
Gain(D,a) = \rho \times Gain(\hat{D},a) \\ =\rho \times (Ent(\hat{D})-\sum_{v=1}^V \hat{r}^vEnt(\hat{D^v}))
Gain(D,a)=ρ×Gain(D^,a)=ρ×(Ent(D^)?v=1∑V?r^vEnt(Dv^))
E n t ( D ^ ) = ? ∑ k = 1 ∣ γ ∣ p k ^ log ? p k ^ Ent(\hat{D})=-\sum_{k=1}^{|\gamma|}\hat{p_k} \log \hat{p_k} Ent(D^)=?k=1∑∣γ∣?pk?^?logpk?^?
(3)样本分类
- 若样本划分属性a上的取值已知,则将x划入其取值对应的子节点。
- 若取值未知,则将x同时划入所有子节点,各自节点中样本的权值调整为 r v ^ \hat{r^v} rv^