文章目录
第三课——神经网络Ⅰ
神经网络引入
逻辑回归的二阶段表示
逻辑回归
输入与输出之间的映射关系如下
P
(
y
=
1
∣
x
;
w
,
b
)
=
1
1
+
e
?
(
w
T
x
+
b
)
P(y=1|x;w,b)=\frac{1}{1+e^{-(w^Tx+b)}}
P(y=1∣x;w,b)=1+e?(wTx+b)1?
其中,𝑥为输入特征,𝑦为输出标记
y
=
{
0
,
1
}
y=\{0,1\}
y={0,1}(即二分类任务),𝒘,𝑏为学习参数。
𝒘是权重,b是偏值bias
逻辑回归的二阶段表示
1?? 求和summing function
R
P
→
R
R^P\rightarrow R
RP→R
z = w T x + b = w 1 x 1 + . . . + w p x p + b z=w^Tx+b=w_1x_1+...+w_px_p+b z=wTx+b=w1?x1?+...+wp?xp?+b
2?? 挤压sigmoid function
R
→
{
0
,
1
}
R\rightarrow \{0,1\}
R→{0,1}
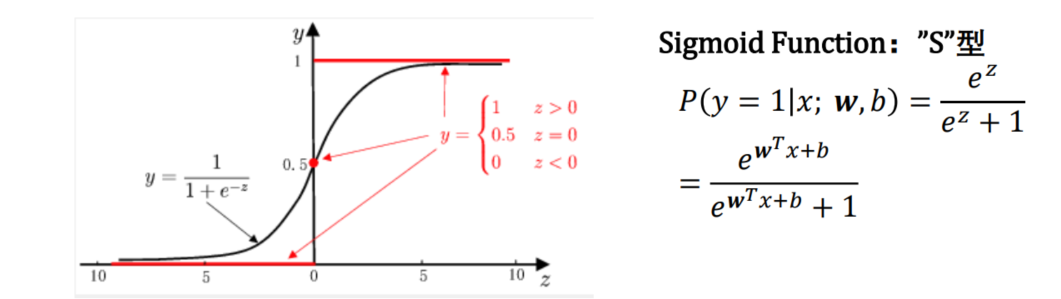
y ^ = P ( y = 1 ∣ x ; w , b ) = 1 1 + e ? z = e z e z + 1 \hat y=P(y=1|x;w,b)=\frac{1}{1+e^{-z}}=\frac{e^{z}}{e^z+1} y^?=P(y=1∣x;w,b)=1+e?z1?=ez+1ez?
挤压函数就是之前逻辑回归学到的sigmoid function:

神经元
在生物神经网络中,每个神经元与其它神经元相连,当它“兴奋”时,向其它神经元发送化学物质。
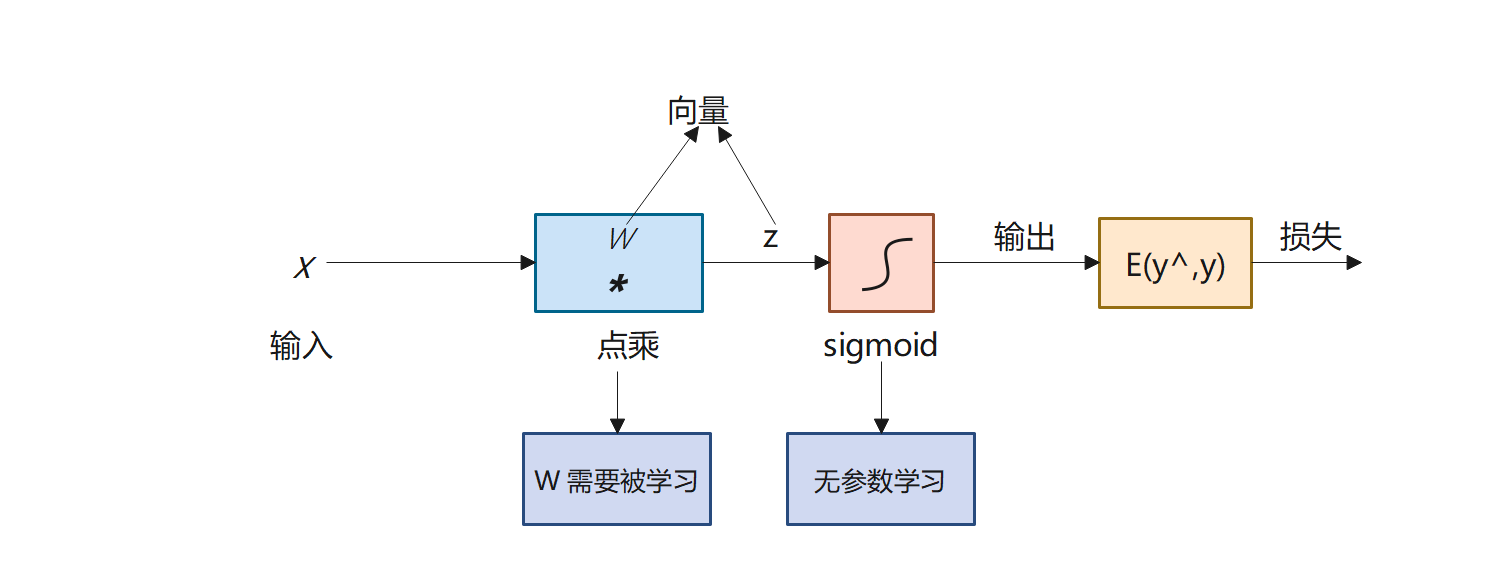
在机器学习中,将生物模型抽象为下图所示的简单神经网络模型。神经元接收来自其它神经元传递过来的输入信号,输入信号通过带权重的连接进行传递,然后通过“激活函数”产生神经元输出

神经元:一个神经元是由线性变换和非线性变换共同构成的
因此,逻辑回归是包含一个神经元的神经网络
神经网络
神经网络包含多个神经元,输入𝒙与多个神经元相连。W需要从向量扩展为矩阵。
𝑊𝑖𝑗表示的向量x的第𝑗个元素与向量𝑍的第𝑖个元素之间的连接权重
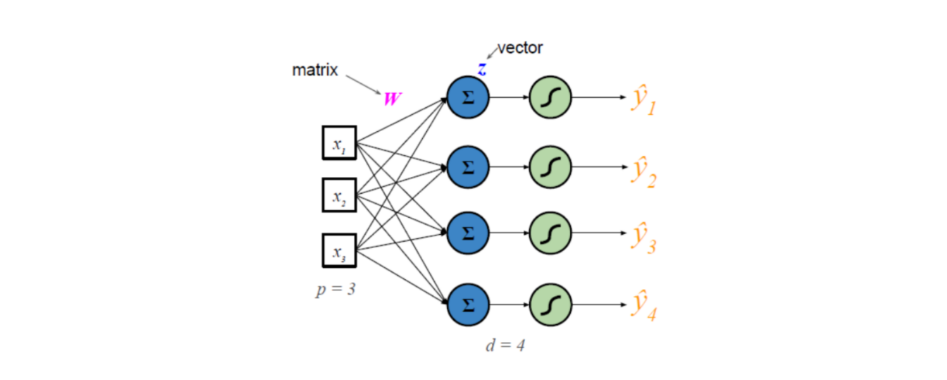
对于上图的神经网络,W如下:
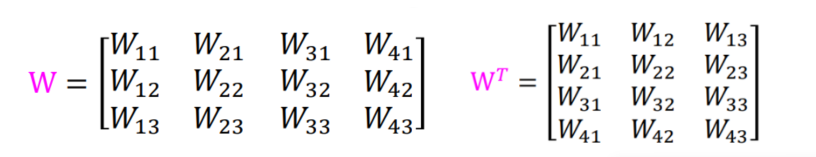
具有一个隐藏层的神经网络
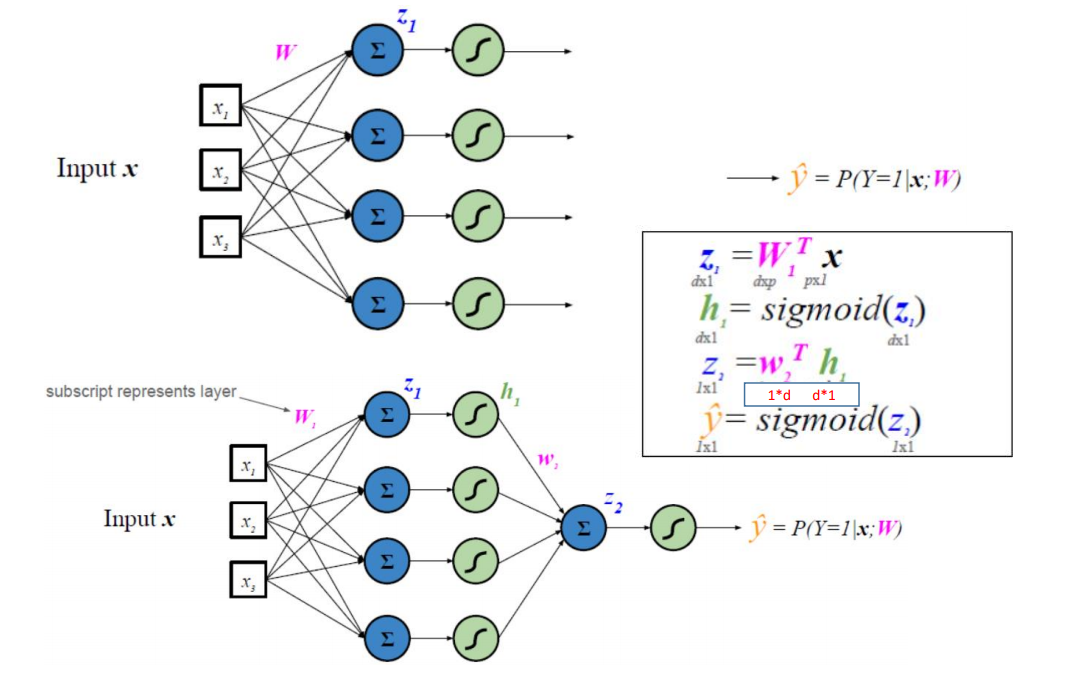
构造特征的特征

h1是隐藏层的输出
具有两个隐藏层的神经网络
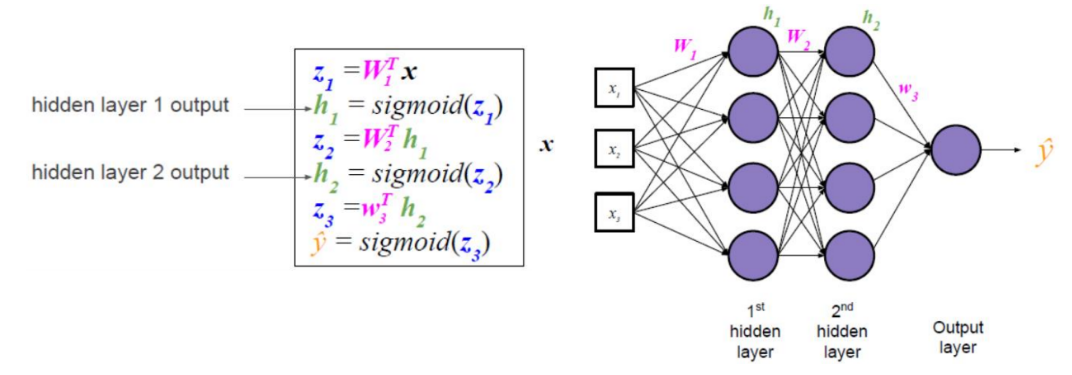
1?? 多元线性回归直接建立了输入和输出的关系
2?? 逻辑回归利用一个summing function和sigmoid function建立了输入和输出的关系
3?? 神经网络利用了多个summing function和sigmoid function建立了输入和输出的关系
神经网络本质上就是一个复合函数
这里都是全连接
非线性激活函数
引入非线性激活函数的目的是得到非线性决策面
不论网络多深,线性激活函数只能输出线性决策面(输出是输入的线性函数)。
非线性激活函数可以逼近任意复杂函数。


当 y ^ = 1 2 \hat y=\frac{1}{2} y^?=21?是无法进行判断的,此时使之成立的边界称为决策面
常用的非线性激活函数
| 名字 | 图形 | 方程 | 导数 |
|---|---|---|---|
| Binary step | 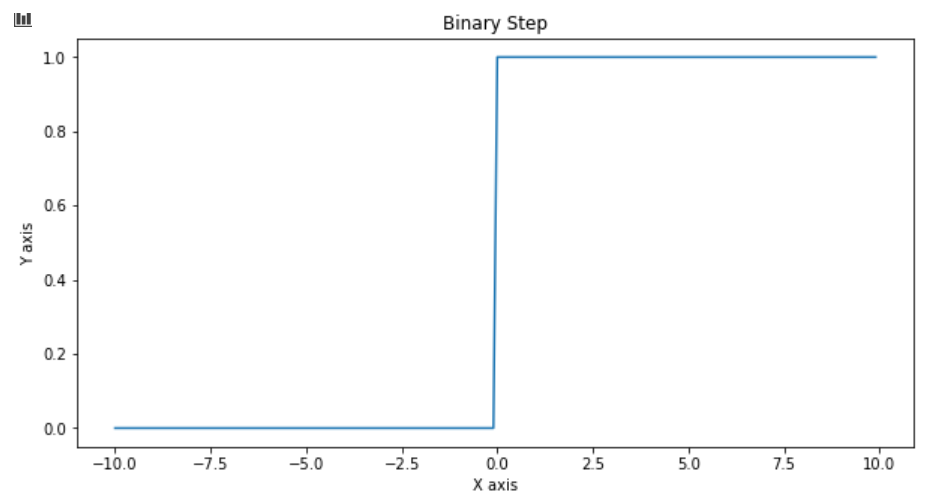 | 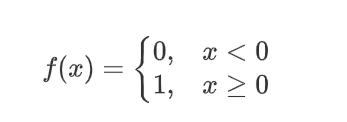 | 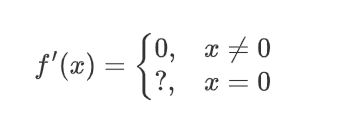 |
| Logistic(a.k.a Soft step) | 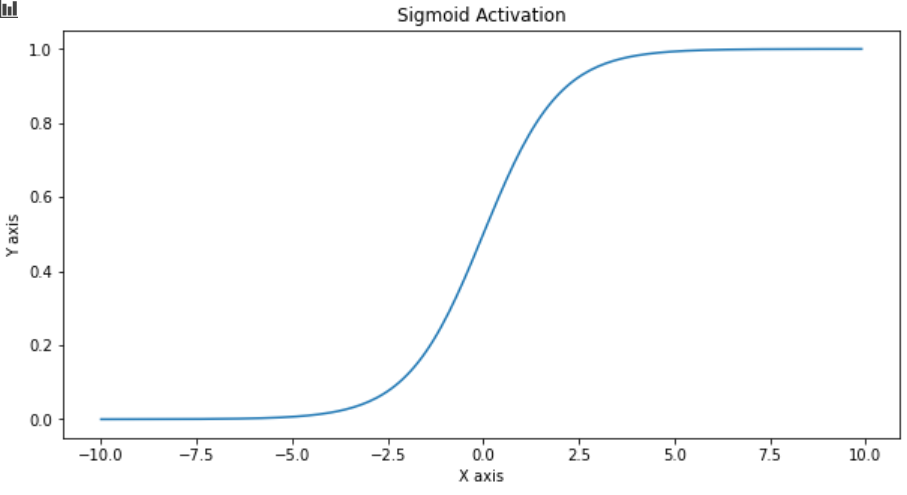 | 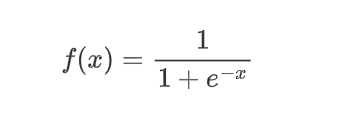 | 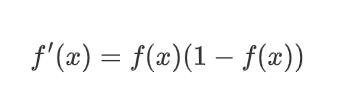 |
| TanH | 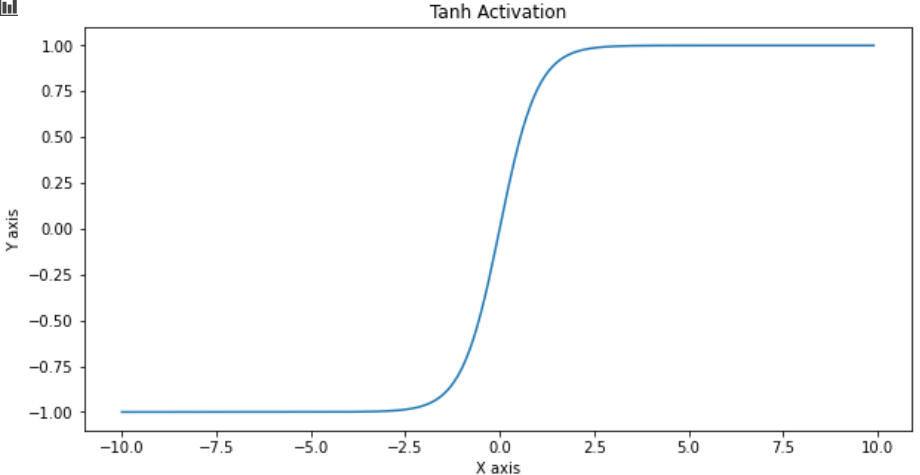 | 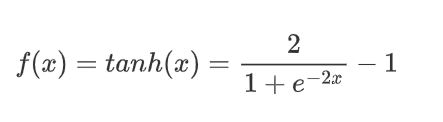 | 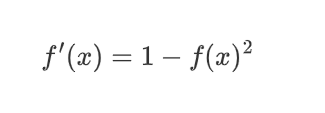 |
| ReLU | 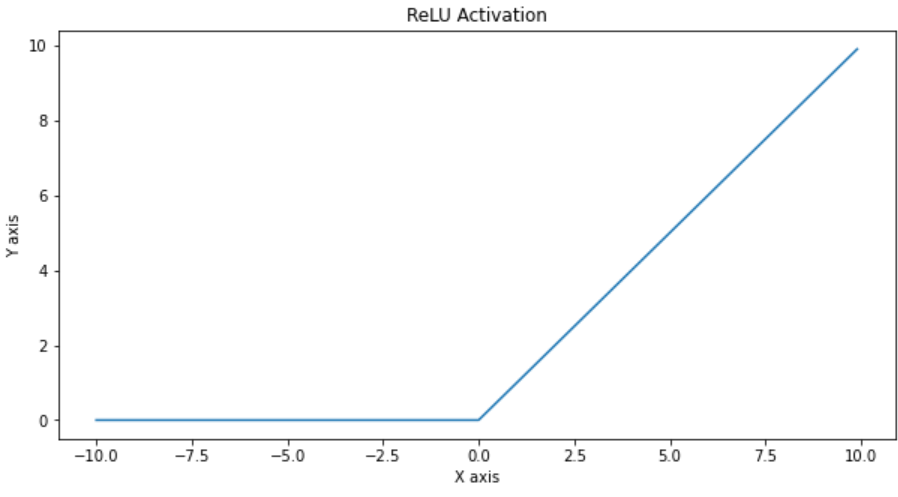 | 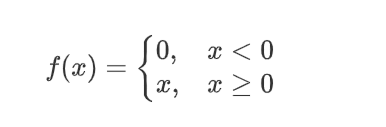 | 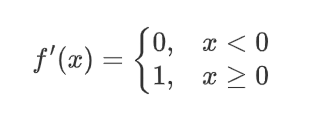 |
Hidden layer(隐层)的个数大于1的神经网络,称为深度神经网络
训练神经网络
损失函数
二分类损失
逻辑回归中,使用对数似然度量损失(每个样本属于其真实标记的概率越大越好)
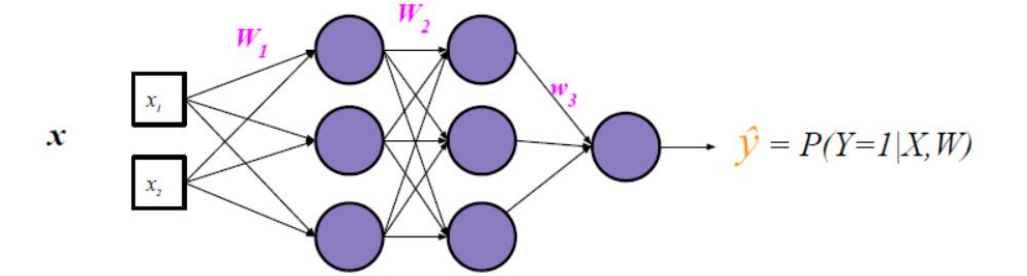
交叉熵代价函数cross entropy loss
E
=
l
o
s
s
=
?
log
?
P
(
Y
=
y
^
∣
X
=
x
)
=
?
y
log
?
(
y
^
)
?
(
1
?
y
)
log
?
(
1
?
y
^
)
E=loss=-\log P(Y=\hat y|X=x)=-y\log(\hat y)-(1-y)\log(1-\hat y)
E=loss=?logP(Y=y^?∣X=x)=?ylog(y^?)?(1?y)log(1?y^?)
y y y是真实输出, y ^ \hat y y^?是预测输出
y ^ = f θ ( x ) = e w x + b e w x + b + 1 \hat y =f_\theta(x)=\frac{e^{wx+b}}{e^{wx+b}+1} y^?=fθ?(x)=ewx+b+1ewx+b?
损失函数一定是一个标量
多分类损失
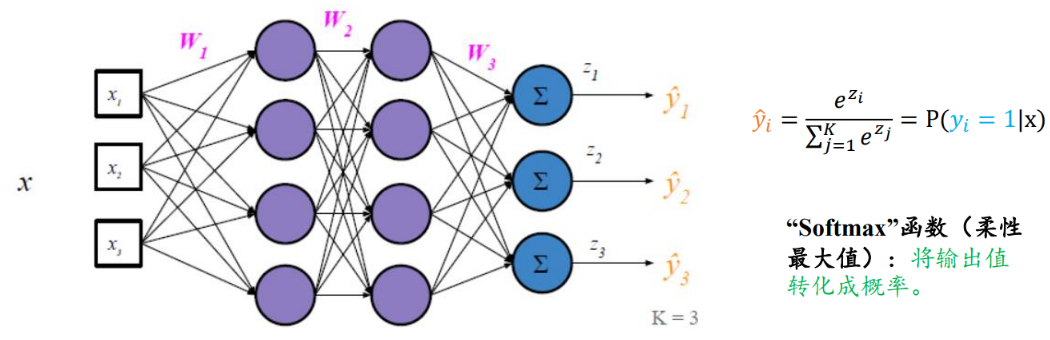
Softmax函数:将各个输出节点的输出值范围映射到[0,1],并且约束各个输出节点的输出值的和为1的函数
交叉熵代价函数cross entropy loss
E
=
l
o
s
s
=
?
∑
j
=
1
,
.
.
.
,
K
y
j
log
?
y
^
j
E=loss=-\sum_{j=1,...,K}y_j\log\hat y_j
E=loss=?j=1,...,K∑?yj?logy^?j?
其中 y j y_j yj?是One-Hot向量:真实标签的位置为1,其他位置为0
One-Hot编码,又称为一位有效编码,主要是采用N位状态寄存器来对N个状态进行编码,每个状态都由他独立的寄存器位,并且在任意时候只有一位有效。
例如,对于
y
T
=
(
0
?
1
?
0
)
,
y
^
T
=
(
?
0.1
?
0.7
?
0.2
)
y^T=(0 \ 1\ 0),\hat y^T=(\ 0.1\ 0.7\ 0.2)
yT=(0?1?0),y^?T=(?0.1?0.7?0.2),其损失函数为
E
=
?
(
0
×
log
?
0.1
+
1
×
log
?
0.7
+
0
×
log
?
0.2
)
=
?
log
?
0.7
E=-(0\times \log0.1+1\times\log0.7+0\times\log0.2)=-\log 0.7
E=?(0×log0.1+1×log0.7+0×log0.2)=?log0.7
E
=
l
o
s
s
=
1
2
∣
∣
y
?
y
^
2
∣
∣
=
1
2
∑
j
=
1
K
(
y
j
?
y
^
j
)
2
E=loss=\frac{1}{2}||y-\hat y^2||=\frac{1}{2}\sum^K_{j=1}(y_j-\hat y_j)^2
E=loss=21?∣∣y?y^?2∣∣=21?j=1∑K?(yj??y^?j?)2
回归损失
与分类网络的不同之处:输出层不再包含“Sigmoid”函数
使用二次代价函数
E
=
l
o
s
s
=
1
2
∣
∣
y
?
y
^
2
∣
∣
=
1
2
∑
j
=
1
K
(
y
j
?
y
^
j
)
2
E=loss=\frac{1}{2}||y-\hat y^2||=\frac{1}{2}\sum^K_{j=1}(y_j-\hat y_j)^2
E=loss=21?∣∣y?y^?2∣∣=21?j=1∑K?(yj??y^?j?)2
反向传播
目标:寻找使损失达到最小的神经网络权重
如何学习神经网络权重𝑊𝐿?使用梯度下降 W L ( t + 1 ) = W L ( t ) ? η ? E ? W L ( t ) W_L(t+1)=W_L(t)-\eta \frac{\partial E}{\partial W_L(t)} WL?(t+1)=WL?(t)?η?WL?(t)?E?
其中 η \eta η为学习率
如何得到𝑊1,…,𝑊𝐿?1层的权重?使用反向传播Backpropagation
重复应用微积分的链式法则
局部最小化目标函数
要求网络所有的“块”(blocks)都是可微的
数学符号说明
Hadamard (哈达玛)乘积/schur 乘积:
假设𝑠和𝑡是两个同样维度的向量,使用𝑠°𝑡(或𝑠⊙𝑡)来表示按元素的乘积: (𝑠⊙𝑡)𝑗= 𝑠𝑗𝑡𝑗
[
1
2
]
⊙
[
3
4
]
=
[
1
?
3
2
?
4
]
=
[
3
8
]
\begin{bmatrix} 1\\2 \end{bmatrix} \odot \begin{bmatrix} 3\\4 \end{bmatrix} =\begin{bmatrix} 1*3\\2*4 \end{bmatrix}= \begin{bmatrix} 3\\8 \end{bmatrix}
[12?]⊙[34?]=[1?32?4?]=[38?]
回归示例
就是复合函数求偏导
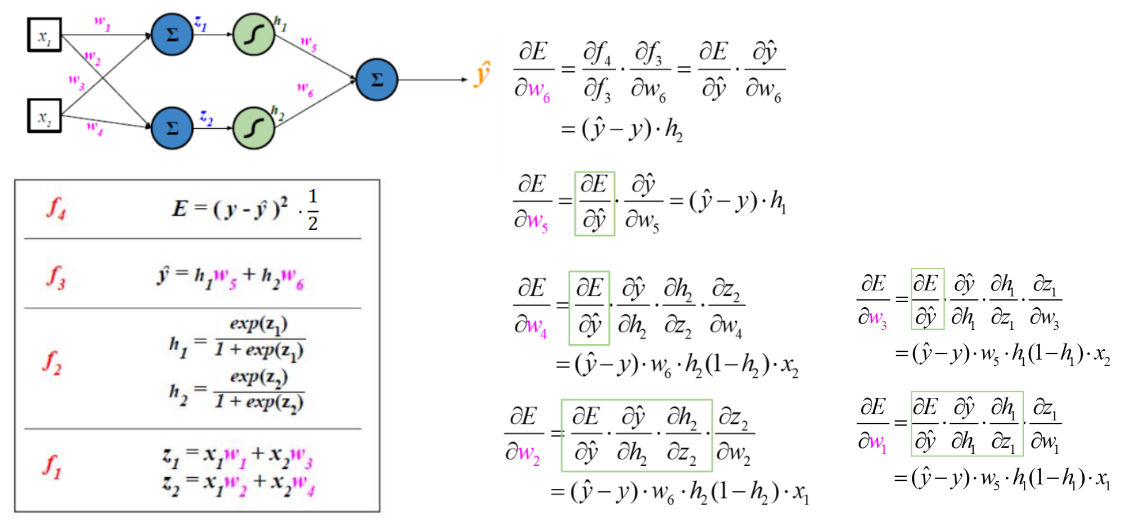
可见已经比较复杂了
二分类示例
包含一个隐层的二分类神经网络:
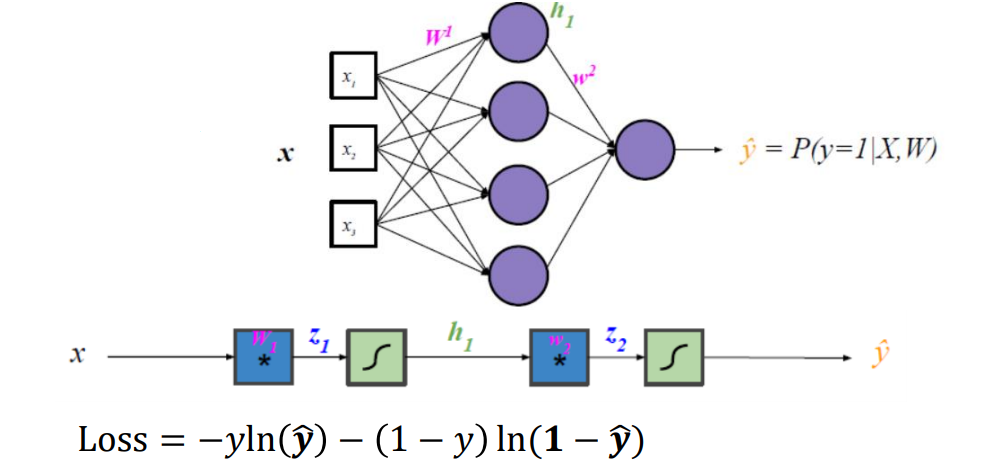
对w2的偏导求解还比较简单

对W1的偏导就复杂很多


w i j 1 w_{ij}^1 wij1?表示输入𝒙 的第𝑗个元素到第1个隐层的 第 𝑖个神经元的权重
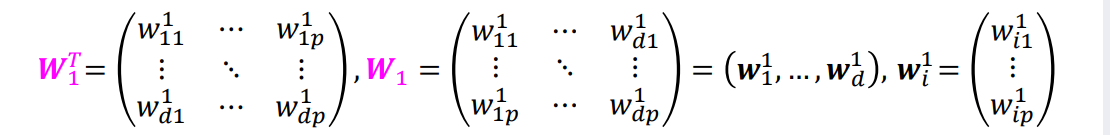
首先推导关于𝑾𝟏的第一列 w 1 1 w_1^1 w11?求导结果,然后推导到第j列,最后得到关于这个矩阵的偏导
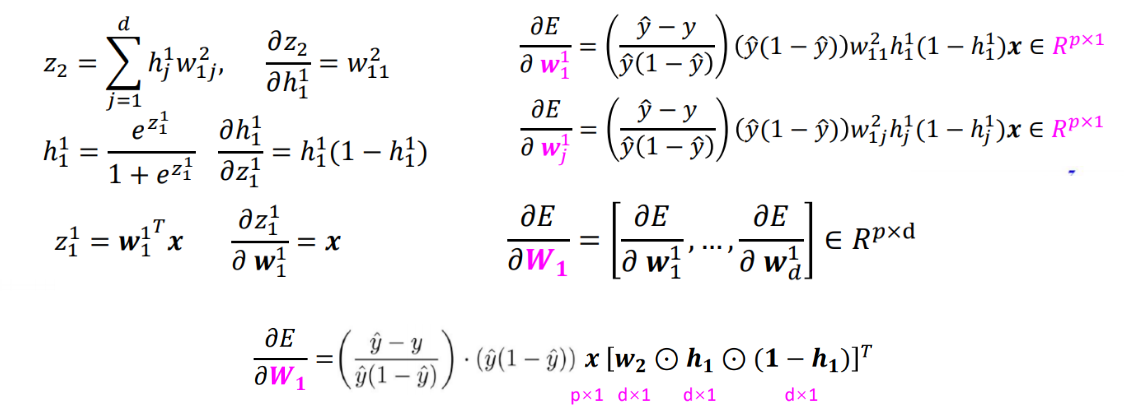
深度神经网络学习
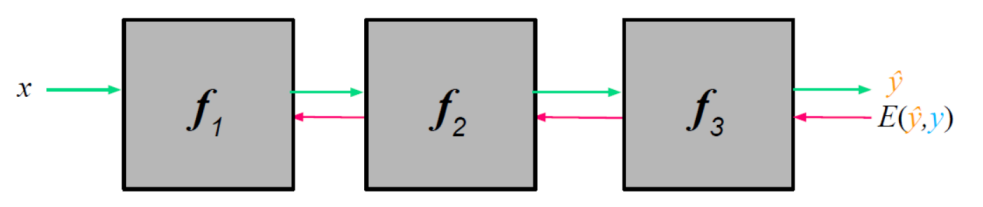
前向传播加反向传播
| 传播方向 | 前向传播 | 反向传播 |
|---|---|---|
| 步骤 | 1、给定一个初始的权重W | 1、计算误差损失 E ( y , y ^ ) E(y,\hat y) E(y,y^?) |
| 2、输入x | 2、通过链式法则(复合函数求导)计算梯度 | |
| 3、通过复合函数 y ^ = f 3 ( f 2 ( f 1 ( x ) ) ) \hat y=f_3(f_2(f_1(x))) y^?=f3?(f2?(f1?(x)))计算预测值 | ||
| 更新内容 | 已知边,更新圆圈内容 | 已知圆圈内容,更新边(权重) |
重复迭代前向和反向步骤,直至算法收敛。
参考资料
[1]庞善民.西安交通大学机器学习导论2022春PPT
[2]周志华.机器学习.北京:清华大学出版社,2016