摘要
? ? ? ?上一篇文章实验是基于凯斯西厨大学轴承数据集,使用同一负载情况下的6种轴承数据进行故障诊断,并没有进行不同负载下轴承故障诊断。之前没做这块迁移学习实验,主要是对于迁移学习理解不到位,也没有不知道从什么方向去做。趁写论文这段时间,看了很多的文献资料,对于迁移学习其实有了一点点理解。迁移学习其实涉及两个概念,分别是源域、目标域。源域可以理解为用于模型训练的数据集,而目标域其实是我们需要去预测的数据集。但是往往源域数据集和目标域数据集之间是存在不同程度的数据分布差异。而目前的深度学习能够实现这么高的准确度,其实也是默认数据具有相同的数据分布。因此,根据自己的理解,结合之前所搜集到的资源,利用MK-MMD方法实现不同负载下的轴承故障诊断研究。本人也只是做了一种情况下的迁移,主要是希望起到抛砖引玉的效果,有什么不对的地方多多谅解。
数据集
1.数据来源
? ? ? ? 实验所用的数据集还是凯斯西厨大学的轴承数据集(注:本人实验室没有实验的平台,无法获取真实的轴承数据集)。实验平台如图1。

?图1 凯斯西储大学轴承数据集
2.时频变换生成时频图像
? ? ? ? 在上一篇文章的基础上,直接对负载为0、负载为3情况下的十种故障振动信号,进行数据增强操作,再使用连续小波变换将一维振动图像转换为二维时频图像。变化得到的效果图如下图2所示。
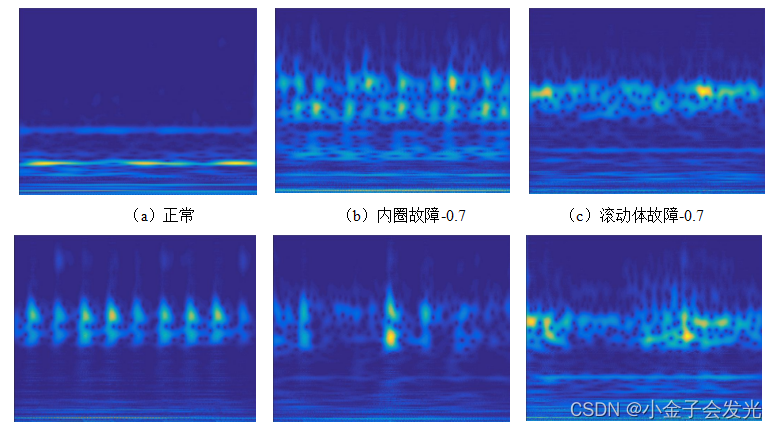
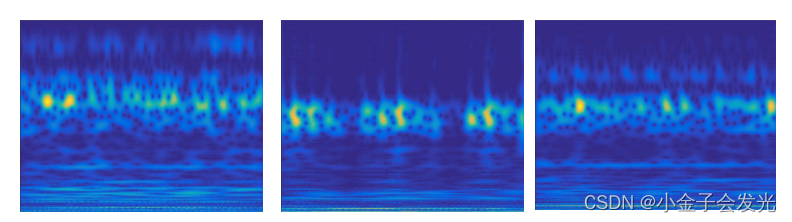
?图2 负载为0下的轴承时频变换图像

图3?负载为3下的轴承时频变换图像
? ? ? ? 其实通过观看时频图像,我们可以看到负载1下和负载3下的十种轴承故障时频图像相差不大,文章后面会利用MK-MMD验证,确实确定了两个数据的分布差异并不大。
?迁移学习
1.概念
? ? ? ?迁移学习的概念可以参考王晋东的迁移学习导论pdf,上面对于迁移学习的概念讲的很清楚。不再进行具体的介绍。迁移学习的基本概念如下图4所示。其中涉及源域和目标域两个概念。

图4 迁移学习基本概念
2.迁移学习的领域自适应问题
? ? ? ? 迁移学习领域自适应问题主要是如何解决源域数据和目标域数据间分布的差异,并利用方法进行有效地减少这种差异,使得源域数据和目标域数据分布尽可能地一致。具体表示如下图5所示。

?图5?领域自适应问题
? ? ? ?谈到迁移学习的领域自适问题,必定会涉及边缘分布、条件分布。因为源域数据和目标域数据差异主要表现边缘分布、条件分布上。因此,如何缩小源域数据和目标域数据的问题实质就是如何缩小边缘分布、条件分布。
2.1边缘分布
? ? ? ? 边缘分布概念如下图6所示。不要看着边缘分布很高大上,其实质也就是利用不同的数学手段,将源域数据整体分布中心、目标域整体数据分布中心对齐重合,拉近两数据间的分布。边缘分布强调的是不同领域数据的整体分布对齐。
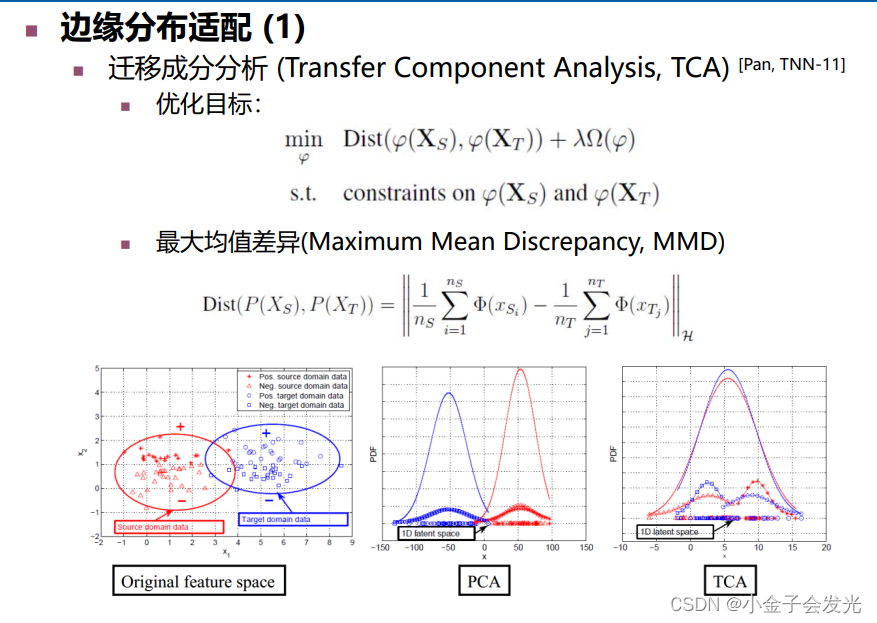
?图6?边缘分布
2.2条件分布
? ? ? ?条件分布如下图7所示。条件分布实质就是利用数学手段,将不同工况下的同一种类别的数据进行拉近,缩小数据的分布差异。而条件分布强调的是不同领域下相同类别数据的对齐。

?图7?条件分布
? ? ? ? 迁移学习的条件分布和边缘分布只要了解其概念就行,不需要对公式死扣,网上有很多的现成的代码给你调用。
2.3联合分布自适应
? ? ? ?联合分布自适应如下图8所示。联合实质就是结合条件分布、边缘分布分布相加,虽然表达式时上用的加号,但是实际不是简单的相加。这个也不用理解很深入,只需要了解联合分布的概念和原理就行。联合分布算法有TCA、JDA、BDA等,这些算法代码都可以在下方链接下载:
TCA、JDA、BDA等领域自适应算法都可以找到代码
https://github.com/jindongwang/transferlearning

?2.4相似度量方法
? ? ? ? 相似性度量是一种测量两个数据分布相似性的方法,通常使用距离测量两个样本数据分布的差异性,两者距离越大差异性越大,距离越小差异越小。在迁移学习的域自适应中,比较常用的相似度量方法有最大均值差异MMD和多核的 MMD 度量(MK-MMD)两种相似性度量方法。 本次实验就是利用的MK-MMD算法进行迁移训练。
(1)最大均值差异
? ? ? ?MMD 定义为再生核希尔伯特空间(Reproducing Kernel Hilbert Space,RKHS)中数据分布的核嵌入距离的平方。近年来,MMD 被广泛应用到域自适应中,以最小化源域和目标域之间的 MMD 距离为优化目标来进行特征的跨域自适应。具体计算公式如下所示:

MMD的具体代码如下所示。
import numpy as np
from sklearn import metrics
def mmd_linear(X, Y):
"""MMD using linear kernel (i.e., k(x,y) = <x,y>)
Note that this is not the original linear MMD, only the reformulated and faster version.
The original version is:
def mmd_linear(X, Y):
XX = np.dot(X, X.T)
YY = np.dot(Y, Y.T)
XY = np.dot(X, Y.T)
return XX.mean() + YY.mean() - 2 * XY.mean()
Arguments:
X {[n_sample1, dim]} -- [X matrix]
Y {[n_sample2, dim]} -- [Y matrix]
Returns:
[scalar] -- [MMD value]
"""
delta = X.mean(0) - Y.mean(0)
return delta.dot(delta.T)
def mmd_rbf(X, Y, gamma=1.0):
"""MMD using rbf (gaussian) kernel (i.e., k(x,y) = exp(-gamma * ||x-y||^2 / 2))
Arguments:
X {[n_sample1, dim]} -- [X matrix]
Y {[n_sample2, dim]} -- [Y matrix]
Keyword Arguments:
gamma {float} -- [kernel parameter] (default: {1.0})
Returns:
[scalar] -- [MMD value]
"""
XX = metrics.pairwise.rbf_kernel(X, X, gamma)
YY = metrics.pairwise.rbf_kernel(Y, Y, gamma)
XY = metrics.pairwise.rbf_kernel(X, Y, gamma)
return XX.mean() + YY.mean() - 2 * XY.mean()
def mmd_poly(X, Y, degree=2, gamma=1, coef0=0):
"""MMD using polynomial kernel (i.e., k(x,y) = (gamma <X, Y> + coef0)^degree)
Arguments:
X {[n_sample1, dim]} -- [X matrix]
Y {[n_sample2, dim]} -- [Y matrix]
Keyword Arguments:
degree {int} -- [degree] (default: {2})
gamma {int} -- [gamma] (default: {1})
coef0 {int} -- [constant item] (default: {0})
Returns:
[scalar] -- [MMD value]
"""
XX = metrics.pairwise.polynomial_kernel(X, X, degree, gamma, coef0)
YY = metrics.pairwise.polynomial_kernel(Y, Y, degree, gamma, coef0)
XY = metrics.pairwise.polynomial_kernel(X, Y, degree, gamma, coef0)
return XX.mean() + YY.mean() - 2 * XY.mean()
if __name__ == '__main__':
a = np.arange(1, 10).reshape(3, 3)
b = [[7, 6, 5], [4, 3, 2], [1, 1, 8], [0, 2, 5]]
b = np.array(b)
print(a)
print(b)
print(mmd_linear(a, b)) # 6.0
print(mmd_rbf(a, b)) # 0.5822
print(mmd_poly(a, b)) # 2436.5?(2)MK-MMD

? ? ? ?MK-MMD的具体代码如下所示。
def guassian_kernel(source, target, kernel_mul=2.0, kernel_num=5, fix_sigma=None):
'''
多核或单核高斯核矩阵函数,根据输入样本集x和y,计算返回对应的高斯核矩阵
Params:
source: (b1,n)的X分布样本数组
target:(b2,n)的Y分布样本数组
kernel_mul: 多核MMD,以bandwidth为中心,两边扩展的基数,比如bandwidth/kernel_mul, bandwidth, bandwidth*kernel_mul
kernel_num: 取不同高斯核的数量
fix_sigma: 是否固定,如果固定,则为单核MMD
Return:
sum(kernel_val): 多个核矩阵之和
'''
# 堆叠两组样本,上面是X分布样本,下面是Y分布样本,得到(b1+b2,n)组总样本
n_samples = int(source.shape[0]) + int(target.shape[0])
total = np.concatenate((source, target), axis=0)
# 对总样本变换格式为(1,b1+b2,n),然后将后两维度数据复制到新拓展的维度上(b1+b2,b1+b2,n),相当于按行复制
total0 = np.expand_dims(total, axis=0)
total0 = np.broadcast_to(total0, [int(total.shape[0]), int(total.shape[0]), int(total.shape[1])])
# 对总样本变换格式为(b1+b2,1,n),然后将后两维度数据复制到新拓展的维度上(b1+b2,b1+b2,n),相当于按复制
total1 = np.expand_dims(total, axis=1)
total1 = np.broadcast_to(total1, [int(total.shape[0]), int(total.shape[0]), int(total.shape[1])])
# total1 - total2 得到的矩阵中坐标(i,j, :)代表total中第i行数据和第j行数据之间的差
# sum函数,对第三维进行求和,即平方后再求和,获得高斯核指数部分的分子,是L2范数的平方
L2_distance_square = np.cumsum(np.square(total0 - total1), axis=2)
# 调整高斯核函数的sigma值
if fix_sigma:
bandwidth = fix_sigma
else:
bandwidth = np.sum(L2_distance_square) / (n_samples ** 2 - n_samples)
# 多核MMD
# 以fix_sigma为中值,以kernel_mul为倍数取kernel_num个bandwidth值(比如fix_sigma为1时,得到[0.25,0.5,1,2,4]
bandwidth /= kernel_mul ** (kernel_num // 2)
bandwidth_list = [bandwidth * (kernel_mul ** i) for i in range(kernel_num)]
# print(bandwidth_list)
# 高斯核函数的数学表达式
kernel_val = [np.exp(-L2_distance_square / bandwidth_temp) for bandwidth_temp in bandwidth_list]
# 得到最终的核矩阵
return sum(kernel_val) # 多核合并
def MK_MMD(source, target, kernel_mul=2.0, kernel_num=5, fix_sigma=None):
'''
计算源域数据和目标域数据的MMD距离
Params:
source: (b1,n)的X分布样本数组
target:(b2,n)的Y分布样本数组
kernel_mul: 多核MMD,以bandwidth为中心,两边扩展的基数,比如bandwidth/kernel_mul, bandwidth, bandwidth*kernel_mul
kernel_num: 取不同高斯核的数量
fix_sigma: 是否固定,如果固定,则为单核MMD
Return:
loss: MK-MMD loss
'''
batch_size = int(source.shape[0]) # 一般默认为源域和目标域的batchsize相同
kernels = guassian_kernel(source, target,kernel_mul=kernel_mul, kernel_num=kernel_num, fix_sigma=fix_sigma)
# 将核矩阵分成4部分
loss = 0
for i in range(batch_size):
s1, s2 = i, (i + 1) % batch_size
t1, t2 = s1 + batch_size, s2 + batch_size
loss += kernels[s1, s2] + kernels[t1, t2]
loss -= kernels[s1, t2] + kernels[s2, t1]
# 这里计算出的n_loss是每个维度上的MK-MMD距离,一般还会做均值化处理
n_loss = loss / float(batch_size)
return np.mean(n_loss)
? ? ? ? 上面两种度量方式了解基本的原理就行,不需要理解公式中的各项关系,还是那一句话,现成的代码都是有的,直接拿来用就行。
3.迁移学习分类
? ? ? ?迁移学习的分类大概了解一下就行,清楚每一个类型大概的原理,一般论文中用的比较多的是基于特征的迁移学习方法。其实这个方法也一直是轴承故障诊断研究中的热点问题。因此本章主要介绍基于特征的迁移学习方法。常用的迁移学习方式如下图8所示。
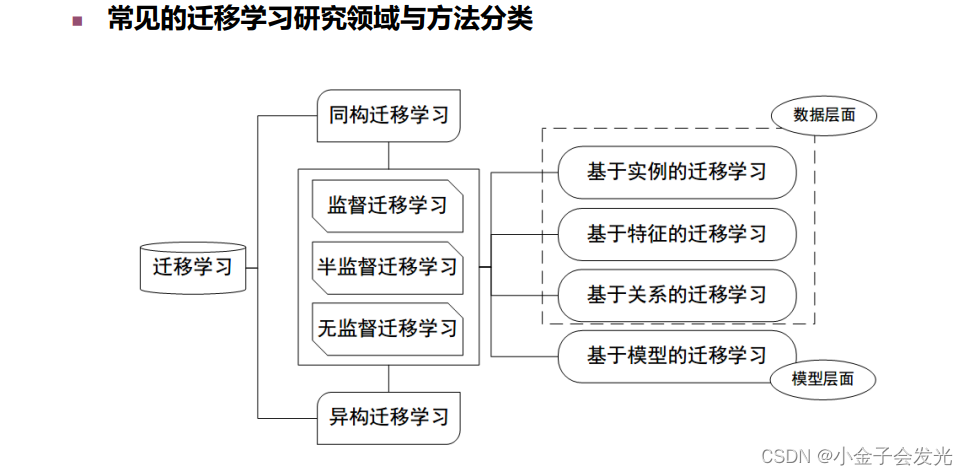
?图8?迁移学习的分类
3.1特征迁移
? ? ? ? 特征迁移学是寻找一个既可以代表源域特征又可以代表目标域特征的特征空间,达到通过源域的监督训练就可以提高目标领域分类性能的目的。在分类任务中,假设有大量训练数据分别为标记的源域数据和少量标记或未标记的目标域数据,这两个域的数据是相关领域不同场景的数据。特征迁移学习可以通过训练有标记的源域数据与未标记的目标域数据,以减少源域与目标域数据分布差异和提高源域的分类准确率为目标,进而去优化网络参数以达到更好的目标域分类。本文主要是基于特征迁移学习完成对轴承的跨域故障诊断。?
3.2微调迁移学习
? ? ? ?除了特征迁移外,还有一种常用的迁移学习方式,称为微调迁移学习。微调迁移学习是对参数的迁移,是指将源域中训练好的模型参数迁移到目标域中继续微调训练模型参数,实现源域的知识向目标域迁移。另外,微调迁移学习在图像分类中运用比较多,其具体流程是通过现有的大量图像训练得到网络的初始化参数,然后将初始化的网络迁移到目标域上,并利用目标域图像进行训练从而进一步微调优化网络权重参数,最终完成对目标域图像的分类。?
王晋东的迁移学习手册下载链接:
链接:https://pan.baidu.com/s/1f7VpJI7LaSXDP5EHV5CPRA?
提取码:jxu3?
--来自百度网盘超级会员V5的分享
?实验分析
? ? ? ?有了上面知识的基础以后,接下来就开始进行实验分析。具体实验参考的是如下的博客,近80块钱买的博客,买完就后悔了,感觉没实际用处。不过也因为这个,自己后面也找到了一篇比较不错的博客。
花了近80元买的博客如下:

 ?
?





?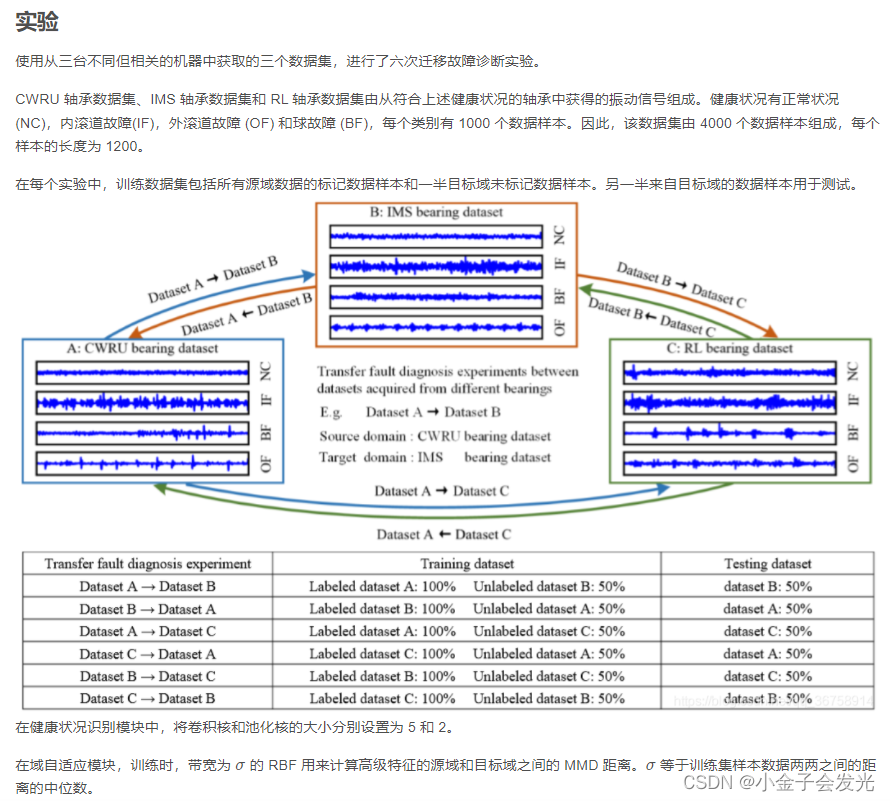
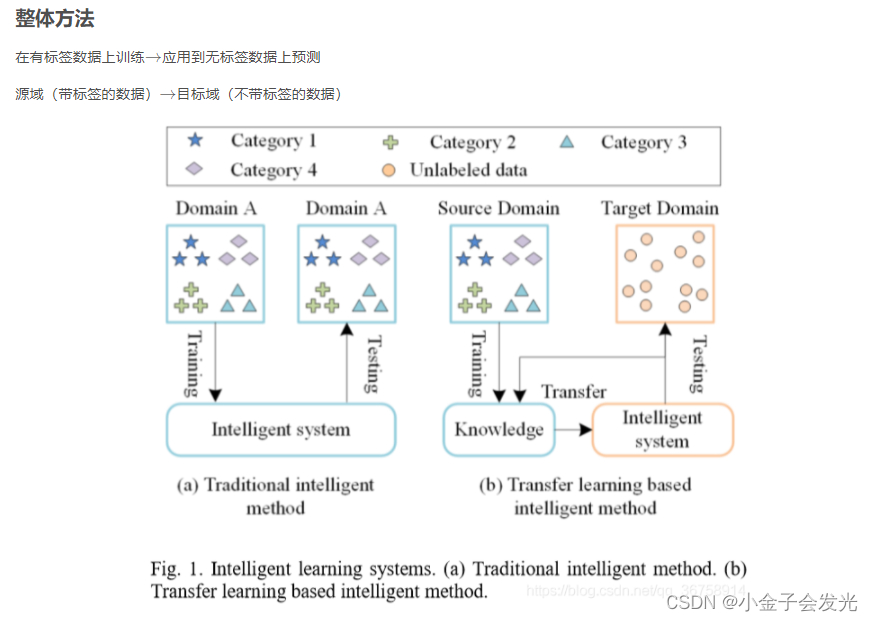
? ? ? ? 其实从上面的博客看下来,关键的东西就是损失函数,他这个损失函数是有三个部分组成,一个源域的分类损失函数,另一个是域判别器损失函数,最后一个源域和目标域的分布差异。
? ? ? ? 理解了这一点以后,其实剩下的就是如何去计算这三部分的损失函数,最后将三个损失函数进行线性组合,一般在域判别器损失函数、源域和目标域分布差异值这两部分前加上系数λ,u。另外还有一点就是域判别器损失函数是需要被减去。
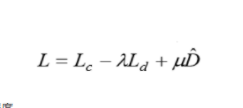
? ? ? ? ?如果损失函数部分看的不清楚,可以看一下下面推荐的一篇博客:
另一篇优质博客
? ? ? ? 理解了上面的内容以后,再提供一篇个人认为比较好的博客如下:
迁移学习-域分类损失函数-python代码实现_故障诊断与python学习的博客-CSDN博客_迁移学习python代码迁移学习-域分类损失函数-python代码讲解https://blog.csdn.net/m0_47410750/article/details/122915636? ? ? ?这一篇博客可以理解为是上面博客的测试案例,关键是有域判别器的损失函数代码。要做轴承迁移学习,这篇文章其实是个不错的开头,值得好好研究。
? ? ? ?我也就是简单引用其文章中的重点内容域判别器损失函数以及其如何嵌入到神经网络中,具体内容如下:
域判别器损失函数代码:
import torch
import torch.nn as nn
from torch.autograd import Function
import torch.nn.functional as F
import numpy as np
class LambdaSheduler(nn.Module):
def __init__(self, gamma=1.0, max_iter=1000, **kwargs):
super(LambdaSheduler, self).__init__()
self.gamma = gamma
self.max_iter = max_iter
self.curr_iter = 0
def lamb(self):
p = self.curr_iter / self.max_iter
lamb = 2. / (1. + np.exp(-self.gamma * p)) - 1
return lamb
def step(self):
self.curr_iter = min(self.curr_iter + 1, self.max_iter)
class AdversarialLoss(nn.Module):
'''
Acknowledgement: The adversarial loss implementation is inspired by http://transfer.thuml.ai/
'''
def __init__(self, gamma=1.0, max_iter=1000, use_lambda_scheduler=True, **kwargs):
super(AdversarialLoss, self).__init__()
self.domain_classifier = Discriminator()
self.use_lambda_scheduler = use_lambda_scheduler
if self.use_lambda_scheduler:
self.lambda_scheduler = LambdaSheduler(gamma, max_iter)
def forward(self, source, target):
lamb = 1.0
if self.use_lambda_scheduler:
lamb = self.lambda_scheduler.lamb()
self.lambda_scheduler.step()
source_loss = self.get_adversarial_result(source, True, lamb)
target_loss = self.get_adversarial_result(target, False, lamb)
adv_loss = 0.5 * (source_loss + target_loss)
return adv_loss
def get_adversarial_result(self, x, source=True, lamb=1.0):
x = ReverseLayerF.apply(x, lamb)
domain_pred = self.domain_classifier(x)
device = domain_pred.device
if source:
domain_label = torch.ones(len(x), 1).long()
else:
domain_label = torch.zeros(len(x), 1).long()
loss_fn = nn.BCELoss()
loss_adv = loss_fn(domain_pred, domain_label.float().to(device))
return loss_adv
class ReverseLayerF(Function):
@staticmethod
def forward(ctx, x, alpha):
ctx.alpha = alpha
return x.view_as(x)
@staticmethod
def backward(ctx, grad_output):
output = grad_output.neg() * ctx.alpha
return output, None
class Discriminator(nn.Module):
def __init__(self, input_dim=256, hidden_dim=256): #256是根据你的输入维度来修改的
super(Discriminator, self).__init__()
self.input_dim = input_dim
self.hidden_dim = hidden_dim
layers = [
nn.Linear(input_dim, hidden_dim),
nn.BatchNorm1d(hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim, hidden_dim),
nn.BatchNorm1d(hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim, 1),
nn.Sigmoid()
]
self.layers = torch.nn.Sequential(*layers)
def forward(self, x):
return self.layers(x)
? ? ? 其中有个部分需要修改:

? ? ? ? 如果你用其他卷积神经网络训练的话,需要确认最后你网络输出的结果是多少维度的,对应的将上面的256改成你所用网络输出的维度。比如说,我用VGG16模型训练,模型输入的图像为(16,512,512,3),按照十种故障类别,模型输出的结果是(16,10),也就是你输出的维度是10,需要把域判别器损失函数里面的256改成10即可。在训练的时候,自己也踩过雷,避免大家走弯路。
? ? ? 原作者利用该方法,进行了简单的测试,如下结果:
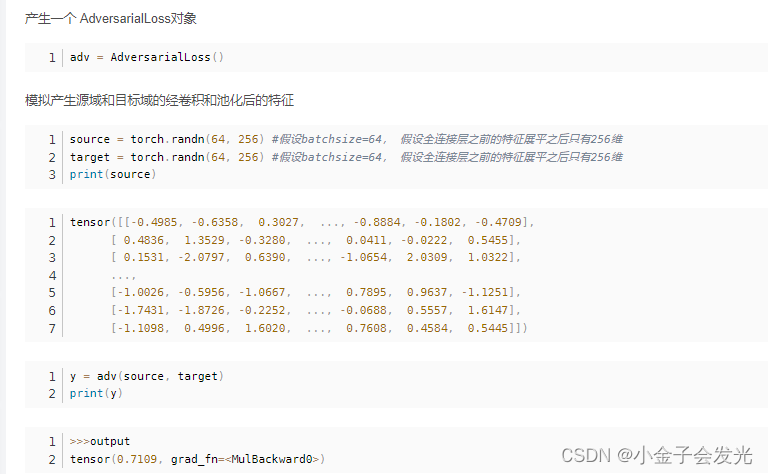
模型训练的流程:
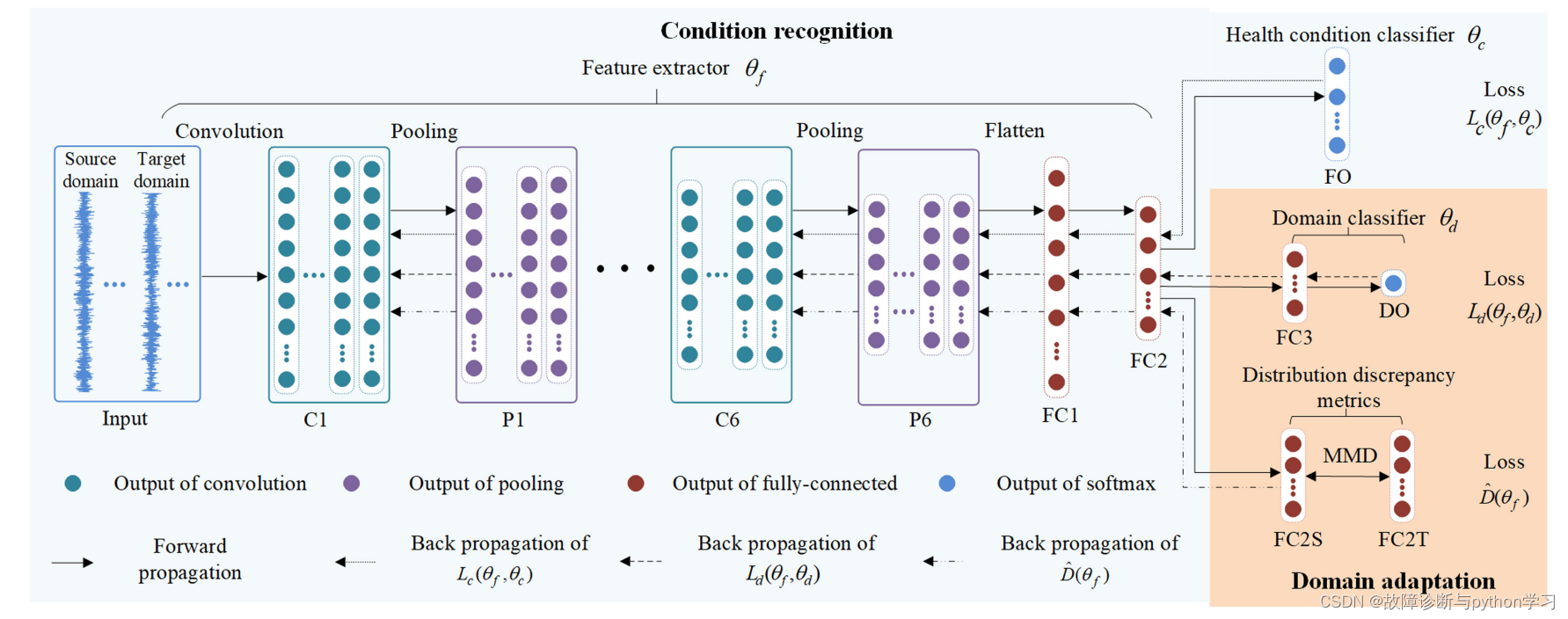
? ? ? ? 按照上面的模型思路,模型整体的训练如下所示。

? ? ? ? 上面的流程图上没有画上域判别器的损失函数部分,时间比较紧忘记画上去,导致下面的文章里面也没有写上去。实际实验中是加上去的。划分好训练集、测试集两部分。负载为0、负载为3的数据集,每个数据集一共1000张图片,按照4:1的比例划分,每个数据集中用于训练的数量为800张,用于测试的数量为200张

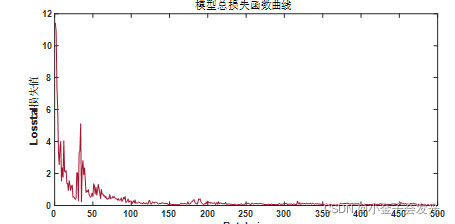
训练结果如下:
? ? ? ?利用tsne降维算法,对比分使用MK-MMD和不使用MK-MMD的区别。

?
?