机器学习知识简要总结
监督学习:给算法一个数据集,其中包含正确答案(有标记),数据集中的每个样本都给出正确答案,算法的目的是给出更多的正确答案。
无监督学习:对于给定的数据集,在未给出正确答案(无标记)的情况下将其分为不同的类,比如聚类算法。
回归:设法预测连续值的输出。
分类:预测离散值的输出。
线性回归:
拟合曲线Hypothesis:
y
=
θ
0
+
θ
1
x
y=\theta_0+\theta_1x
y=θ0?+θ1?x
平方误差代价函数Cost function:
J
(
θ
0
,
θ
1
)
=
1
2
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
?
y
(
i
)
)
2
J(\theta_0,\theta_1)=\frac{1}{2m} \sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2
J(θ0?,θ1?)=2m1?∑i=1m?(hθ?(x(i))?y(i))2,
m
m
m为点的个数,
y
i
y^i
yi为真实值,
y
(
x
i
)
y\left(x^i\right)
y(xi)表示函数值。
目标Goal:
m
i
n
J
(
θ
0
,
θ
1
)
min J(\theta_0,\theta_1)
minJ(θ0?,θ1?)
梯度下降法
θ
j
:
=
θ
j
?
α
?
?
θ
j
J
(
θ
0
,
θ
1
)
(
f
o
r
j
=
0
a
n
d
j
=
1
)
\theta_j:=\theta_j-\alpha\frac{\partial }{\partial \theta_j}J(\theta_0,\theta_1) \quad (for \quad j=0 \quad and \quad j=1)
θj?:=θj??α?θj???J(θ0?,θ1?)(forj=0andj=1)
α
\alpha
α表示学习率,用来控制梯度下降步子大小。先计算
θ
0
\theta_0
θ0?和
θ
1
\theta_1
θ1?,再同时更新
θ
0
\theta_0
θ0?和
θ
1
\theta_1
θ1?,不能先计算
θ
0
\theta_0
θ0?,再带回式子计算
θ
1
\theta_1
θ1?。
在梯度下降的过程中,当接近极值时,导数值会自动变的越来越小。
矩阵和向量
矩阵Matrix:行数×列数。
A
i
j
A_{ij}
Aij?:
i
t
h
i^{th}
ithrow,
j
t
h
j^{th}
jthcolumn
向量Vector:n×1 matrix
例:
h
θ
(
x
)
=
?
40
+
0.25
x
h_\theta(x) = -40+0.25x
hθ?(x)=?40+0.25x,x值:2 3 4 5
[
1
2
1
3
1
4
1
5
]
×
[
?
0.40
0.25
]
=
[
?
40
×
1
+
2
×
0.25
?
40
×
1
+
3
×
0.25
?
40
×
1
+
4
×
0.25
?
40
×
1
+
5
×
0.25
]
\begin{bmatrix} 1 & 2 \\ 1 & 3 \\ 1 & 4 \\ 1 & 5 \end{bmatrix} × \begin{bmatrix} -0.40 \\ 0.25 \end{bmatrix} = \begin{bmatrix} -40×1+2×0.25 \\ -40×1+3×0.25 \\ -40×1+4×0.25 \\ -40×1+5×0.25 \end{bmatrix}
?????1111?2345??????×[?0.400.25?]=??????40×1+2×0.25?40×1+3×0.25?40×1+4×0.25?40×1+5×0.25??????
矩阵乘法特征:
一般情况下,
A
×
B
≠
B
×
A
A×B \neq B×A
A×B?=B×A 。特殊:
A
×
I
=
I
×
A
=
A
A×I = I×A = A
A×I=I×A=A,
I
I
I为单位矩阵。
结合律
单位矩阵Identity Matrix:
I
n
×
n
I_{n×n}
In×n?例如:
[
1
0
0
1
]
\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}
[10?01?]
[
1
0
0
0
1
0
0
0
1
]
\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 &0 \\ 0 & 0 & 1 \end{bmatrix}
???100?010?001????
矩阵的逆运算:
A
A
?
1
=
A
?
1
A
=
I
AA^{-1}=A^{-1}A=I
AA?1=A?1A=I。
没有逆矩阵的矩阵叫做奇异矩阵,例如零矩阵。
矩阵转置Matrix Transpose:设
A
A
A是
m
×
n
m×n
m×n的矩阵,
B
=
A
T
B=A^T
B=AT,则
B
B
B为
n
×
m
n×m
n×m的矩阵,并且
B
i
j
=
A
i
j
B_{ij}=A_{ij}
Bij?=Aij?
多元线性回归:
多特征向量:
n
n
n = 特征个数,
x
(
i
)
x^{(i)}
x(i)表示第
i
i
i组特征向量,
x
j
(
i
)
x_j^{(i)}
xj(i)? = 第
i
i
i个特征向量的第
j
j
j个特征的值。
拟合函数Hypothesis:
h
θ
(
x
)
=
θ
T
x
=
h
θ
(
x
)
=
θ
0
+
θ
1
x
1
+
θ
2
x
2
+
.
.
.
+
θ
n
x
n
h_\theta(x)=\theta^Tx=h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+...+\theta_nx_n
hθ?(x)=θTx=hθ?(x)=θ0?+θ1?x1?+θ2?x2?+...+θn?xn?
参数Parameters:
θ
0
,
θ
1
,
.
.
.
,
θ
n
\theta_0,\theta1,...,\theta_n
θ0?,θ1,...,θn?
代价函数Cost Function:
J
(
θ
0
,
θ
1
,
.
.
.
,
θ
n
)
=
1
2
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
?
y
(
i
)
)
2
J(\theta_0,\theta_1,...,\theta_n)=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2
J(θ0?,θ1?,...,θn?)=2m1?∑i=1m?(hθ?(x(i))?y(i))2
特征缩放Feature Scaling:将特征值缩小到-1到1之间,目的是为了使梯度下降的收敛速度更快,迭代次数更少。
均值归一化Z-Score:将
x
i
x_i
xi?变为
x
i
?
μ
i
σ
\frac{x_i-\mu_i}{\sigma}
σxi??μi??,
σ
\sigma
σ为该特征的标准差。
正规方程Normal equation
X
X
X是一个
m
×
(
n
+
1
)
m×(n+1)
m×(n+1)的矩阵,m表示样本的个数,n表示特征个数,
y
y
y是一个m维的向量,则可通过式子:
θ
=
(
X
T
X
)
?
1
X
T
y
\theta=(X^TX)^{-1}X^Ty
θ=(XTX)?1XTy计算
θ
\theta
θ参数。
当
?
?
θ
j
J
(
θ
)
=
0
(
j
=
1
,
2
,
.
.
.
,
n
)
\frac{\partial}{\partial\theta_j}J(\theta)=0(j=1,2,...,n)
?θj???J(θ)=0(j=1,2,...,n)时,求出的n个参数
θ
j
\theta_j
θj?就是最合理的参数,即能使代价函数最小的参数。
正规方程与梯度下降法的区别:
正规方程不需要选择学习率,也不需要迭代,但是对于多特征来说计算量很大,比如当有上万个特征时。而梯度下降法需要选择学习率和多次迭代,但适合于多特征。
logistic回归
Sigmoid function/Logistic function:
g
(
z
)
=
1
1
+
e
?
z
g(z)=\frac{1}{1+e^{-z}}
g(z)=1+e?z1?只要z大于0,则g(z)就会大于0.5,预测值为1,小于0.5,预测值为0.
如何选择参数
θ
\theta
θ?假设
h
θ
(
x
)
=
1
1
+
e
?
θ
T
x
h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}}
hθ?(x)=1+e?θTx1?
代价函数:
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
{
?
l
o
g
(
h
θ
(
x
)
)
if?
y
=
1
?
l
o
g
(
1
?
h
θ
(
x
)
)
if?
y
=
0
Cost(h_\theta(x),y)=\begin{cases} -log(h_\theta(x)) &\text{if } y=1 \\ -log(1-h_\theta(x)) &\text{if } y=0 \end{cases}
Cost(hθ?(x),y)={?log(hθ?(x))?log(1?hθ?(x))?if?y=1if?y=0?
可简化为:
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
?
y
l
o
g
(
h
θ
(
x
)
)
?
(
1
?
y
)
l
o
g
(
1
?
h
θ
(
x
)
)
Cost(h_\theta(x),y)=-ylog(h_\theta(x))-(1-y)log(1-h_\theta(x))
Cost(hθ?(x),y)=?ylog(hθ?(x))?(1?y)log(1?hθ?(x))
过拟合问题
减少过拟合现象:
1、减少选取变量的数量:选取重要的变量。
2、正则化:保留所有特征变量,但是减少量级或参数\theta的大小。
正则化
正则化:修改代价函数中参数大小——在代价函数后面加一个正则化项,以缩小每一个参数。因为有正则化参数的存在,为了让代价函数最小化,必须让对应的参数尽可能的小甚至趋于0。
J
θ
0
,
θ
1
,
.
.
.
,
θ
n
)
=
1
2
m
[
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
?
y
(
i
)
)
2
+
λ
∑
j
=
1
m
θ
j
2
]
J\theta_0,\theta_1,...,\theta_n)=\frac{1}{2m}[\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum_{j=1}^{m}\theta_j^2]
Jθ0?,θ1?,...,θn?)=2m1?[∑i=1m?(hθ?(x(i))?y(i))2+λ∑j=1m?θj2?],不给
θ
0
\theta_0
θ0?添加项。如果正则化参数
λ
\lambda
λ太大,则会使代价函数的参数几乎接近于0,容易产生欠拟合现象。
线性回归正则化:
1.梯度下降:
θ
0
=
θ
0
?
α
1
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
?
y
(
i
)
)
x
0
i
\theta_0=\theta_0-\alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_0^{{i}}
θ0?=θ0??αm1?∑i=1m?(hθ?(x(i))?y(i))x0i?
θ
j
=
θ
j
(
1
?
α
λ
m
)
?
α
1
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
?
y
(
i
)
)
x
j
i
\theta_j=\theta_j(1-\alpha\frac{\lambda}{m})-\alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{{i}}
θj?=θj?(1?αmλ?)?αm1?∑i=1m?(hθ?(x(i))?y(i))xji?
2.正规方程(不要求掌握):
θ
=
(
X
T
X
+
λ
[
0
0
.
.
.
0
0
1
.
.
.
0
.
.
.
.
.
.
.
.
.
.
.
.
1
]
)
?
1
X
T
y
\theta=(X^TX+\lambda\begin{bmatrix} 0 & 0 &... &0 \\ 0 & 1 & ... & 0 \\ & & ... \\ ... & ... & ... & 1 \end{bmatrix} )^{-1}X^Ty
θ=(XTX+λ?????00...?01...?............?001??????)?1XTy计算
θ
\theta
θ参数。
当
?
?
θ
j
J
(
θ
)
=
0
(
j
=
1
,
2
,
.
.
.
,
n
)
\frac{\partial}{\partial\theta_j}J(\theta)=0(j=1,2,...,n)
?θj???J(θ)=0(j=1,2,...,n)
逻辑回归正则化:
代价函数:
J
(
θ
)
=
?
1
m
[
∑
i
=
1
m
y
(
i
)
l
o
g
(
h
θ
(
x
(
i
)
)
)
?
(
1
?
y
(
i
)
)
l
o
g
(
1
?
h
θ
(
x
(
i
)
)
)
]
+
λ
2
m
∑
j
=
1
n
θ
j
2
J(\theta)=-\frac{1}{m}[\sum_{i=1}^my^{(i)}log(h_\theta(x^{(i)}))-(1-y^{(i)})log(1-h_\theta(x^{(i)}))]+\frac{\lambda}{2m}\sum_{j=1}^{n}\theta_j^2
J(θ)=?m1?[∑i=1m?y(i)log(hθ?(x(i)))?(1?y(i))log(1?hθ?(x(i)))]+2mλ?∑j=1n?θj2?
卷积神经网络
前向传播:逻辑回归。
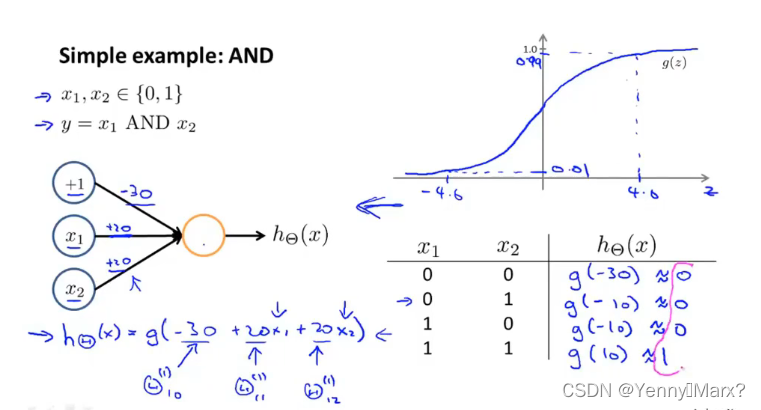
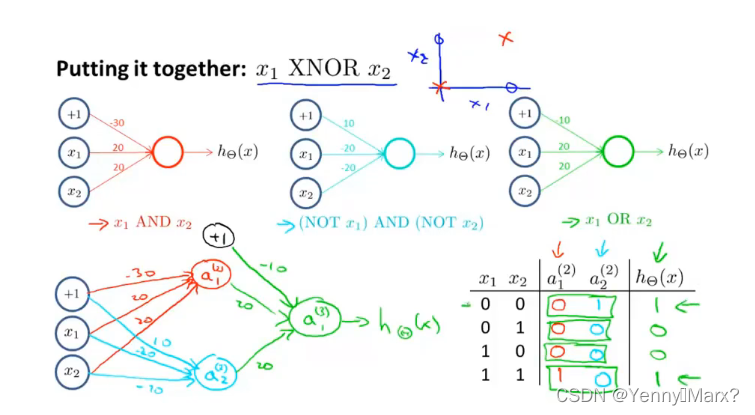
卷积神经网络中的代价函数:
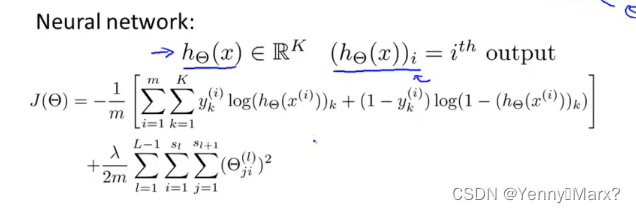
代价函数最小化:反向传播Backpropagation
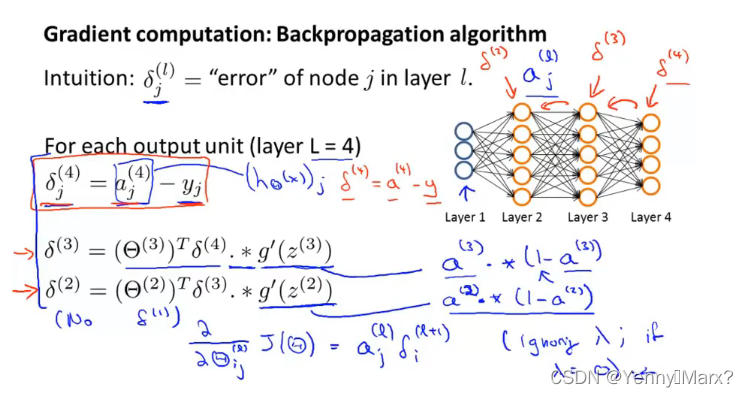

总误差对权重求偏导
 注意!!不懂可以看这篇文章:https://blog.csdn.net/weixin_38347387/article/details/82936585
注意!!不懂可以看这篇文章:https://blog.csdn.net/weixin_38347387/article/details/82936585
卷积神经网络训练步骤:
1.随机初始化权重,通常把权重初始化为很小的值,接近于0。
2.执行前向传播算法。
3.计算代价函数。
4.反向传播。
5.使用梯度检查比较已经计算得到的偏导数项,将反向传播得到的篇导数值与用数值方法得到的估计值进行比较。
6.用梯度下降算法或者更高级的优化算法和反向传播算法进行结合,来最小化代价函数。
模型选择和训练、验证、测试集
一般来说,60%训练集、20%验证、20%测试,训练集用来训练每个模型,验证集用来选择模型,测试集用来评估泛化误差,相当于学习、模拟考、高考的关系。
评价指标
准确率(Accuracy) = (TP + TN) / 总样本,
精确率(Precision) = TP / (TP + FP)
召回率(Recall) = TP / (TP + FN)
无监督学习
K-means:随机生成两点(聚类中心),遍历每个数据,看该数据和哪个聚类中心近,就分到哪一类。所有数据点都测过后,找到每一类的均值中心,将聚类中心移到均值中心,再重新开始新一轮的归类,直到每个点到该点所属的 聚类中的距离平方和最小。
选择聚类中心的个数:肘部法则
主成分分析
主成分分析(PCA):找一个投影平面,对数据进行投影,使得数据点到投影面的垂直距离最小。在PCA之前,先对数据进行归一化和标准化,使得数据的均值为0,且在合适的范围内。PCA也可用于降维。
PCA与线性回归不同的是:PCA是数据点到直线的垂直距离(是倾斜的),线性回归是数据点到直线的距离。