深度学习之损失函数小结
开篇
损失函数在深度学习中的作用相当于引领模型学习的方式,其重要程度不言而喻;
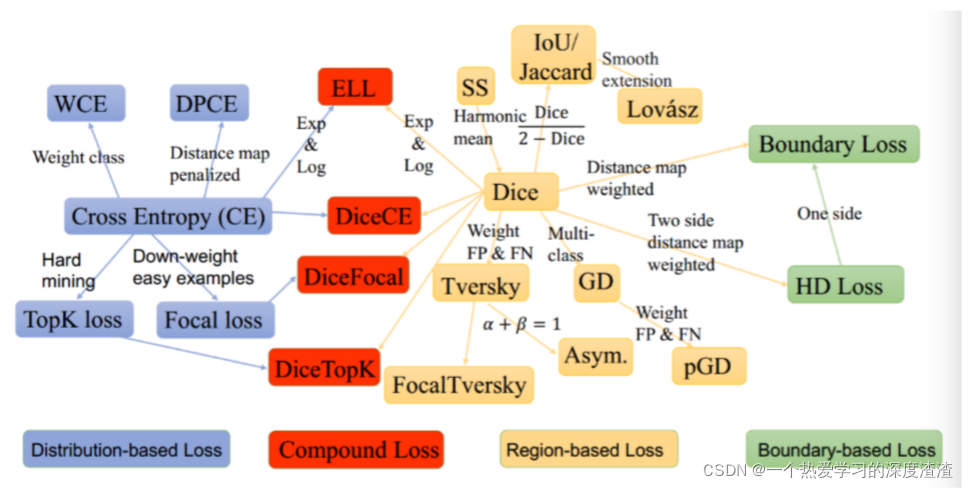
下图为一些损失函数的关系:
Sigmoid和Softmax损失
Sigmoid公式: S ( x ) = 1 1 + e ? x S(x)=\frac{1}{1+e^{-x}} S(x)=1+e?x1?
Softmax公式: S ( x j ) = e x j ∑ k = 1 K e x k , j = 1 , 2 , … , K S\left(x_{j}\right)=\frac{e^{x_{j}}}{\sum_{k=1}^{K} e^{x_{k}}}, j=1,2, \ldots, K S(xj?)=∑k=1K?exk?exj??,j=1,2,…,K
二者的区别:
-
sigmoid作用于输出为非互斥类别,且可以同时选择多个类别;
-
Softmax作用于输出为互斥类别,且只能选择一个类别;
交叉熵损失函数
Binary Cross Entropy,最基本的交叉熵损失函数形式(二分类交叉熵)
公式: L = ? ∑ c = 1 M y c log ? ( p c ) L=-\sum_{c=1}^{M} y_{c} \log \left(p_{c}\right) L=?∑c=1M?yc?log(pc?)
但由于任务的数据往往不均衡,可采用加权交叉熵损失或者平衡交叉熵损失的方式;
Focal Loss
也是一种交叉熵损失函数的变形
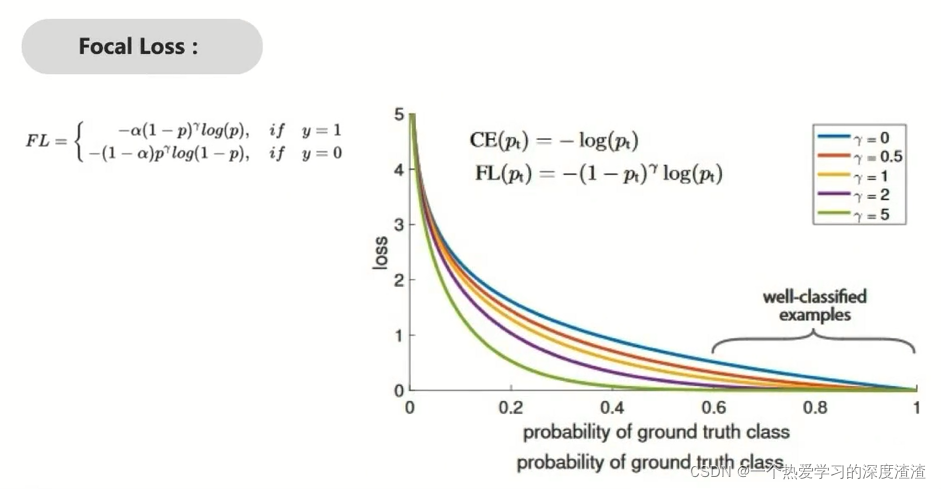
其中有两个超参数,都是为了解决一定问题;
α:正负样本不均衡的问题,相当于加了权重;
γ:解决困难样本,相当于加重对困难样本的惩罚;
L1 Loss和L2 Loss
均方误差MSE(L2 Loss)计算公式: M S E = ∑ i = 1 n ( f x i ? y i ) 2 n M S E=\frac{\sum_{i=1}^{n}\left(f_{x i}-y_{i}\right)^{2}}{n} MSE=n∑i=1n?(fxi??yi?)2?
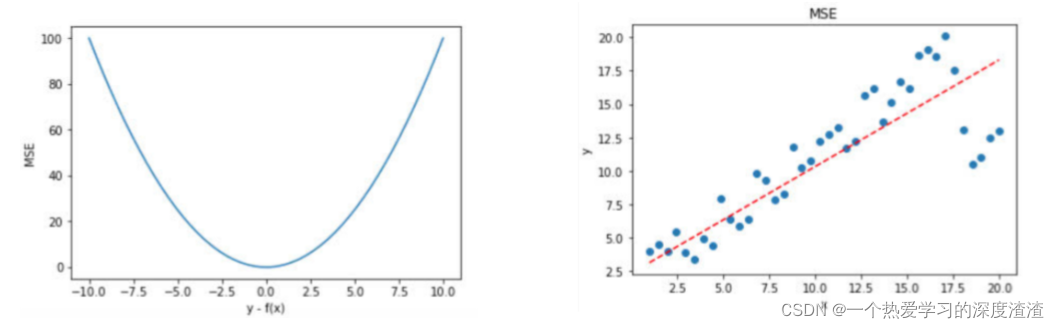
存在问题:
1、容易受离群点影响;
2、由于梯度没有上限,容易产生梯度爆炸;
平均绝对误差MAE(L1 Loss)计算公式: M A E = ∑ n = 1 n ∣ f ( x i ) ? y i ∣ n M A E=\frac{\sum_{n=1}^{n}\left|f\left(x_{i}\right)-y_{i}\right|}{n} MAE=n∑n=1n?∣f(xi?)?yi?∣?
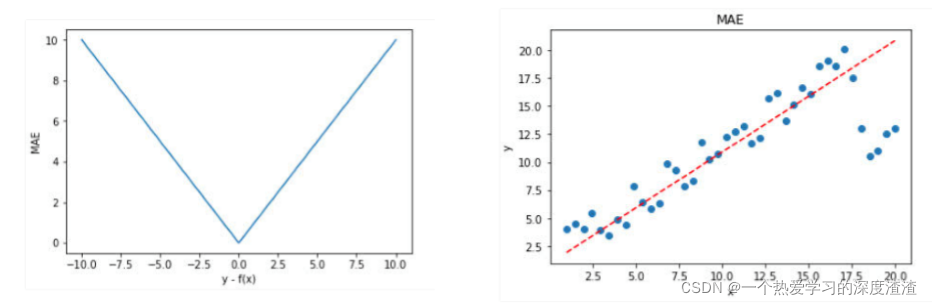
存在问题:虽然受离群点的影响较少,但梯度一直不变,不利于模型收敛
L1 Loss的改进版:Smooth L1 Loss:
计算公式:
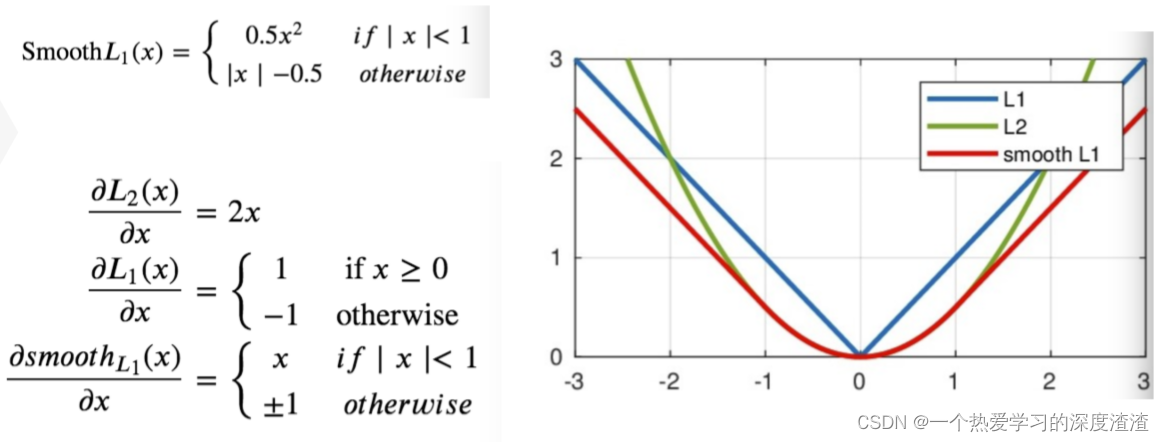
说明:在【-1,1】这个区间内,和L2 Loss是很接近的,在其余区域和L1 Loss接近;也就是结合二者的优点,一开始收敛较快,后续又能慢慢收敛;
为什么分类问题损失函数用交叉熵而不是MSE
首先从损失函数的梯度上理解:
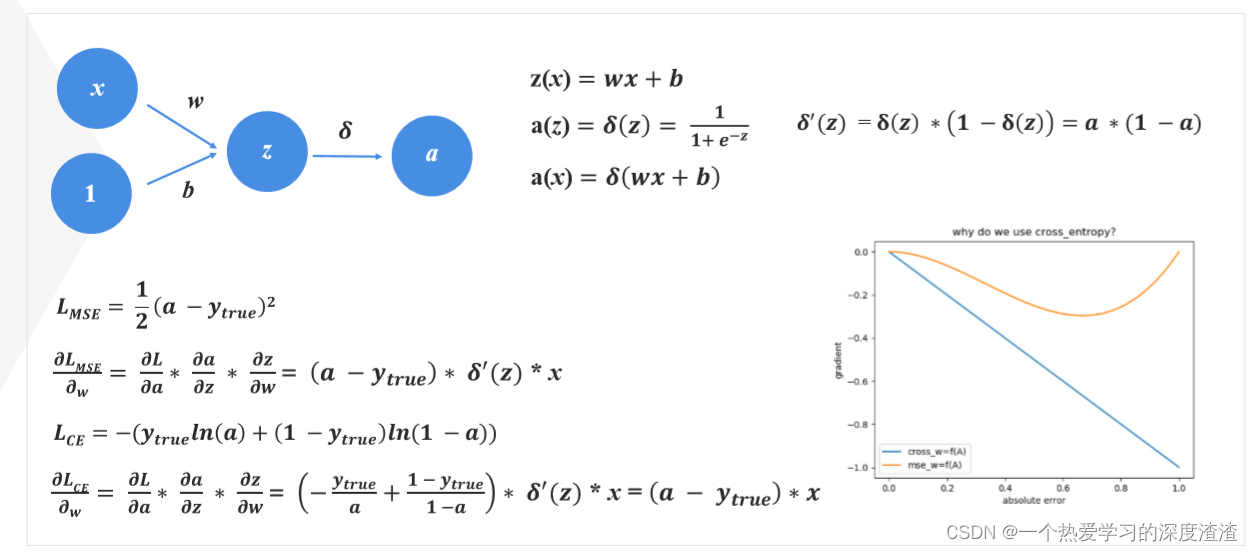
可以看出,MSE会出现梯度消失的情况,在过小和过大的值时;
而且,分类问题只关注置信度最大的类别,对于其他类别并不关心,而MSE损失会优化所有输出;
Dice Loss
首先看一下Dice系数的计算公式,实际上和IOU很相似
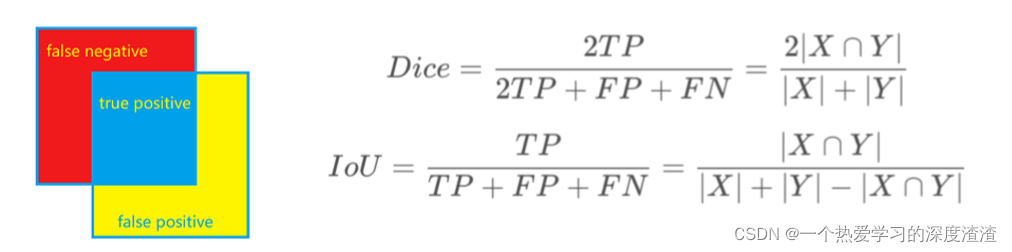
转换公式可以写成:IoU = Dice / 2 - Dice
待补充