文章目录
图片加密的评价指标—直方图统计与熵值
- 本篇文章对加密(置乱)后的图像进行评估,采用matlab来计算加密前后的图像直方图统计,以及图像的熵值。
- 灰度直方图统计能反映一幅图的像素分布,或者说是亮度变化,针对加密图像来说,通过直方图统计可得到像素之间的 相关性 关系。
- 图像熵值能反映图像的平均信息量,同时熵值越大,说明图像越混乱。
根据以上,我们对FPGA实现加密后的图像进行质量评估。
1、首先给出原图与加密后的图像
2、matlab进行直方图统计:
I = imread('his22.png') ; % 读取rgb图像
I = rgb2gray(I);
figure, imshow(I);
figure, imhist(I); % 显示图像的灰度值直方图
结果如下:
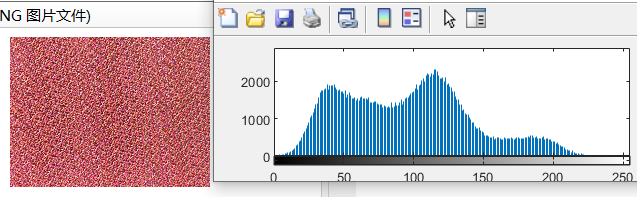

通过上述图片可看出,加密后的图像分布更均匀,且直方图统计特性不如原图明显,因此说明图像像素之间的相关性低,也就是图像越混乱,从而达到了加密的效果。
3、同样对原图与加密图进行图像熵值的计算
clc
clear
close all
I=imread('his22.png');
[C,L]=size(I); %求图像的规格
Img_size=C*L; %图像像素点的总个数
G=256; %图像的灰度级
H_x=0;
nk=zeros(G,1);%产生一个G行1列的全零矩阵
for i=1:C
for j=1:L
Img_level=I(i,j)+1; %获取图像的灰度级
nk(Img_level)=nk(Img_level)+1; %统计每个灰度级像素的点数
end
end
for k=1:G %循环
Ps(k)=nk(k)/Img_size; %计算每一个像素点的概率
if Ps(k)~=0 %如果像素点的概率不为零
H_x=-Ps(k)*log2(Ps(k))+H_x; %求熵值的公式
end
end
在命令行输入如下指令,即可求出熵值
H_x %显示熵值
通过计算可知,原图熵值为7.71,加密图的熵值为7.84,因此加密后的图像熵值更大,同时对于8位的灰度图来说,最大的信息熵值是8,7.84更接近于8,说明加密后图像的混乱程度大。
补充:加密后的直方图统计以及熵值虽然能说明加密成功,但是为了带来更好的效果,可增加置乱变换的次数,但是不可违背置乱的周期性,也就是在可复原的周期内,最大限度的变换图像,从而即可得到更好的加密效果。
参考:
https://blog.csdn.net/qq_44420246/article/details/100594343