[人工智能]opencv--图像处理

1. 图像的几何变换

1.1 图像缩放

缩放是针对图像进行大小调整，即图像放大或缩小
APIcv2.resize(src,dsize,fx=0,fy=0,interpolation=cv2.INTER_LINEAR)

参数：

• src：输入的图像
• dsize：绝对尺寸，直接指定调整后图像的大小，为一二维元组（cols， rows），注：图像的shape前两维为（rows，cols）
• fx,fy为相对尺寸，注需将dsize设置为None，fx和fy为比例因子
• interpolation：插值方法
  • cv2.INTER_NEAREST - 最邻近插值
  • cv2.INTER_LINEAR - 双线性插值，如果最后一个参数你不指定，默认使用这种方法
  • cv2.INTER_AREA
  • cv2.INTER_CUBIC - 4x4像素邻域内的双立方插值
  • cv2.INTER_LANCZOS4 - 8x8像素邻域内的Lanczos插值

注意事项：

• dsize和fx/fy不能同时为0
• 插值方法，正常情况下使用默认的双线性插值就够用了。
• 几种常用方法的效率是：最邻近插值>双线性插值>双立方插值>Lanczos插值；但是效率和效果成反比，所以根据自己的情况酌情使用。
• 通常情况下，dst（输出图像）的大小和类型是未知的，类型是有src（原图像）继承而来的，大小是根据参数计算而来的。但加入已知dst的大小，可采用如下方式dst = cv2.resize(src, dst.size(), 0, 0, interpolation)

import cv2 as cv
# 1. 读取图片
img1 = cv.imread("./image/dog.jpeg")
# 2.图像缩放
# 2.1 绝对尺寸
rows,cols = img1.shape[:2]
res = cv.resize(img1,(2*cols,2*rows),interpolation=cv.INTER_CUBIC)

# 2.2 相对尺寸
res1 = cv.resize(img1,None,fx=0.5,fy=0.5)

# 3 图像显示
# 3.1 使用opencv显示图像(不推荐)
cv.imshow("orignal",img1)
cv.imshow("enlarge",res)
cv.imshow("shrink）",res1)
cv.waitKey(0)

# 3.2 使用matplotlib显示图像
fig,axes=plt.subplots(nrows=1,ncols=3,figsize=(10,8),dpi=100)
axes[0].imshow(res[:,:,::-1])
axes[0].set_title("绝对尺度（放大）")
axes[1].imshow(img1[:,:,::-1])
axes[1].set_title("原图")
axes[2].imshow(res1[:,:,::-1])
axes[2].set_title("相对尺度（缩小）")
plt.show()

1.2 图像平移

将图像按照指定方向和距离，移动到相应的位置
API:cv2.warpAffine(img, M, dsize)
参数：

• img：输入图像
• M：为一2×3的矩阵，例如对于$(x,y)$处的像素点，把它移动到$(x+t_x,y+t_y)$处时，M矩阵应设置为：
  $$M=\left|\begin{array}{ccc}1& 0& t_x\\ 0& 1& t_y\end{array}\right|$$
• dsize:输出图像的大小，（cols， rows）

import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt
# 1. 读取图像
img1 = cv.imread("./image/image2.jpg")

# 2. 图像平移
rows,cols = img1.shape[:2]
M = M = np.float32([[1,0,100],[0,1,50]])# 平移矩阵
dst = cv.warpAffine(img1,M,(cols,rows))

# 3. 图像显示
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,8),dpi=100)
axes[0].imshow(img1[:,:,::-1])
axes[0].set_title("原图")
axes[1].imshow(dst[:,:,::-1])
axes[1].set_title("平移后结果")
plt.show()

1.3 图像旋转

将图像依据某个位置并按照一定角度进行转动的过程，旋转过程中图像仍然保持原本尺寸。
图像旋转后图像的水平对称轴、垂直对称轴及中心坐标原点都可能会发生变换，因此需要对图像旋转中的坐标进行相应转换。
图像如何进行旋转：

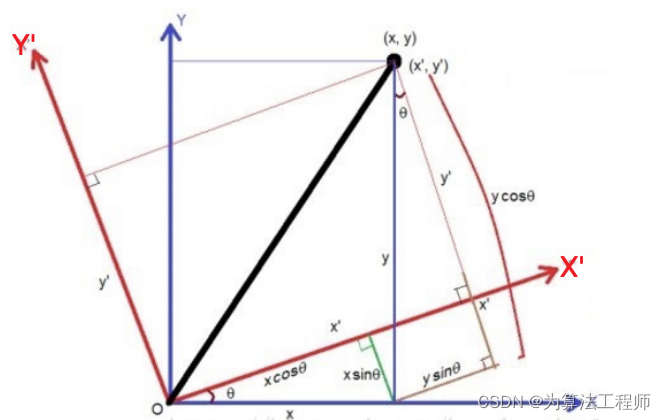
假设图像逆时针旋转$\theta$,则根据坐标转变可得旋转转换为：
$$\{\begin{array}{l}{x}^{{}^{\prime }}=rcos(\alpha ?\theta )\\ y^{{}^{\prime }}=rsin(\alpha ?\theta )\end{array}$$
其中：
$$r=\sqrt{x^2+y^2}，sin\alpha =\frac{y}{\sqrt{x^2+y^2}},cos\alpha =\frac{x}{\sqrt{x^2+y^2}}$$
则会有：
$$[x^{{}^{\prime }}{y}^{{}^{\prime }}1]=[xy1]\left|\begin{array}{ccc}cos\theta & ?sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right|$$
即：
$$\{\begin{array}{l}{x}^{{}^{\prime }}=xcos\theta +ysin\theta \\ y^{{}^{\prime }}=?xsin\theta +ycos\theta \end{array}$$
图像在旋转完成后，还需要修正原点的位置，因为原图像中的坐标原点在图像的左上角，经旋转后的图像的大小会有所变换，需要进行原点修正。

假设在旋转时，是以旋转中心为坐标原点的，那么旋转结束后还需要将坐标原点移动到图像左上角，即还需要进行一次变换。
$$[x^{{}^{\prime \prime }}{y}^{{}^{\prime \prime }}1]=[x^{{}^{\prime }}{y}^{{}^{\prime }}1]\left|\begin{array}{ccc}1& 0& 0\\ 0& ?1& 0\\ left& top& 1\end{array}\right|=[xy1]\left|\begin{array}{ccc}cos\theta & ?sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right|\left|\begin{array}{ccc}1& 0& 0\\ 0& ?1& 0\\ left& top& 1\end{array}\right|$$
opencv中图像旋转首先根据旋转角度和旋转中心获取旋转矩阵，然后根据旋转矩阵进行变换，即可实现任意角度和任意中心的旋转效果。
获取旋转矩阵API：cv2.getRotarionMatrix2D(center, angle, scale)
参数：

• center：旋转中心
• angle：旋转角度
• scale：缩放比列
  返回值为 M：旋转矩阵
  进行旋转变换API：cv.warpAffine(img,M,(cols,rows))
  参数：
• img：要旋转的图像
• M：旋转矩阵
• （cols，rows）：平移后图像尺寸

import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt
# 1 读取图像
img = cv.imread("./image/image2.jpg")

# 2 图像旋转
rows,cols = img.shape[:2]
# 2.1 生成旋转矩阵
M = cv.getRotationMatrix2D((cols/2,rows/2),90,1)
# 2.2 进行旋转变换
dst = cv.warpAffine(img,M,(cols,rows))

# 3 图像展示
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,8),dpi=100)
axes[0].imshow(img1[:,:,::-1])
axes[0].set_title("原图")
axes[1].imshow(dst[:,:,::-1])
axes[1].set_title("旋转后结果")
plt.show()

1.4 仿射变换

图像的仿射变换设计到图像的形状、位置和角度的变换，是深度学习预处理常用的功能，仿射变换主要是对图像的缩放、旋转、翻转和平移等操作的组合。
opencv中，仿射变换矩阵是一个2×3的矩阵：
$$M=[AB]=\left|\begin{array}{ccc}{a}_{00}& a_{01}& b_0\\ a_{10}& a_{11}& b_1\end{array}\right|$$
其中左边的2×2子矩阵$A$是线性变换矩阵，右边的2×1子矩阵$B$是平移项：
$$A=\left|\begin{array}{cc}{a}_{00}& a_{01}\\ a_{10}& a_{11}\end{array}\right|,B=\left|\begin{array}{c}{b}_0\\ b_1\end{array}\right|$$
对于图像上的任一位置$(x,y)$，仿射变换执行的是如下的操作：
$$T_{affine}=A\left|\begin{array}{c}x\\ y\end{array}\right|+B=M\left|\begin{array}{c}x\\ y\\ 1\end{array}\right|$$
注：对于图像而言，宽度方向是x，高度方向是y，坐标的顺序和图像像素对应下标一致。那么原点的位置不是左下角而是右上角，y的方向也不是向上而是向下。
在仿射变换中，原图中所有的平行线在结果图像中同样平行。为得到仿射变换矩阵M，需要从原图像中找到三个点以及他们在输出图像中的位置，然后利用API：cv2.getAffineTransform(pts1, pts2)
参数pts1和pts2分别是原图和输出图的对应点（pts1仿射变换后即为pts2）
仿射变换API：cv2.warpAffine(img, M, (cols, rows))

import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt
# 1 图像读取
img = cv.imread("./image/image2.jpg")

# 2 仿射变换
rows,cols = img.shape[:2]
# 2.1 创建变换矩阵
pts1 = np.float32([[50,50],[200,50],[50,200]])
pts2 = np.float32([[100,100],[200,50],[100,250]])
M = cv.getAffineTransform(pts1,pts2)
# 2.2 完成仿射变换
dst = cv.warpAffine(img,M,(cols,rows))

# 3 图像显示
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,8),dpi=100)
axes[0].imshow(img[:,:,::-1])
axes[0].set_title("原图")
axes[1].imshow(dst[:,:,::-1])
axes[1].set_title("仿射后结果")
plt.show()

1.5 透射变换

透射变换是视角变换的结构，是指利用透视中心、像点、目标点三点共线的条件，按照透视旋转定律使承影面（透视面）绕迹线（透视轴）旋转某一角度，破坏原有的投影光线束，仍能保持承影面上投影几何图形不变的变换。
其本质为将图像投影到一个新的视平面，其通用变换公式为：
$$[x_{{}^{\prime }}{y}_{{}^{\prime }}{z}_{{}^{\prime }}]=[uvw]\left|\begin{array}{ccc}{a}_{00}& a_{01}& a_{02}\\ a_{10}& a_{11}& a_{12}\\ a_{20}& a_{21}& a_{22}\end{array}\right|$$
其中，$(u,v)$是原始的图像像素坐标，$w$取值为1.
$(x=x^{{}^{\prime }}/z^{{}^{\prime }},y=y^{{}^{\prime }}/z^{{}^{\prime }})$是透射变换后的结果。后面的矩阵称为透视变换矩阵，一般情况下将其分为三部分：
$$T=\left|\begin{array}{ccc}{a}_{00}& a_{01}& a_{02}\\ a_{10}& a_{11}& a_{12}\\ a_{20}& a_{21}& a_{22}\end{array}\right|=\left|\begin{array}{cc}{T}_1& T_2\\ T_3& a_{22}\end{array}\right|$$
其中，$T_1$表示对图像进行线性变换，$T_2$对图像进行平移，$T_3$表示对图像进行投射变换，$a_{22}$一般设为1
在opencv中，需要找到四个点，其中任意三个不共线，之后通过APIcv.getPerspectiveTransform找到变换矩阵T，透射变换APIcv.warpPerspective

import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt
# 1 读取图像
img = cv.imread("./image/image2.jpg")
# 2 透射变换
rows,cols = img.shape[:2]
# 2.1 创建变换矩阵
pts1 = np.float32([[56,65],[368,52],[28,387],[389,390]])
pts2 = np.float32([[100,145],[300,100],[80,290],[310,300]])

T = cv.getPerspectiveTransform(pts1,pts2)
# 2.2 进行变换
dst = cv.warpPerspective(img,T,(cols,rows))

# 3 图像显示
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,8),dpi=100)
axes[0].imshow(img[:,:,::-1])
axes[0].set_title("原图")
axes[1].imshow(dst[:,:,::-1])
axes[1].set_title("透射后结果")
plt.show()

1.6 图像金字塔

图像金字塔是图像多尺度表达的一种，最主要用于图像的分割，是一种以多分辨率来解释图像的有效但概念简单的结构。
图像金字塔用于机器视觉和图像压缩，一幅图像的金字塔是一系列以金字塔形状排列的分辨率逐步降低且来源同一张原始图像的图像集合。其通过梯次向下采样获得，直到达到某个终止条件才停止采样。
金字塔的底部是待处理图像的高分辨率表示，而顶部是低分辨率的近似，层级越高，图像越小，分辨率越低。
上采样API：cv2.pytUp(img)；下采样API：cv2.pyrDown(img)

import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt
# 1 图像读取
img = cv.imread("./image/image2.jpg")
# 2 进行图像采样
up_img = cv.pyrUp(img)  # 上采样操作
img_1 = cv.pyrDown(img)  # 下采样操作
# 3 图像显示
cv.imshow('enlarge', up_img)
cv.imshow('original', img)
cv.imshow('shrink', img_1)
cv.waitKey(0)
cv.destroyAllWindows()