目录
一、公式

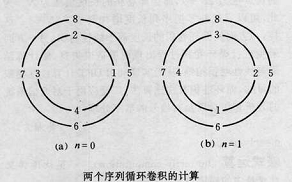
 ?
?
?特点:假设序列1长度N,序列2长度N,则循环卷积结果长度依旧为N
二、代码
方法一:遍历
# 循环卷积
def cc(x1,x2):
# 计算两个列表的对应元素乘积之和
def sum_(x1,x2):
sumV = 0
for i in range(len(x1)):
sumV += x1[i]*x2[i]
return sumV
N = len(x1) # 共4步
x0 = [0 for _ in range(N)]
X = []
for i in range(N):
sumV = sum_(x1,x2)
x0[i] = sumV
X.append(x0[:])
x1 = [x1[-1]] + x1[:-1]
return X
if __name__ == '__main__':
x = [1,1,1,1]
y = [4,3,2,1]
print(cc(x,y))[[10,0,0,0],[10,10,0,0].[10,10,10,0],[10,10,10,10]]?
方法二:利用卷积定理
![]()
1、先求两个序列的DFT变换序列;
2、求DFT变换后的序列之积;
3、对序列之积拟傅里叶变换IDFT
def synthesis_matrix(N):
ts = np.arange(N) / N
freqs = np.arange(N)
args = np.outer(ts, freqs)
M = np.exp(1j * PI2 * args)
return M
def dft(ys):
N = len(ys)
M = synthesis_matrix(N)
amps = M.conj().transpose().dot(ys)
return amps
def idft(amps):
N = len(amps)
M = synthesis_matrix(N)
ys = M.dot(amps) / N
return ys原序列?
?
DFT变换?
 ?
?
DFT变换后序列乘积?
?
逆傅里叶变换IDFT?
 ?
?
?