[人工智能]lagrange插值法、多项式插值法习题---python实践

1.等分点、lagrange插值法
lagrange算法实现参考我的 拉格朗日差值法python实现 文章
b站视频教程：https://www.bilibili.com/video/BV14Z4y1z78B?share_source=copy_web

import numpy
import matplotlib
import math
from matplotlib import pyplot
import time
N=10   #N=100时会发生lunge现象
pi=math.pi  #引入pi常量
x=[]
y=[]
time1=time.time()
for i in range(N):
    x.append(round((-1+(2/N)*(N-i)),3))

def function(x1):
    return math.sin(pi*x1)

for i in range(len(x)):
    y.append(function(x[i]))


def lagrange_interploate(x1):
    P=[]
    L_n=0
    for i in range(len(x)):
        numerator=1
        denominator=1
        for j in range(len(x)):
            if j!=i:
                numerator*=(x1-x[j])
                denominator*=(x[i]-x[j])
        P.append(numerator/denominator)

    for i in range(len(x)):
        L_n+=y[i]*P[i]

    return round(L_n,3)
x1=[]
y1=[]  #lagrange估值
y2=[]  #真实值
for i in range(1000):
    x1.append(round((-1 + (2 / 1000) * (1000 - i)), 3))   #生成1000个横坐标
for i in range(1000):
    y1.append(lagrange_interploate(x1[i]))   #调用1000次lagrange函数，计算对应y1[i]的估值
for i in range(1000):
    y2.append(function(x1[i]))  #调用1000次sin(pi*x)函数，计算对应纵坐标的真实值
time2=time.time()

pyplot.plot(x1,y1)
# pyplot.scatter(x1,y1,marker='.')
pyplot.show()

#计算误差
error=[]
for i in range(1000):
    error.append(abs(y1[i]-y2[i]))

print("耗时：",time2-time1)
print(max(error))

结果：

耗时： 0.01949167251586914
0.0005494680508606742

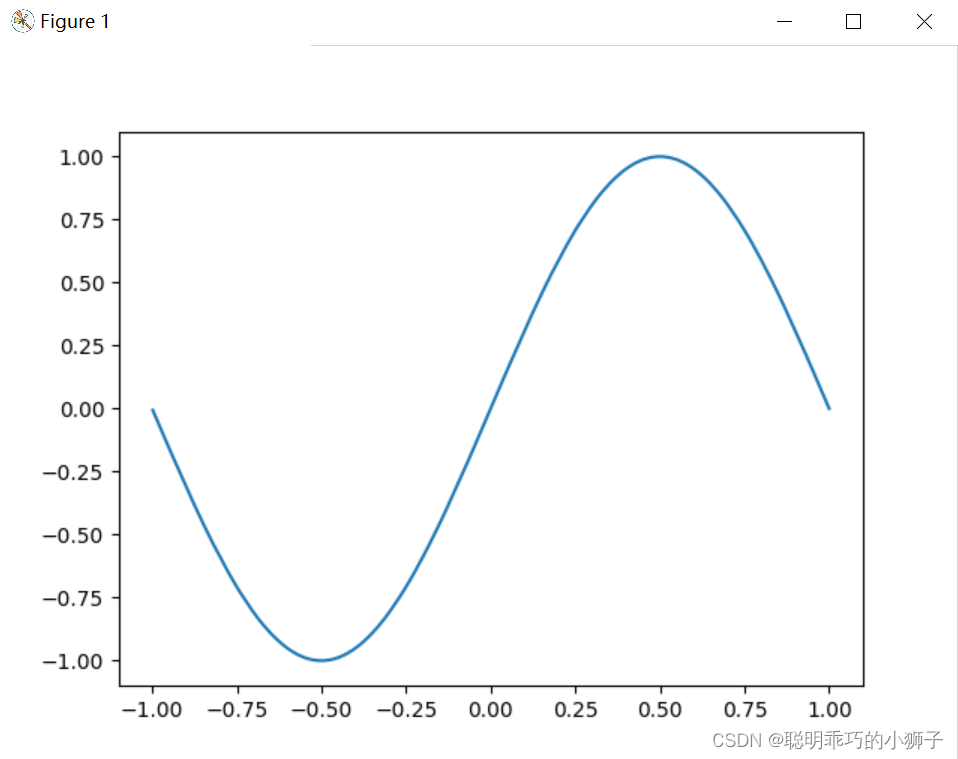
2.非等分点（切比雪夫高斯巴托点）、lagrange插值法
将

for i in range(N):
    x.append(round((-1+(2/N)*(N-i)),3))

改为

for i in range(N):
    x.append(math.cos(i*pi/N))

即可
结果：

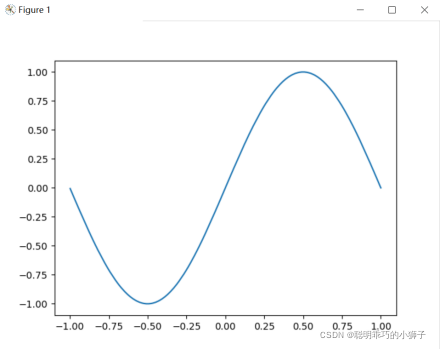
3.等分点，多项式插值
多项式插值算法见我的多项式插值算法python实现

import numpy as np
from numpy import *
import matplotlib
from matplotlib import pyplot
import time
import numpy.linalg as lg    #numpy的线性代数函数库 linalg
import math
time1=time.time()
x=[]
y=[]
N=10
pi=math.pi
for i in range(N):
    x.append(round((-1+(2/N)*(N-i)),3))

def function(x1):
    return math.sin(pi*x1)

for i in range(len(x)):
    y.append(function(x[i]))
print(x)
n = len(x)
X= zeros((n, n))
for i in range(n):
    for j in range(n):
        X[i][j] = math.pow(x[i],j)
print(X)    #范德蒙
A=[]    #系数矩阵
XT=lg.inv(X)
Y=zeros((n,1))
for i in range(len(y)):
    Y[i][0]=y[i]

A=lg.solve(X,Y)
def polynomial_interploate(x1):
    P=0
    for i in range(len(x)):
        P+=A[i][0]*math.pow(x1,i)
    return P

x1=[]
y1=[]  #lagrange估值
y2=[]  #真实值
for i in range(1000):
    x1.append(round((-1 + (2 / 1000) * (1000 - i)), 3))   #生成1000个横坐标
for i in range(1000):
    y1.append(polynomial_interploate(x1[i]))   #调用1000次多项式插值函数，计算对应y1[i]的估值
for i in range(1000):
    y2.append(function(x1[i]))  #调用1000次sin(pi*x)函数，计算对应纵坐标的真实值

time2=time.time()
pyplot.plot(x1,y1)
# pyplot.scatter(x1,y1,marker='.')
pyplot.show()


#计算误差
error=[]
for i in range(1000):
    error.append(abs(y1[i]-y2[i]))

print("耗时：",time2-time1)
print("误差：",max(error))

结果：

耗时： 0.013129234313964844
误差： 5.1646154663520516e-05

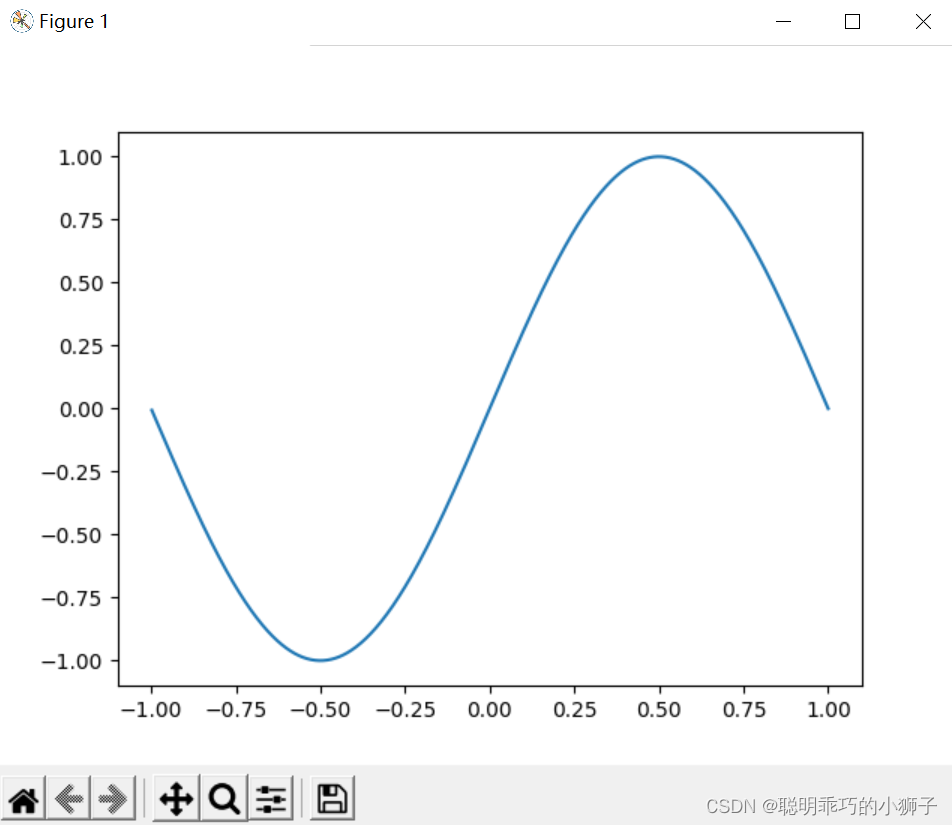
4.非等分点（切比雪夫高斯巴托点）、多项式插值法
将

for i in range(N):
    x.append(round((-1+(2/N)*(N-i)),3))

改为

for i in range(N):
    x.append(math.cos(i*pi/N))

即可
结果：

耗时： 0.09850764274597168
误差： 1.5787371410169726e-13