1 引言
马尔可夫性:无后效性,指系统的下个状态只与当前状态信息有关,而与更早之前的状态无关;
马尔可夫链(Markov Chain, MC):系统的下一个状态只与当前状态相关;
马尔可夫决策过程(Markov Decision Process, MDP):具有马尔可夫性,与MC不同的是MDP还考虑了动作,即系统下个状态不仅和当前的状态有关,也和当前采取的动作有关。
以下棋为例:我们在某个局面(状态
s
i
s_i
si?)走了一步(动作
a
i
a_i
ai?),这时对手的选择(导致下个状态
s
i
+
1
s_{i+1}
si+1?)我们是不能确定的,但是他的选择只和
s
i
s_i
si?和
a
i
a_i
ai?有关,而不用考虑更早之前的状态和动作。
2 马尔可夫决策过程
一个马尔可夫决策过程可以由一个四元组表示:
M
=
(
S
,
A
,
P
s
a
,
R
)
(1)
M = (S, A, P_{sa}, R) \tag1
M=(S,A,Psa?,R)(1)
- S = { s 1 , s 2 , … , s k } S = \{s_1, s_2, \dots, s_k\} S={s1?,s2?,…,sk?}:状态集(states), s i s_i si?表示第 i i i步的状态;
- A = { a 1 , a 2 , … , a k } A = \{a_1, a_2, \dots, a_k\} A={a1?,a2?,…,ak?}:一组动作(actions), a i a_i ai?表示第 i i i步的动作;
- P s a P_{sa} Psa?:状态转移概率,当前 s i ∈ S s_i \in S si?∈S状态下,经过 a i ∈ A a_i \in A ai?∈A作用后,会转移到的其它状态的概率分布情况,例如比如,在状态 s i ∈ S s_i \in S si?∈S下执行动作 a i ∈ A a_i \in A ai?∈A,转移到 s i + 1 ∈ S s_{i+1} \in S si+1?∈S的概率可以表示为 p ( s i + 1 ∣ s i , a i ) p(s_{i+1} \vert s_i, a_i) p(si+1?∣si?,ai?);
- R : S × A ? R R: S \times A \mapsto \mathbb{R} R:S×A?R:回报函数(reward function),如果回报只与状态有关,可以简化为 R : S ? R R: S \mapsto \mathbb{R} R:S?R。如果一组 ( s i , a i ) (s_{i},a_i) (si?,ai?)转移到了下个状态 s i + 1 s_{i+1} si+1?,那么回报函数可记为 r ( s i + 1 ∣ s i , a i ) r(s_{i+1}|s_i, a_i) r(si+1?∣si?,ai?)。如果 ( s i , a i ) (s_i,a_i) (si?,ai?)对应的下个状态 s i + 1 s_{i+1} si+1?是唯一的,那么回报函数也可以记为 r ( s i , a i ) r(s_i,a_i) r(si?,ai?)。
MDP 的动态过程如下:
- 智能体(agent)的初始状态为 s 0 s_0 s0?;
- 从 A A A 中挑选一个动作 a 0 a_0 a0?执行,执行后,agent 按 P s a P_{sa} Psa?概率随机转移到了下一个 s 1 s_1 s1?状态, s 1 ∈ P s 0 a 0 s_1 \in P_{s_0a_0} s1?∈Ps0?a0??。
- 然后再执行一个动作 a 1 a_1 a1?,就转移到了 s 2 s_2 s2?,接下来再执行 a 2 a_2 a2?,…;
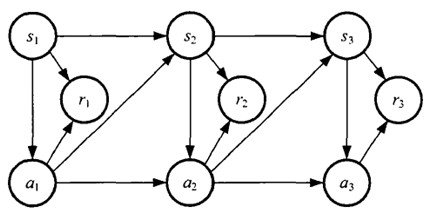
- 可以用下面的图表示状态转移的过程:

如果回报
r
i
r_i
ri?是根据状态
s
i
s_i
si?和动作
a
i
a_i
ai?得到的,则MDP可以如图表示:
3 值函数(value function)
增强学习学到的是一个从环境状态到动作的映射(即行为策略),记为策略 π : S → A π: S→A π:S→A。而增强学习往往又具有延迟回报的特点: 如果在第 n n n步输掉了棋,那么只有状态 s n s_n sn?和动作 a n a_n an?获得了立即回报 r ( s n , a n ) = ? 1 r(s_n,a_n)=-1 r(sn?,an?)=?1,前面的所有状态立即回报均为0。所以对于之前的任意状态 s s s和动作 a a a,立即回报函数 r ( s , a ) r(s,a) r(s,a)无法说明策略的好坏。因而需要定义值函数(value function,又叫效用函数)来表明当前状态下策略 π π π的长期影响。
- V π ( s ) V^π(s) Vπ(s):策略 π π π下,状态 s s s的值函数;
- r i r_i ri?:未来第 i i i步的立即回报。
常见的值函数有以下三种:
V
π
(
s
)
=
E
π
[
∑
i
=
0
h
r
i
∣
s
0
=
s
]
(2)
V^π(s) = E_{\pi}\left[\sum_{i=0}^{h} r_i \vert s_0 = s \right] \tag2
Vπ(s)=Eπ?[i=0∑h?ri?∣s0?=s](2)
V π ( s ) = lim ? h → ∞ E π [ 1 h ∑ i = 0 h r i ∣ s 0 = s ] (3) V^π(s) = \lim_{h \rightarrow \infty}E_{\pi}\left[\frac{1}{h}\sum_{i=0}^{h} r_i \vert s_0 = s \right] \tag3 Vπ(s)=h→∞lim?Eπ?[h1?i=0∑h?ri?∣s0?=s](3)
V
π
(
s
)
=
E
π
[
∑
i
=
0
∞
γ
i
r
i
∣
s
0
=
s
]
(4)
V^π(s) = E_{\pi}\left[\sum_{i=0}^{\infty} \gamma^{i} r_i \vert s_0 = s \right] \tag4
Vπ(s)=Eπ?[i=0∑∞?γiri?∣s0?=s](4)
其中:
a) 是采用策略π的情况下未来有限h步的期望立即回报总和;
b) 是采用策略π的情况下期望的平均回报;
c) 是值函数最常见的形式,式中
γ
∈
[
0
,
1
]
γ∈[0,1]
γ∈[0,1]称为折合因子,表明了未来的回报相对于当前回报的重要程度。特别的,
γ
=
0
γ=0
γ=0时,相当于只考虑立即不考虑长期回报,
γ
=
1
γ=1
γ=1时,将长期回报和立即回报看得同等重要。
4 对2048游戏的建模
s
1
s_1
s1?: 初始化状态,随机产生的棋盘;
a
1
a_1
a1?:用户连接相同的数字后,系统为棋盘分配新数字的动作;
s
2
s_2
s2?:用户选择如何连线后导致的下一个棋盘,该棋盘依然有空缺,需要填充新数字;
p
(
s
2
∣
s
1
,
a
1
)
p(s_{2} \vert s_1, a_1)
p(s2?∣s1?,a1?):经过
a
1
a_1
a1?操作后状态从
s
1
s_1
s1?到
s
2
s_2
s2?的概率,这个我觉得可以通过统计得到;
奖励函数:是设计的难点
如何进行训练:也是一个难点