[人工智能]OvO多分类策略简述

OvO
先来看看下面的训练数据集，现在需要对其进行分类问题，你会使用什么算法来解决呢？逻辑回归吗？可是别忘了逻辑回归是用于解决二分类问题的，但是现在这里有三类，我们有什么方法来解决呢？

是否想到以两两之间进行分类呢？即一对一的来进行，所谓的“一”，指的是类别。而“对”指的是从训练集中划分不同的两个类别的组合来训练出多个分类器。简单来说就是用二分类算法来解决多分类问题的一种策略，原理思想也可以说还是二分类的问题。划分的规则很简单，就是组合(Cn2 ，其中n表示训练集中类别的数量，在这个例子中为3，如下图两两进行组合)

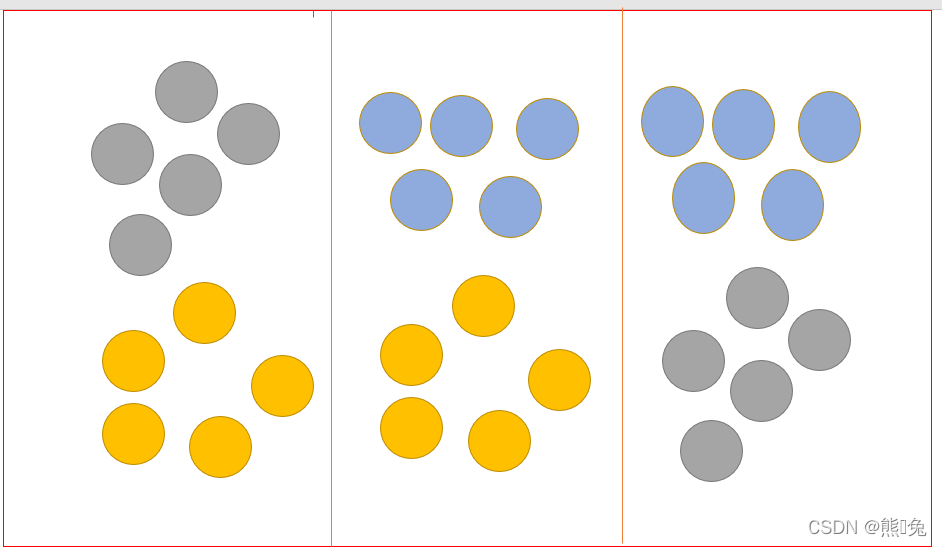
在预测阶段，只需要将测试样本分别扔给训练阶段训练好的3个分类器进行预测，最后将3个分类器（上面三个组合训练的分类器）预测出的结果进行投票统计，票数最高的结果为预测结果。
代码实现：

import numpy as np
# 逻辑回归
class tiny_logistic_regression(object):
    def __init__(self):
        # 权重项和偏置项
        self.coef_ = None
        self.intercept_ = None
        #所有的W和b
        self._theta = None
        #0,1到标签的映射
        self.label_map = {}
        
    # 构造sigmod函数
    def _sigmoid(self, x):
        return 1. / (1. + np.exp(-x))
        
    #训练数据，构造损失函数
    def fit(self, train_datas, train_labels, learning_rate=1e-4, n_iters=1e3):
        #loss损失函数
        def J(theta, X_b, y):
            y_hat = self._sigmoid(X_b.dot(theta))
            try:
                return -np.sum(y*np.log(y_hat)+(1-y)*np.log(1-y_hat)) / len(y)
            except:
                return float('inf')
        # 算theta对loss的偏导
        def dJ(theta, X_b, y):
            return X_b.T.dot(self._sigmoid(X_b.dot(theta)) - y) / len(y)
        # 批量梯度下降
        def gradient_descent(X_b, y, initial_theta, leraning_rate, n_iters=1e2, epsilon=1e-6):
            theta = initial_theta
            cur_iter = 0
            while cur_iter < n_iters:
                gradient = dJ(theta, X_b, y)
                last_theta = theta
                # 进行梯度下降，更新参数
                theta = theta - leraning_rate * gradient
                if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
                    break
                cur_iter += 1
            return theta
            
        unique_labels = list(set(train_labels))
        labels = train_labels.copy()
        self.label_map[0] = unique_labels[0]
        labels[train_labels == unique_labels[0]] = 0
        self.label_map[1] = unique_labels[1]
        labels[train_labels == unique_labels[1]] = 1
        X_b = np.hstack([np.ones((len(train_datas), 1)), train_datas])
        initial_theta = np.zeros(X_b.shape[1])
        self._theta = gradient_descent(X_b, labels, initial_theta, learning_rate, n_iters)
        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]
        return self
    #预测概率分布
    def predict_proba(self, X):
        X_b = np.hstack([np.ones((len(X), 1)), X])
        return self._sigmoid(X_b.dot(self._theta))
    #预测
    def predict(self, X):
        proba = self.predict_proba(X)
        result = np.array(proba >= 0.5, dtype='int')
        for i in range(len(result)):
            if result[i] == 0:
                result[i] = self.label_map[0]
            else:
                result[i] = self.label_map[1]
        return result
class OvO(object):
    def __init__(self):
        # 用于保存训练时各种模型的list
        self.models = []
    def fit(self, train_datas, train_labels):
        '''
        OvO的训练阶段，将模型保存到self.models中
        :param train_datas: 训练集数据，类型为ndarray
        :param train_labels: 训练集标签，类型为ndarray，shape为(-1,)
        :return:None
        '''
        unique_labels = list(set(train_labels))
        for i in range(len(unique_labels)):
            for j in range(i+1, len(unique_labels)):
                datas = train_datas[(train_labels == unique_labels[i]) | (train_labels == unique_labels[j])]
                labels = train_labels[(train_labels == unique_labels[i]) | (train_labels == unique_labels[j])]
                # tiny_logistic_regression()二分类分类器
                lr = tiny_logistic_regression()
                lr.fit(datas, labels)
                self.models.append(lr)
                
    def predict(self, test_datas):
        '''
        OvO的预测阶段
        :param test_datas:测试集数据，类型为ndarray
        :return:预测结果，类型为ndarray
        '''

        def _predict(models, test_data):
            # 变形
            test_data = np.reshape(test_data, (1, -1))
            vote = {}
            # 计票
            for model in models:
                pred = model.predict(test_data)[0]
                if pred not in vote:
                    vote[pred] = 1
                else:
                    vote[pred] += 1
            vote = sorted(vote.items(), key=lambda x: x[1], reverse=True)
            return vote[0][0]
            
        predict = []
        for data in test_datas:
            predict.append(_predict(self.models, data))
        return np.array(predict)

OvR
如果想要使用逻辑回归算法来解决这种3分类问题，可以使用OvR。OvR(One Vs Rest)是使用二分类算法来解决多分类问题的一种策略。从字面意思可以看出它的核心思想就是一对剩余。一对剩余的意思是当要对n种类别的样本进行分类时，分别取一种样本作为一类，将剩余的所有类型的样本看做另一类，这样就形成了n个二分类问题。所以和OvO一样，在训练阶段需要进行划分。如下图所示。

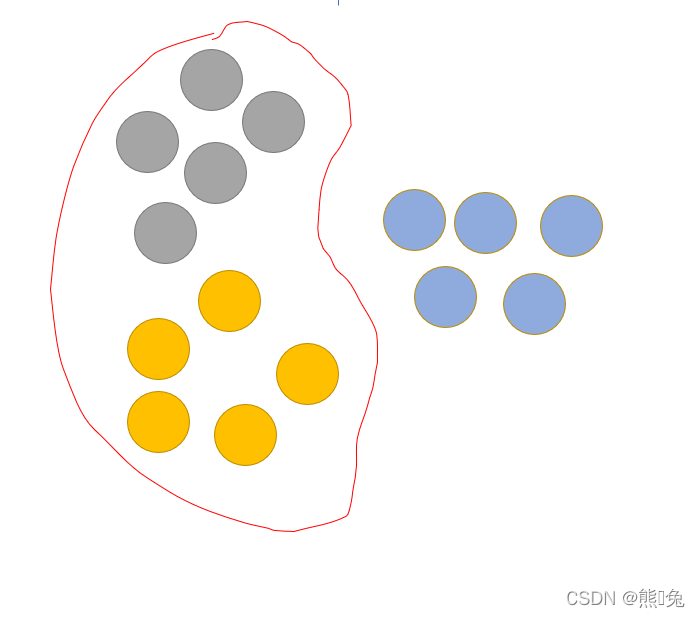
分别用这3种划分，划分出来的训练集训练二分类分类器，就能得到3个分类器。此时训练阶段已经完毕。