[人工智能]徐亦达 概率模型学习

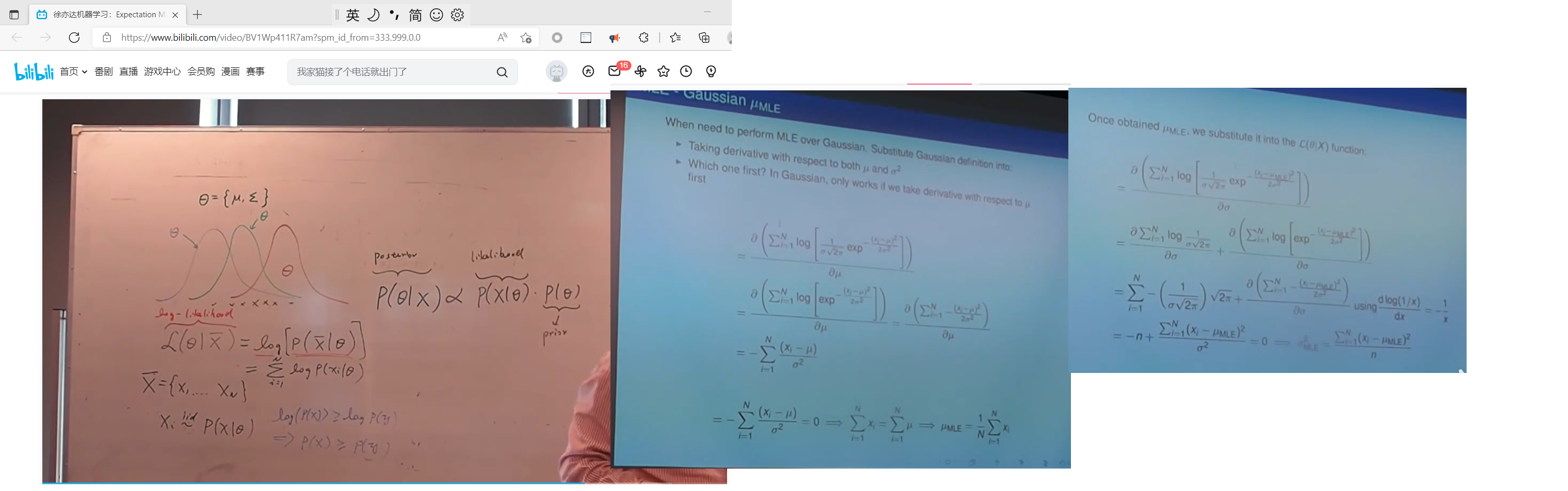
单高斯分布 MLE

posterior 正比例于 likelihood * prior
$p(\theta |x)\propto p(x|\theta )?p(\theta )$
$参数\theta 的后验分布\propto 参数\theta 表示的x分布上已知样本有多大概率?参数\theta 的先验分布$
$参数的后验\propto 样本的likelihood?参数的先验$
MLE : max log_likelihood estimator
MAP: max a posterior

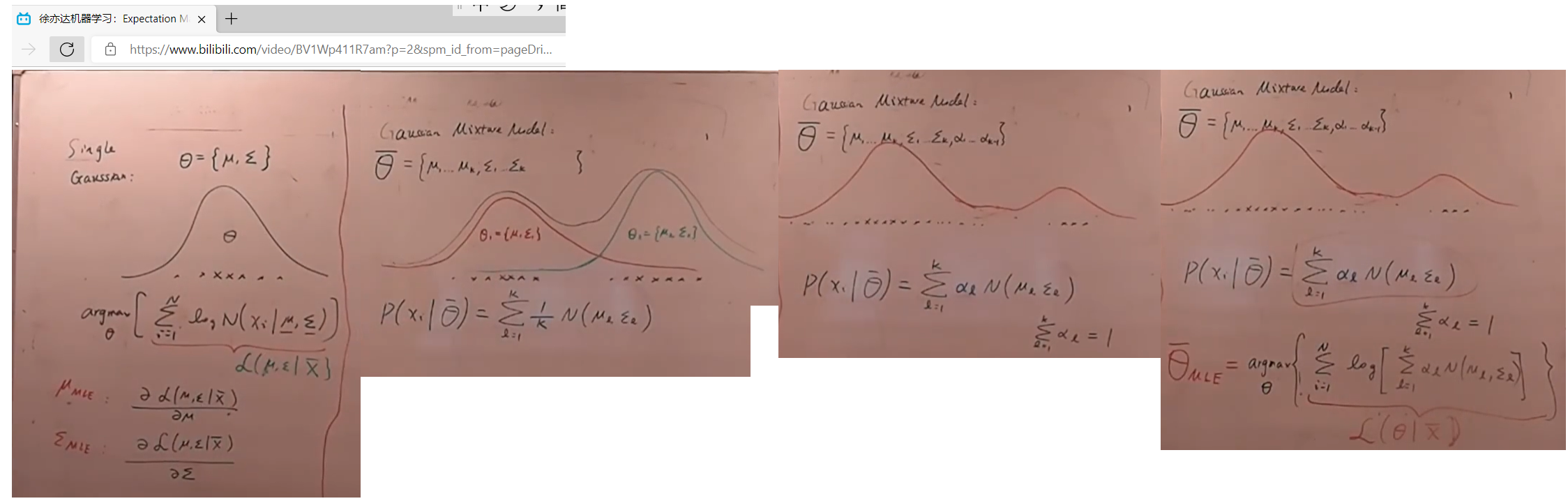
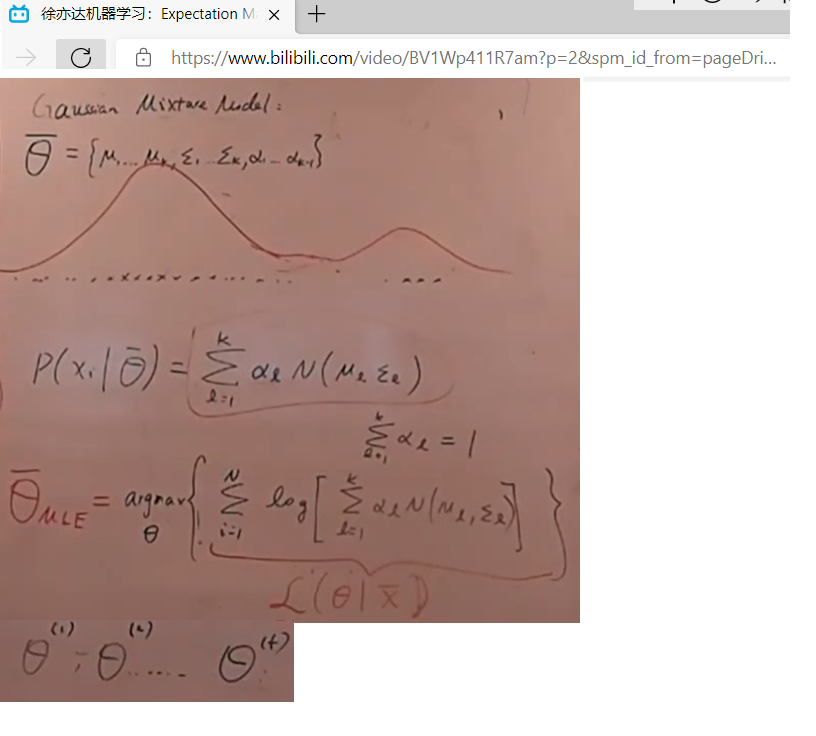
混合高斯分布（多个高斯分布混合在一起） MLE

单高斯混合分布, 只需要令: $\frac{?L}{?u}=0$， $\frac{?L}{?\Sigma }=0$ ； 即可一步到位的精确的求出 $u和\Sigma$的值

混合高斯分布，由于L中有log(多个式子求和)， 而log(多个式子求和)求出导数是可以的， 但 要解 $\frac{?L}{?u}=0$、 $\frac{?L}{?\Sigma }=0$ 比较难， 所以 没法一步到位精确求解，只能迭代求解 。 此迭代求解方法 即 EM算法

即:
解方程 $\frac{?log(多个式子的乘积)}{?其中一个变量}$ = 0 较难
解方程 $\frac{?log(多个式子的和)}{?其中一个变量}$ = 0 较容易
注意：两者的导数都可以求得出来

EM算法（混合高斯分布）

中心点或均值u、形状或协方差矩阵 $\Sigma$

em算法迭代过程演示

$em算法参数\Theta 初始化为{\Theta }^{(1)}$
$em算法第1次迭代结果{\Theta }^{(2)}$
$em算法第2次迭代结果{\Theta }^{(3)}$
$em算法第f次迭代结果(em算法收敛时的结果){\Theta }^{(f)}$

em迭代描述

em算法迭代过程描述:
${\Theta }^{(g+1)}={\Theta }^{(g)}$
${\Theta }^{(g+1)}={argmax}_{\Theta }{\int }_{z}logp(X,z|\Theta )p(z|X,{\Theta }^{(g)})dz$ (这里看完后 弄清楚了 回头要明确一下)

em算法引入的隐变量z应该保持边缘分布不变:

这里的$z_i$ 就是前面"EM算法（混合高斯分布）" 中的${\alpha }_l$
上图$p(x_i)$ 就是 $p(x_i|\Theta )$

em算法中 log_likelihood $logp(X|\Theta )$ 逐步增加 推导 1

如果 对于任意 $\Theta$ 有 $H({\Theta }^{(g)},{\Theta }^{(g)})\ge H(\Theta ,{\Theta }^{(g)})$，
则 $H({\Theta }^{(g)},{\Theta }^{(g)})\ge H({\Theta }^{(g+1)},{\Theta }^{(g)})$

em算法中 log_likelihood $logp(X|\Theta )$ 逐步增加 推导 2

Jensen’s inequality (琴生不等式)

…

sklearn 手写数字数据集 gmm 例子 (图片的一个像素点被当成一个随机变量)

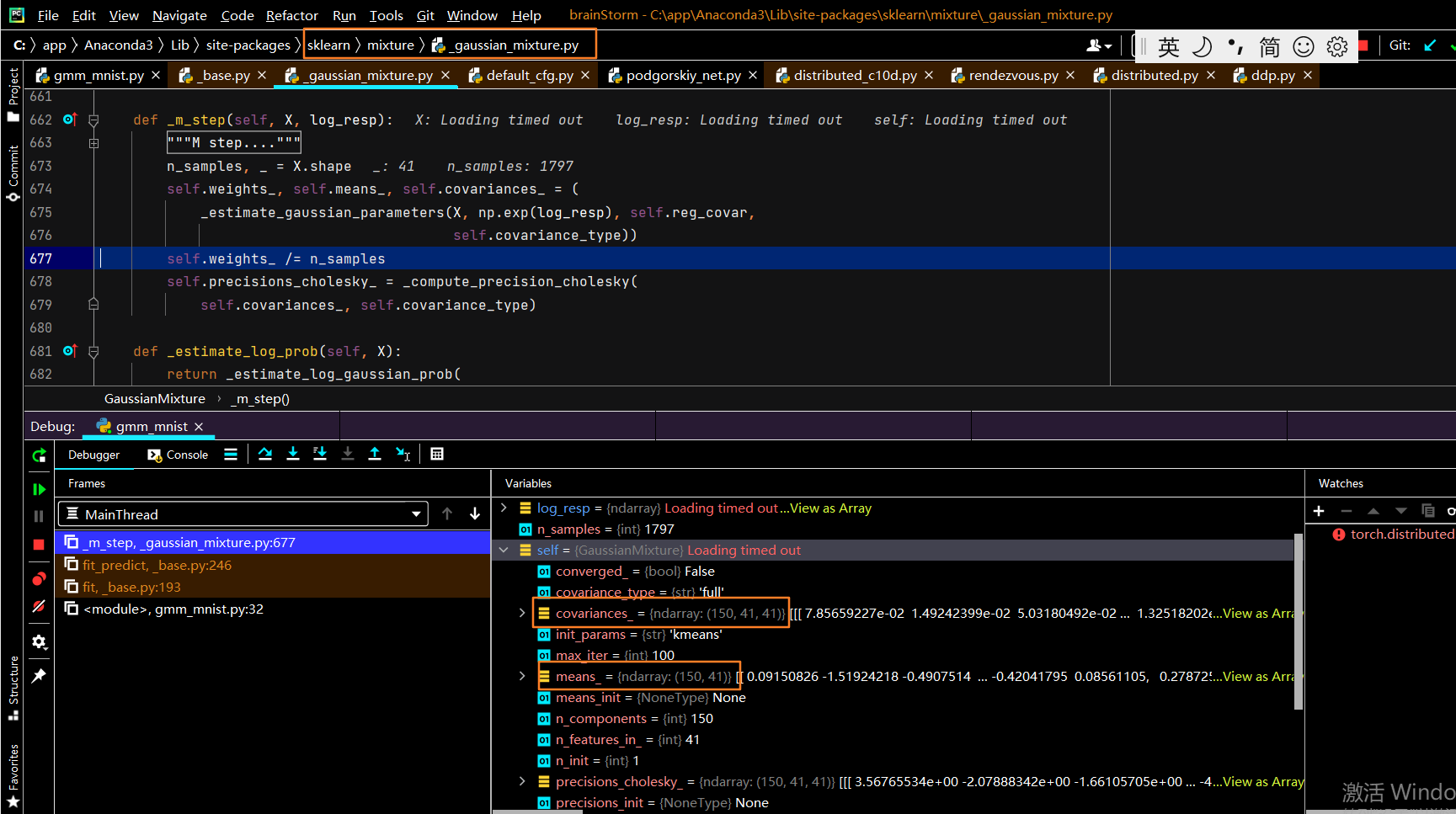
"""sklearn 手写数字数据集 gmm 例子 (图片的一个像素点被当成一个随机变量)
来自 https://jakevdp.github.io/PythonDataScienceHandbook/05.12-gaussian-mixtures.html
或 https://github.com/jakevdp/PythonDataScienceHandbook/blob/master/notebooks/05.12-Gaussian-Mixtures.ipynb
"""

import numpy as np
from sklearn.datasets import load_digits
from matplotlib import pyplot as plt
def plot_digits(data):
    fig, ax = plt.subplots(10, 10, figsize=(8, 8),
                           subplot_kw=dict(xticks=[], yticks=[]))
    fig.subplots_adjust(hspace=0.05, wspace=0.05)
    for i, axi in enumerate(ax.flat):
        im = axi.imshow(data[i].reshape(8, 8), cmap='binary')
        im.set_clim(0, 16)
    plt.show()

digits = load_digits()
print(digits.data.shape)#(1797, 64)

# plot_digits(digits.data)

from sklearn.decomposition import PCA
pca = PCA(n_components=0.99, whiten=True)
data = pca.fit_transform(digits.data)
print(data.shape)#(1797, 41)

from sklearn.mixture import GaussianMixture
"""
n_components = np.arange(50, 210, 10)
models = [GaussianMixture(n_components=n, covariance_type='full', random_state=0) for n in n_components]
aics = [model.fit(data).aic(data) for model in models]
plt.plot(n_components, aics); plt.show()
"""

gmm = GaussianMixture(n_components=150, covariance_type='full', random_state=0)
gmm.fit(data)
print(gmm.converged_)

data_new,label_new = gmm.sample(n_samples=100)
print(data_new.shape)

digits_new = pca.inverse_transform(data_new)
plot_digits(digits_new)