文章目录
1.高斯过程简介
1.1定义
高斯过程是随机变量的集合,其中任意有限个随机变量具有联合高斯分布。
在函数空间(function-space view)的观点中,高斯过程可以看作是一个定义在函数上的分布,并且直接在函数空间中进行inference。
与之等价的观点是权空间观点(weight-space view),在权空间中进行推断,对权向量的不同抽样将产生不同的函数,这与函数空间观点是一致的,但是函数空间的观点更为直接和抽象。
注 :为方便起见,本文不刻意区分概率密度和概率质量函数,向量用小写字母如 x x x表示,矩阵用大写字母如 X X X表示,标量将作特别说明。
2.部分基础知识(已具备的直接跳至第3节)
2.1 部分矩阵计算基础
2.1.1 分块矩阵求逆
感兴趣可看推导过程,否则直接看最后结论。
设矩阵
(
A
B
C
D
)
\begin{pmatrix} A&B\\ C&D \end{pmatrix}
(AC?BD?)
为可逆矩阵,下面求该矩阵的逆(推导是逆矩阵存在的假设下进行)。
设
(
A
B
C
D
)
(
X
Y
)
=
(
P
Q
)
\begin{pmatrix} A&B\\ C&D \end{pmatrix} \begin{pmatrix} X\\ Y \end{pmatrix}=\begin{pmatrix} P\\ Q \end{pmatrix}
(AC?BD?)(XY?)=(PQ?),
可得
{
A
X
+
B
Y
=
P
…
…
(
1
)
C
X
+
D
Y
=
Q
…
…
(
2
)
\begin{cases} AX+BY=P\dots\dots(1)\\ CX+DY=Q\dots\dots(2) \end{cases}
{AX+BY=P……(1)CX+DY=Q……(2)?
由
(
2
)
(2)
(2)可得,
Y
=
D
?
1
(
Q
?
C
X
)
…
…
(
3
)
Y=D^{-1}(Q-CX)\dots\dots(3)
Y=D?1(Q?CX)……(3)
将
(
3
)
(3)
(3)带入(1)并移项整理可得,
X
=
(
A
?
B
D
?
1
C
)
?
1
(
P
?
B
D
?
1
Q
)
…
…
(
4
)
X=(A-BD^{-1}C)^{-1}(P-BD^{-1}Q)\dots\dots(4)
X=(A?BD?1C)?1(P?BD?1Q)……(4)
将
(
4
)
(4)
(4)带入
(
3
)
(3)
(3)整理可得,
Y
=
D
?
1
(
Q
?
C
(
A
?
B
D
?
1
C
)
?
1
(
P
?
B
D
?
1
Q
)
)
Y=D^{-1}(Q-C(A-BD^{-1}C)^{-1}(P-BD^{-1}Q))
Y=D?1(Q?C(A?BD?1C)?1(P?BD?1Q))
令
M
=
(
A
?
B
D
?
1
C
)
?
1
M=(A-BD^{-1}C)^{-1}
M=(A?BD?1C)?1,其实
M
M
M就是关于
D
D
D的舒尔补(The Shur complements)。
分别令
{
P
=
I
Q
=
0
及
{
P
=
0
Q
=
I
\begin{cases} P=I\\ Q=\mathbf{}{0} \end{cases}及 \begin{cases} P=\mathbf{}{0}\\ Q=I \end{cases}
{P=IQ=0?及{P=0Q=I?
其中
I
I
I为单位矩阵。
可得原分块矩阵的逆矩阵
(
M
?
M
B
D
?
1
?
D
?
1
C
M
D
?
1
+
D
?
1
C
M
B
D
?
1
)
…
…
(
5
)
\begin{pmatrix} M&-MBD^{-1}\\ -D^{-1}CM&D^{-1}+D^{-1}CMBD^{-1} \end{pmatrix}\dots\dots(5)
(M?D?1CM??MBD?1D?1+D?1CMBD?1?)……(5)
2.1.2 矩阵求逆引理
(
A
+
B
C
D
)
?
1
=
A
?
1
?
A
?
1
B
(
I
+
C
D
A
?
1
B
)
?
1
C
D
A
?
1
…
…
(
6
)
(A+BCD)^{-1}=A^{-1}-A^{-1}B(I+CDA^{-1}B)^{-1}CDA^{-1}\dots\dots(6)
(A+BCD)?1=A?1?A?1B(I+CDA?1B)?1CDA?1……(6)
其中矩阵
A
A
A可逆。
证明:
设
(
A
+
B
C
D
)
X
=
I
设(A+BCD)X=I
设(A+BCD)X=I,其中
I
I
I为单位矩阵,则可得
{
A
X
+
B
Y
=
I
…
…
(
7
)
Y
=
B
C
X
…
…
(
8
)
\begin{cases} AX+BY=I\dots\dots(7)\\ Y=BCX\dots\dots(8) \end{cases}
{AX+BY=I……(7)Y=BCX……(8)?
由
(
7
)
(7)
(7)可得
X
=
A
?
1
(
b
?
B
Y
)
X=A^{-1}(b-BY)
X=A?1(b?BY),并带入
(
8
)
(8)
(8)整理得
Y
=
(
I
+
C
D
A
?
1
B
)
?
1
C
D
A
?
1
Y=(I+CDA^{-1}B)^{-1}CDA^{-1}
Y=(I+CDA?1B)?1CDA?1
回代得到
X
=
A
?
1
?
A
?
1
B
(
I
+
C
D
A
?
1
B
)
?
1
C
D
A
?
1
X=A^{-1}-A^{-1}B(I+CDA^{-1}B)^{-1}CDA^{-1}
X=A?1?A?1B(I+CDA?1B)?1CDA?1
2.2 多元高斯分布
2.2.1 联合分布
设
x
x
x是一个
n
n
n维向量,则其概率密度函数是
p
(
x
)
=
1
(
2
π
)
n
2
∣
Σ
∣
1
2
e
x
p
{
?
1
2
(
x
?
μ
)
T
Σ
?
1
(
x
?
μ
)
}
…
…
(
9
)
p(x) = \frac{1} {(2\pi)^\frac{n}{2} \begin{vmatrix} \Sigma \end{vmatrix} ^\frac{1}{2} } exp{\{ -\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu) \}}\dots\dots(9)
p(x)=(2π)2n?∣∣?Σ?∣∣?21?1?exp{?21?(x?μ)TΣ?1(x?μ)}……(9)
其中, Σ \Sigma Σ和 μ \mu μ分别是随机向量 x x x的协方差矩阵和均值向量。
多维高斯分布具有非常良好的性质:
- 边缘分布满足高斯分布。
- 条件分布满足高斯分布。
- 各分量的线性组合也是高斯随机变量。
2.2.2 条件概率分布
设随机向量
x
x
x符合多维高斯分布,将其分为不相交的两部分
x
=
(
x
a
x
b
)
x=\begin{pmatrix} x_a\\x_b \end{pmatrix}
x=(xa?xb??),
x
x
x的均值向量
μ
=
(
μ
a
μ
b
)
\mu=\begin{pmatrix} \mu_a\\\mu_b \end{pmatrix}
μ=(μa?μb??)
协方差矩阵为
Σ
=
(
Σ
a
a
Σ
a
b
Σ
b
a
Σ
b
b
)
\Sigma=\begin{pmatrix} \Sigma_{aa}&\Sigma_{ab}\\ \Sigma_{ba}&\Sigma_{bb} \end{pmatrix}
Σ=(Σaa?Σba??Σab?Σbb??)
精度矩阵为
Λ
=
Σ
?
1
=
(
Λ
a
a
Λ
a
b
Λ
b
a
Λ
b
b
)
\Lambda=\Sigma^{-1}=\begin{pmatrix} \Lambda_{aa}&\Lambda_{ab}\\ \Lambda_{ba}&\Lambda_{bb} \end{pmatrix}
Λ=Σ?1=(Λaa?Λba??Λab?Λbb??)
其中协方差矩阵是正定的,因为其对称性,
Σ
a
b
=
Σ
a
b
T
\Sigma_{ab}=\Sigma_{ab}^T
Σab?=ΣabT?,
Λ
a
b
=
Λ
a
b
T
\Lambda_{ab}=\Lambda_{ab}^T
Λab?=ΛabT?。
注意这是分块矩阵,不能对每个矩阵块简单求逆,我们使用公式
(
5
)
(5)
(5),可得
Λ
a
a
=
(
Σ
a
a
?
Σ
a
b
Σ
b
b
?
1
Σ
b
a
)
?
1
…
…
(
10
)
\Lambda_{aa}=(\Sigma_{aa}-\Sigma_{ab}\Sigma_{bb}^{-1}\Sigma_{ba})^{-1}\dots\dots(10)
Λaa?=(Σaa??Σab?Σbb?1?Σba?)?1……(10)
Λ a b = ? ( Σ a a ? Σ a b Σ b b ? 1 Σ b a ) ? 1 Σ a b Σ b b ? 1 … … ( 11 ) \Lambda_{ab}=-(\Sigma_{aa}-\Sigma_{ab}\Sigma_{bb}^{-1}\Sigma_{ba})^{-1}\Sigma_{ab}\Sigma_{bb}^{-1}\dots\dots(11) Λab?=?(Σaa??Σab?Σbb?1?Σba?)?1Σab?Σbb?1?……(11)
接下来,我们求在给定 x b x_b xb?的条件下, x a x_a xa?的条件概率分布。注意到高斯分布的形式主要取决于指数项,因此我们使用配方法来找出相应的均值和协方差矩阵,而不需要考虑归一化系数,就可以得到条件分布的形式。
指数项为
?
1
2
(
x
a
?
μ
a
)
T
Λ
a
a
(
x
a
?
μ
a
)
?
1
2
(
x
a
?
μ
a
)
T
Λ
a
b
(
x
b
?
μ
b
)
?
1
2
(
x
b
?
μ
a
)
T
Λ
b
a
(
x
a
?
μ
a
)
?
1
2
(
x
b
?
μ
b
)
T
Λ
b
b
(
x
b
?
μ
b
)
…
(
12
)
-\frac{1}{2}(x_a-\mu_a)^T\Lambda_{aa}(x_a-\mu_a) -\frac{1}{2}(x_a-\mu_a)^T\Lambda_{ab}(x_b-\mu_b) -\frac{1}{2}(x_b-\mu_a)^T\Lambda_{ba}(x_a-\mu_a) -\frac{1}{2}(x_b-\mu_b)^T\Lambda_{bb}(x_b-\mu_b)\dots(12)
?21?(xa??μa?)TΛaa?(xa??μa?)?21?(xa??μa?)TΛab?(xb??μb?)?21?(xb??μa?)TΛba?(xa??μa?)?21?(xb??μb?)TΛbb?(xb??μb?)…(12)
观察式(9)中指数项的形式,可发现精度矩阵出现在
x
x
x的二次项中,精度矩阵和均值的乘积出现在
x
T
x^T
xT的线性项中,因此我们可得
Σ
a
∣
b
=
Λ
a
a
?
1
…
…
(
13
)
Λ
a
b
μ
a
∣
b
=
Λ
a
a
μ
a
?
Λ
a
b
(
x
b
?
μ
b
)
…
…
(
1
3
′
)
\Sigma_{a|b}=\Lambda_{aa}^{-1}\dots\dots(13)\\ \Lambda_{ab}\mu_{a|b}=\Lambda_{aa}\mu_a-\Lambda_{ab}(x_b-\mu_b)\dots\dots(13')
Σa∣b?=Λaa?1?……(13)Λab?μa∣b?=Λaa?μa??Λab?(xb??μb?)……(13′)
由式(10)(11)可得
μ
a
∣
b
=
(
μ
a
?
Λ
a
a
?
1
Λ
a
b
(
x
b
?
μ
b
)
)
…
…
(
14
)
\mu_{a|b}=(\mu_a-\Lambda_{aa}^{-1}\Lambda_{ab}(x_b-\mu_b))\dots\dots(14)
μa∣b?=(μa??Λaa?1?Λab?(xb??μb?))……(14)
这样我们就得到了
p
(
x
a
∣
x
b
)
p(x_a|x_b)
p(xa?∣xb?)的分布,我们发现它的协方差是不依赖与
x
b
x_b
xb?的,而均值是
x
b
x_b
xb?的线性函数,这实际上是线性高斯模型的一个例子。
2.2.3 简单的线性高斯模型及贝叶斯定理
贝叶斯公式:
p
(
x
∣
y
)
=
p
(
x
)
p
(
y
∣
x
)
p
(
y
)
…
…
(
15
)
p(x|y)=\frac{p(x)p(y|x)}{p(y)}\dots\dots(15)
p(x∣y)=p(y)p(x)p(y∣x)?……(15)
我们设
x
~
G
a
u
s
s
i
a
n
(
x
∣
μ
,
Λ
?
1
)
y
∣
x
~
G
a
u
s
s
i
a
n
(
y
∣
A
x
+
b
,
L
?
1
)
x\sim Gaussian(x|\mu, \Lambda^{-1})\\ y|x\sim Gaussian(y|Ax+b, L^{-1})
x~Gaussian(x∣μ,Λ?1)y∣x~Gaussian(y∣Ax+b,L?1)
其中
Λ
和
L
\Lambda和L
Λ和L为
x
和
y
x和y
x和y的精度矩阵,
y
y
y的均值为
x
x
x的线性函数。
接下来,我们想要知道
z
=
(
x
y
)
z=\begin{pmatrix} x\\ y \end{pmatrix}
z=(xy?)的联合分布。
依然使用配方的方法,关注于指数项的系数。根据式(15)可得,
l
n
p
(
z
)
∝
l
n
p
(
x
)
+
l
n
p
(
y
∣
x
)
lnp(z)\propto lnp(x)+lnp(y|x)
lnp(z)∝lnp(x)+lnp(y∣x)
因此观察
?
1
2
(
x
?
μ
)
T
Λ
(
x
?
μ
)
?
1
2
(
y
?
A
x
?
b
)
T
L
(
y
?
A
x
?
b
)
-\frac{1}{2}(x-\mu)^T\Lambda(x-\mu) -\frac{1}{2}(y-Ax-b)^TL(y-Ax-b)
?21?(x?μ)TΛ(x?μ)?21?(y?Ax?b)TL(y?Ax?b)
整理二次项,有
?
1
2
x
T
(
Λ
+
A
T
L
A
)
x
?
1
2
y
T
L
y
+
1
2
y
T
L
A
x
+
1
2
x
T
A
T
L
y
=
?
1
2
(
x
T
y
T
)
(
Λ
+
A
T
L
A
A
T
L
L
A
L
)
(
x
y
)
-\frac{1}{2}x^T(\Lambda+A^TLA)x -\frac{1}{2}y^TLy +\frac{1}{2}y^TLAx +\frac{1}{2}x^TA^TLy\\ =-\frac{1}{2}\begin{pmatrix}x^T&y^T\end{pmatrix} \begin{pmatrix} \Lambda+A^TLA&A^TL\\ LA&L \end{pmatrix} \begin{pmatrix} x\\ y \end{pmatrix}
?21?xT(Λ+ATLA)x?21?yTLy+21?yTLAx+21?xTATLy=?21?(xT?yT?)(Λ+ATLALA?ATLL?)(xy?)
因此可得精度矩阵
R
[
z
]
=
(
Λ
+
A
T
L
A
A
T
L
L
A
L
)
…
(
16
)
R[z]=\begin{pmatrix} \Lambda+A^TLA&A^TL\\ LA&L \end{pmatrix}\dots(16)
R[z]=(Λ+ATLALA?ATLL?)…(16)
根据公式(5)可得协方差矩阵,
C
o
v
[
z
]
=
(
Λ
?
1
Λ
?
1
A
T
A
Λ
?
1
L
?
1
+
A
Λ
?
1
A
T
)
…
(
17
)
Cov[z]=\begin{pmatrix} \Lambda^{-1}&\Lambda^{-1}A^T\\ A\Lambda^{-1}&L^{-1}+A\Lambda^{-1}A^T \end{pmatrix}\dots(17)
Cov[z]=(Λ?1AΛ?1?Λ?1ATL?1+AΛ?1AT?)…(17)
再观察一次项
x
T
Λ
μ
?
x
T
A
T
L
b
+
y
T
L
b
=
(
x
y
)
T
(
Λ
μ
?
A
T
L
b
L
b
)
x^T\Lambda\mu-x^TA^TLb+y^TLb=\begin{pmatrix}x\\y\end{pmatrix}^T \begin{pmatrix} \Lambda\mu-A^TLb\\ Lb \end{pmatrix}
xTΛμ?xTATLb+yTLb=(xy?)T(Λμ?ATLbLb?)
由此并根据式(13’)(16)可得均值
E
[
z
]
=
(
μ
A
μ
+
b
)
…
…
(
18
)
E[z]=\begin{pmatrix}\mu\\A\mu+b\end{pmatrix}\dots\dots(18)
E[z]=(μAμ+b?)……(18)
这个结果也是符合我们的直觉的,由此可得
y
y
y的边缘分布为
E
[
y
]
=
A
μ
+
b
…
…
(
19
)
C
o
v
[
y
]
=
L
?
1
+
A
Λ
?
1
A
T
…
…
(
20
)
E[y]=A\mu+b\dots\dots(19)\\ Cov[y]=L^{-1}+A\Lambda^{-1}A^T\dots\dots(20)
E[y]=Aμ+b……(19)Cov[y]=L?1+AΛ?1AT……(20)
3.高斯过程回归的权空间观点推导
首先回想一般的线性回归模型,我们先不引入基函数,
y
=
x
T
w
+
?
y=x^Tw+\epsilon
y=xTw+?
其中
y
,
e
p
s
i
l
o
n
y,epsilon
y,epsilon是一维变量,代表实际数据值,
?
\epsilon
?表示高斯噪声,我们假设
?
~
G
a
u
s
s
i
a
n
(
?
∣
0
,
σ
n
2
)
\epsilon \sim Gaussian(\epsilon|0, \sigma_n^2)
?~Gaussian(?∣0,σn2?)
因此,由于训练样本
x
x
x是确定量,则
y
∣
w
,
x
~
G
a
u
s
s
i
a
n
(
y
∣
x
T
w
,
σ
n
2
)
y|w,x \sim Gaussian(y|x^Tw, \sigma_n^2)
y∣w,x~Gaussian(y∣xTw,σn2?)
下面规定
Y
Y
Y为实际数据值组成的向量,
X
X
X为输入
x
x
x组成的矩阵,这里我们反常的规定
X
X
X的每一列为一个输入,样本为
{
(
x
i
,
y
i
)
,
i
=
1
,
2
,
…
n
}
,
其
中
x
i
为
N
维
向
量
\{(x_i,y_i),i=1,2,\dots n \},其中x_i为N维向量
{(xi?,yi?),i=1,2,…n},其中xi?为N维向量
我们先做出
w
w
w的先验分布假设,设
w
~
G
a
u
s
s
i
a
n
(
w
∣
0
,
Σ
p
)
…
…
(
21
)
w \sim Gaussian(w|0, \Sigma_p)\dots\dots(21)
w~Gaussian(w∣0,Σp?)……(21)
Y的似然函数为
p
(
Y
∣
w
,
X
)
=
∏
i
n
p
(
y
i
∣
w
,
x
i
)
=
G
a
u
s
s
i
a
n
(
Y
∣
X
T
w
,
σ
n
2
I
)
…
…
(
22
)
p(Y|w, X)=\prod_{i}^np(y_i|w,x_i)=Gaussian(Y|X^Tw,\sigma_n^2I)\dots\dots(22)
p(Y∣w,X)=i∏n?p(yi?∣w,xi?)=Gaussian(Y∣XTw,σn2?I)……(22)
根据贝叶斯定理以及式(19)(20)可得
w
w
w的后验分布
w
∣
Y
,
X
~
G
a
u
s
s
i
a
n
(
w
∣
σ
n
?
2
A
?
1
X
Y
,
A
?
1
)
w|Y,X \sim Gaussian(w|\sigma_n^{-2}A^{-1}XY,A^{-1})\\
w∣Y,X~Gaussian(w∣σn?2?A?1XY,A?1)
其
中
A
=
Σ
p
?
1
+
σ
n
?
2
X
X
T
其中A=\Sigma^{-1}_p+\sigma_n^{-2}XX^T
其中A=Σp?1?+σn?2?XXT
得到
w
w
w的后验分布之后,我们需要进行预测,即得到预测分布,给定测试样本
(
X
?
,
Y
?
)
(X_*, Y_*)
(X??,Y??),我们仍考虑测试样本点带有高斯噪声的情况。从根本上来说,我们最终想得到的不是带有噪声的样本值,而是得到生成这些数据的函数,这也符合定义中所述:高斯过程是一个定义在函数上的分布。假设预测的函数为
f
?
f_*
f??,
则
p
(
f
?
∣
X
?
,
X
,
Y
)
=
∫
p
(
f
?
∣
X
?
,
w
)
p
(
w
∣
X
,
Y
)
d
w
p(f_*|X_*,X,Y)=\int p(f_*|X_*,w)p(w|X,Y)dw
p(f??∣X??,X,Y)=∫p(f??∣X??,w)p(w∣X,Y)dw
f
?
∣
X
?
,
w
~
G
a
u
s
s
i
a
n
(
f
?
∣
X
?
T
w
,
σ
n
2
I
)
f_*|X_*,w\sim Gaussian(f_*|X_*^Tw,\sigma_n^2I)
f??∣X??,w~Gaussian(f??∣X?T?w,σn2?I)
这同样是一个线性高斯模型,我们需要求解边缘概率分布,由式(19)(20)可得
f
?
∣
X
?
,
X
,
Y
~
G
a
u
s
s
i
a
n
(
f
?
∣
σ
n
?
2
X
?
T
A
?
1
X
Y
,
X
?
T
A
?
1
X
?
)
f_*|X_*,X,Y\sim Gaussian(f_*|\sigma_n^{-2}X_*^TA^{-1}XY,X_*^TA^{-1}X_*)
f??∣X??,X,Y~Gaussian(f??∣σn?2?X?T?A?1XY,X?T?A?1X??)
其中
A
=
Σ
p
?
1
+
σ
n
?
2
X
X
T
A=\Sigma^{-1}_p+\sigma_n^{-2}XX^T
A=Σp?1?+σn?2?XXT
接下来,我们引入基函数,用基函数
?
(
.
)
\phi(.)
?(.)将样本输入
x
i
x_i
xi?映射到高维特征空间,用
?
(
x
i
)
或
?
i
\phi(x_i)或\phi_i
?(xi?)或?i?来表示映射后的特征向量(feature vector,与eigenvector区分),用
Φ
\Phi
Φ表示特征向量组成的矩阵。
则
f
?
∣
X
?
,
X
,
Y
~
G
a
u
s
s
i
a
n
(
f
?
∣
σ
n
?
2
Φ
?
T
A
?
1
X
Y
,
Φ
?
T
A
?
1
Φ
?
)
…
…
(
23
)
f_*|X_*,X,Y\sim Gaussian(f_*|\sigma_n^{-2}\Phi_*^TA^{-1}XY,\Phi_*^TA^{-1}\Phi_*)\dots\dots(23)
f??∣X??,X,Y~Gaussian(f??∣σn?2?Φ?T?A?1XY,Φ?T?A?1Φ??)……(23)
其中
A
=
Σ
p
?
1
+
σ
n
?
2
Φ
Φ
T
…
…
(
24
)
A=\Sigma^{-1}_p+\sigma_n^{-2}\Phi\Phi^T\dots\dots(24)
A=Σp?1?+σn?2?ΦΦT……(24)
但是显示表示一个合适的基函数(basis function)不是一件容易的事情,更别说加上一个先验的协方差矩阵,因此我们隐式的引入这一式子。
我们设
K
=
Φ
T
Σ
p
Φ
K=\Phi^T\Sigma_p\Phi
K=ΦTΣp?Φ,我们先对式(24)进行处理。
等式两边同时左乘
A
?
1
A^{-1}
A?1,右乘
Σ
p
Φ
\Sigma_p\Phi
Σp?Φ,进行整理并带入
K
K
K可得
A
?
1
Φ
=
σ
n
2
Σ
p
Φ
(
σ
n
2
I
+
K
)
?
1
…
…
(
25
)
A^{-1}\Phi=\sigma_n^{2}\Sigma_p\Phi(\sigma_n^{2}I+K)^{-1}\dots\dots(25)
A?1Φ=σn2?Σp?Φ(σn2?I+K)?1……(25)
将(25)式代入(23)的均值部分可得,
E
[
f
?
]
=
Φ
?
T
Σ
p
Φ
(
σ
n
2
I
+
K
)
?
1
Y
E[f_*]=\Phi_*^T\Sigma_p\Phi(\sigma_n^{2}I+K)^{-1}Y
E[f??]=Φ?T?Σp?Φ(σn2?I+K)?1Y
利用矩阵求逆引理(6)可得
A
?
1
A^{-1}
A?1并带入(23)的协方差部分,可得
C
o
v
[
f
?
]
=
Φ
?
T
Σ
p
Φ
?
?
Φ
?
T
Σ
p
Φ
(
σ
n
2
I
+
K
)
?
1
Φ
T
Σ
p
Φ
?
Cov[f_*]= \Phi_*^T\Sigma_p\Phi_*-\Phi_*^T\Sigma_p\Phi(\sigma_n^{2}I+K)^{-1}\Phi^T\Sigma_p\Phi_*
Cov[f??]=Φ?T?Σp?Φ???Φ?T?Σp?Φ(σn2?I+K)?1ΦTΣp?Φ??
最后,我们引入核函数这个概念,设核函数
K
(
X
,
X
)
=
Φ
T
Σ
p
Φ
K(X,X)=\Phi^T\Sigma_p\Phi
K(X,X)=ΦTΣp?Φ,
以此类推,
K
(
X
?
,
X
)
=
Φ
?
T
Σ
p
Φ
K(X_*,X)=\Phi_*^T\Sigma_p\Phi
K(X??,X)=Φ?T?Σp?Φ,
K
(
X
?
,
X
?
)
=
Φ
?
T
Σ
p
Φ
?
K(X_*,X_*)=\Phi_*^T\Sigma_p\Phi_*
K(X??,X??)=Φ?T?Σp?Φ??
我们这里介绍常用的高斯核函数 k ( x , x ′ ) = σ 2 e x p { ∣ x ? x ′ ∣ 2 l } k(x,x')=\sigma^2 exp\{\frac{|x-x'|^2}{l}\} k(x,x′)=σ2exp{l∣x?x′∣2?},其中 l l l是高斯过程的length-scale,这里不做过多解释。
最后的形式为
E
[
f
?
]
=
K
(
X
?
,
X
)
(
σ
n
2
I
+
K
(
X
,
X
)
)
?
1
Y
E[f_*]=K(X_*,X)(\sigma_n^{2}I+K(X,X))^{-1}Y
E[f??]=K(X??,X)(σn2?I+K(X,X))?1Y
C
o
v
[
f
?
]
=
K
(
X
?
,
X
?
)
?
K
(
X
?
,
X
)
(
σ
n
2
I
+
K
(
X
,
X
)
)
?
1
K
(
X
,
X
?
)
Cov[f_*]= K(X_*,X_*)-K(X_*,X)(\sigma_n^{2}I+K(X,X))^{-1}K(X,X_*)
Cov[f??]=K(X??,X??)?K(X??,X)(σn2?I+K(X,X))?1K(X,X??)
至此,权空间视角的推导过程就结束了。
下面是python实现代码:
gaussian_process_regression.py
import numpy as np
class GaussianProcessRegressor:
"""
kernel: RBF(sigma_overall, l_scale)
alpha: noise, 1-D array or scaler
"""
def __init__(self, kernel, sigma_overall, l_scale, alpha=0.):
self.kernel = kernel(sigma_overall, l_scale)
self.alpha = alpha
def fit(self, X, y):
X = np.asarray(X)
y = np.asarray(y)
self.train_x_ = X
self.train_y_ = y
def predict(self, X, return_cov=True, return_std=False):
if return_cov and return_std:
raise RuntimeError("return_cov, return_std can't be True in the same time")
if not hasattr(self, 'train_x_'):
y_mean = np.zeros(X.shape[0])
if return_cov:
y_cov = self.kernel(X, X)
return y_mean, y_cov
elif return_std:
y_cov = self.kernel(X, X)
return y_mean, np.sqrt(np.diag(y_cov))
else:
return y_mean
K = self.kernel(self.train_x_, self.train_x_)
L = np.linalg.cholesky(K + self.alpha * np.eye(self.train_x_.shape[0]))
alpha = np.linalg.solve(L, self.train_y_)
alpha = np.linalg.solve(L.T, alpha)
y_mean = self.kernel(self.train_x_, X).T @ alpha
v = np.linalg.solve(L, self.kernel(self.train_x_, X))
y_cov = self.kernel(X, X) - v.T @ v + self.alpha * np.eye(X.shape[0])
if return_cov:
return y_mean, y_cov
elif return_std:
return y_mean, np.sqrt(np.diag(y_cov))
else:
return y_mean
def sample_func(self, X, n_samples=1):
y_mean, y_cov = self.predict(X, return_cov=True, return_std=False)
sampled_y = np.random.multivariate_normal(y_mean, y_cov, size=n_samples)
return sampled_y
kernel.py
import numpy as np
class RBFKernel:
def __init__(self, sigma, scale):
self.sigma = sigma
self.scale = scale
def __call__(self, x1: np.ndarray, x2: np.ndarray):
m, n = x1.shape[0], x2.shape[0]
K_matrix = np.zeros((m, n), dtype=float)
for i in range(m):
for j in range(n):
K_matrix[i, j] = self.sigma * np.exp(-0.5 * np.sum((x1[i] - x2[j]) ** 2) / self.scale)
return K_matrix
测试代码:
from gaussian_process import RBFKernel, GaussianProcessRegressor
import numpy as np
import matplotlib.pyplot as plt
def get_y(x, alpha):
return np.cos(x)*0.3 + np.random.normal(0, alpha, size=x.shape)
observation_size = 6
gpr = GaussianProcessRegressor(RBFKernel, sigma_overall=0.04, l_scale=0.5, alpha=1e-4)
sample_size = 3
test_x = np.linspace(0, 10, 100)
prior_mean, prior_cov = gpr.predict(test_x, return_cov=True)
sample_ys = gpr.sample_func(test_x, n_samples=sample_size)
uncertainty = 1.96 * np.sqrt(np.diag(prior_cov))
plt.plot(test_x, prior_mean, label='mean')
plt.fill_between(test_x, prior_mean-uncertainty, prior_mean+uncertainty, alpha=0.1)
for i in range(sample_size):
plt.plot(test_x, sample_ys[i], linestyle='--')
plt.legend()
plt.title('prior')
plt.show() # 至此绘制先验分布
train_x = np.array([3, 1, 4, 5, 7, 9])
train_y = get_y(train_x, alpha=1e-4)
gpr.fit(train_x, train_y)
y_mean, y_cov = gpr.predict(test_x, return_cov=True)
sample_ys = gpr.sample_func(test_x, n_samples=sample_size)
uncertainty = 1.96 * np.sqrt(np.diag(y_cov))
plt.plot(test_x, y_mean, label='mean', linewidth=3)
plt.fill_between(test_x, y_mean-uncertainty, y_mean+uncertainty, alpha=0.1)
for i in range(sample_size):
plt.plot(test_x, sample_ys[i], linestyle='--')
plt.scatter(train_x, train_y, c='red', marker='x', label='observation', linewidths=5)
plt.legend()
plt.title('posterior')
plt.show() # 绘制后验分布
运行效果如下
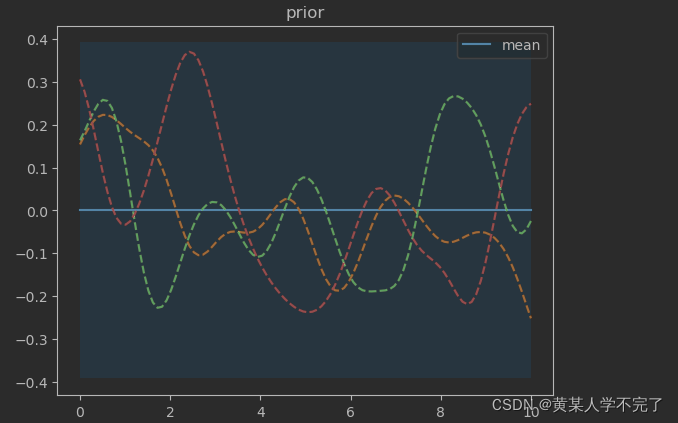

下次补充函数空间的观点。
本人大二,水平有限,若有不严谨之处,请见谅。
参考文献
[1]C. E. Rasmussen & C. K. I. Williams.(2006). Gaussian Processes for Machine Learning.7-29.
[2]Christopher M. Bishop.(2007). Pattern Recognition and Machine Learning. 78-93.