[人工智能]向量的1范数，2范数，无穷范数，KNN中的Lp距离

L-0范数：用来统计向量中非零元素的个数。
L-1范数：向量中所有元素的绝对值之和。
L-2范数：欧式距离。
L-∞范数：计算向量中的最大值。

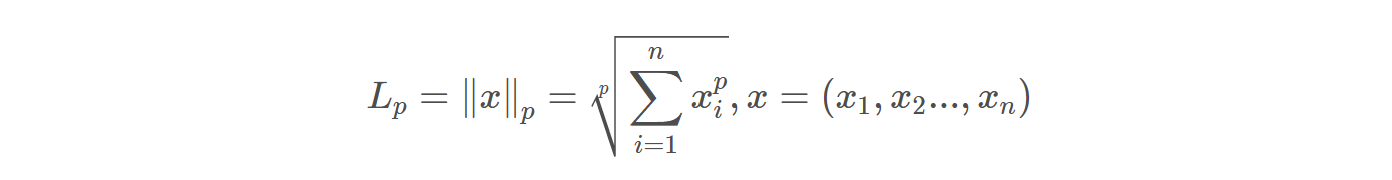
你也可以这样理解
1-范数：$║x{║}_1=│x^1│+│x^2│+\dots +│x^n│$
2-范数：
$║x{║}_2=\sqrt[2]{(│x^1{│}^2+│x^2{│}^2+\dots +│x^n{│}^2)}$
∞-范数：
$║x{║}_{\infty }=max（│x^1│，│x^2│，\dots ，│x^n│）$

看下面这组数A=(3,4,5)和B=(6,1,1)谁大?

用二范数$\sqrt[2]{A}=\sqrt[2]{50},\sqrt[2]{B}=\sqrt[2]{38},A>B$
但是如果用无穷范数比较:
||B||=6>||A||=5,所以不同的度量标准下数据的大小关系可能会发生变化

下面看看范数在KNN算法中的使用，一般的KNN算法使用欧氏距离作为距离度量，但是这种方式只适用于样本是球形簇的情况，比如下面这种情况就不适合欧式距离
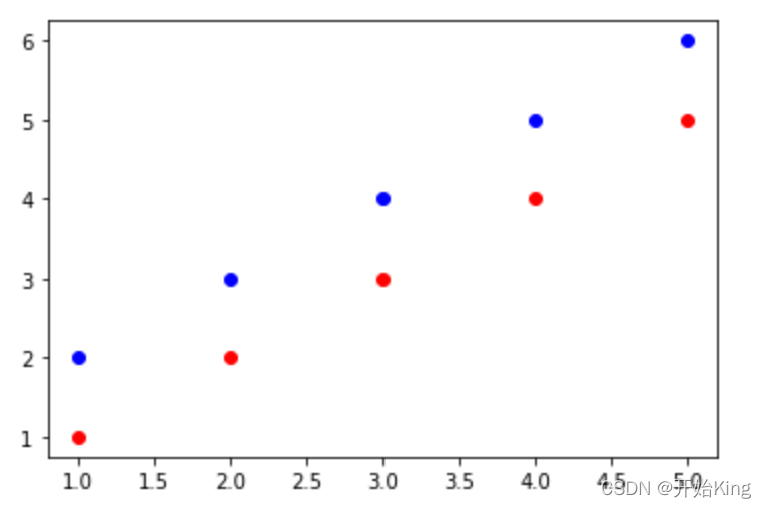因此可能会选用不同的距离定义
1 闵可夫斯基距离
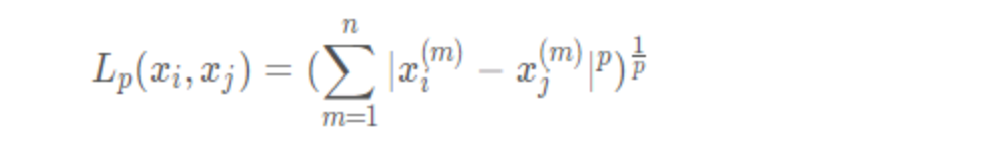$这里p?1$

2 曼哈顿距离$p=1$
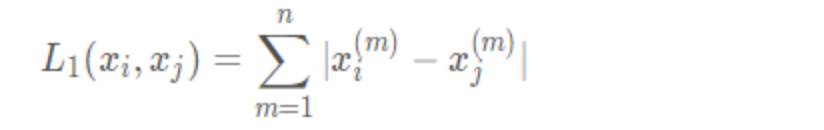3 欧式距离$p=2$

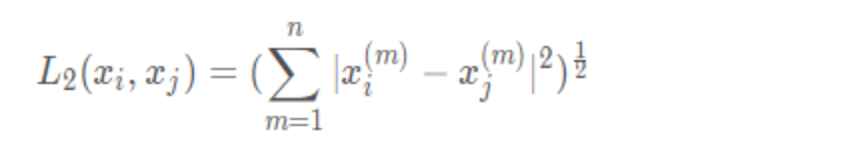
4 切比雪夫距离$p=\infty$

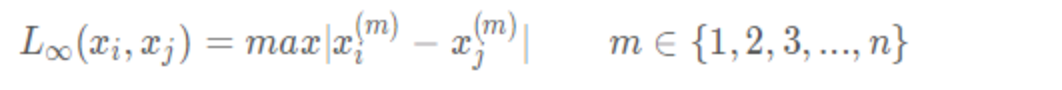
$x^m表示样本x的m个特征，x_i表示第i个样本，x_i^m表示第i个样本的第m个特征$